Предмет и задачи курса "Теория нечетких множеств". Общее применение нечетких моделей. Теория четких множеств. Теория нечетких множеств

В.З. Манусов

Теория нечетких множеств

Курс лекций для магистрантов и аспирантов факультета энергетики

Содержание:

Предмет и задачи курса……………………………………………….3

1. Общее применение нечетких моделей…………………………….6

   1.1. Основная сущность нечеткой методологии…………………..6

   1.2. Макрознания и макромодели…………………………………..8

   1.3. Человеко-машинные системы………………………………….9

   1.4. Нечеткие системы……………………………………………...10

   1.5. Природа и сущность субъективизма………………………….12

   1.6. Область применения нечетких моделей……………………...15

   1.7. Обсуждение результатов………………………………………16

2. Теория четких множеств…………………………………………..18

   2.1. Общие соображения…………………………………………...18

   2.2. Основные понятия и определения…………………………….18

   2.3. Общие законы теории четких множеств…………………......21

3. Теория нечетких множеств………………………………………..23

   3.1. Основные понятия и определения теории нечетких множеств………………………………………………………………23

   3.2. Построение функции принадлежности……………………….26

   3.3. Типичные (характерные) функции принадлежности………..31

   3.4. Алгебра нечетких множеств…………………………………..33

   3.5. Алгебра составных нечетких переменных…………………...37

   3.6. Основные принципы нечеткого управления…………………39

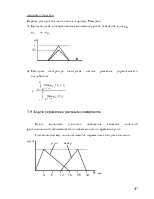
   3.7. Агрегация локальных выводов и дефаззификация…………..44

   3.8. Нечеткие алгоритмы управления……………………………..45

   3.9. Задача управления уличным освещением……………………47

Предмет и задачи курса

Познание природы человеком и в том числе познание самого человека (homo sapiens – человека разумного) привело к созданию новых наук. Для их создания необходимо:

·  наличие новых фактов;

·  общественное созревание, обусловленное необходимостью применения новых идей;

·  общественное признание этих идей.

С наступлением эры ЭВМ возникла проблема формализации не только описания самих технических систем, но и языка общения субъектов с этими ЭВМ.

Ранее устоявшееся представление, описание, изучение, исследование любых систем (механических, на основе электромагнетизма, электронных и др.) требовали их формального математического описания с возможностью получения некоторых численных результатов.

Однако с появлением гуманистических систем (человеко-машинных, эргатических) возникла сложная задача согласования мышления человека и его естественного языка с формальным языком компьютера. Эту задачу можно сформулировать так: необходимо выполнять вычисления не только с числами, но и со словами. Так как словесные выражения не являются четкими и достаточно размыты, это потребовало введения нечетких переменных и лингвистических переменных. Эти вычисления – Soft Computing ("Мягкие вычисления").

Все это породило создание в 1968 году новой науки – теории нечетких множеств (Fuzzy Sets, от англ. "fuzzy" – нечеткий). Ее автор – Лотфи Заде (Lotfi Zadeh).

С физической точки зрения "fuzzy" – нечеткий, пушистый – возникло на основе ворсистости ковра. Низ – ковер (четкое), вверху – воздух. Волоски ковра – еще не ковер, но уже и не воздух.

Таким образом, ключевой задачей теории нечетких множеств (ТНМ) является согласование естественного языка субъекта и формального языка компьютера.

Это обусловлено тем, что логическое и четкое численное решение опирается на левое полушарие человека, а образное и интуитивное – на правое.

В настоящее время компьютеры значительно превосходят по скорости вычислений и памяти мозг человека. Отсюда может создаться забавное впечатление, что машины якобы умнее людей, они работают как чисто левое полушарие. Однако основная смысловая нагрузка, отбор значимых и незначимых факторов, а также интуитивные позывы и импульсы человек получает из правого полушария. Именно оно лежит в основе творческого потенциала личности.

Таким образом, ТНМ направлена, прежде всего, на самого человека, моделирование его образа мыслей и в том числе здравого смысла.

Ключевым моментом ТНМ является переход к некоторым лингвистическим переменным, которые в свою очередь включают некоторое количество так называемых "термов" – нечетких переменных.

Пример: возраст – лингвистическая переменная, может состоять из следующих нечетких переменных:

·  очень молодой;

·  молодой;

·  более или менее молодой;

·  нестарый;

·  старый;

·  очень старый.

На этой основе в настоящее время разработаны fuzzy-технологии. Они основаны на нечетких правилах.

Пример: если X – большое, то y – маленькое.

Нечеткие понятия могут касаться как самой вероятности, так и понятия истинности.

Пример:

·  невероятно;

·  маловероятно;

·  более или менее вероятно;

·  достаточно вероятно;

·  очень вероятно.

Этим нечетким переменным можно подставить в соответствие некоторые значения вероятностей; но они будут разными у различных субъектов.

Таким образом, ТНМ в отличие от "чистой" математики отражает субъективную, индивидуальную вероятность.

Приложение ТНМ к истинности, а именно: очень истинно, истинно, достаточно истинно, 0, не знаю, достаточно ложно, ложно, абсолютная ложь; привело к созданию нечеткой логики – новой ветви ТНМ. Это привело к тому, что между истиной и ложью существуют промежуточные значения.

Пример: может быть – 70% истина, 30 % ложь (или 50/50, или др.)

Следовательно, ТНМ является мощным инструментом согласования естественного языка и представлений человека с формализованным машинным языком. Это же касается и систем управления, где положительные и отрицательные обратные связи заменяются нечеткими продукционными правилами. Все это в совокупности позволяет получить экономически целесообразные и высокопродуктивные решения.

1. Общее применение нечетких моделей

1.1. Основная сущность нечеткой методологии

Основная сущность новой методологии, построенной на нечетких множествах, состоит в необходимости формализации естественных знаний субъекта. С учетом субъективизма и смысловых оттенков любых значений.

Эта формализация осуществляется в математической форме исходя их некоторых исходных постулатов, которые, несмотря на некоторую расплывчатость, нечеткость, позволяют создать достаточно строгую теорию. Необходимость этого обусловлена существенным различием между естественным языком человека и "компьютерным" языком.

Эта задача составляет основную сущность нечеткой методологии, но не только она. Дело в том, что в отличие от четких множеств, опирающихся на двузначную логику, в нечетких моделях и рассуждениях понятие логики значительно усложняется.

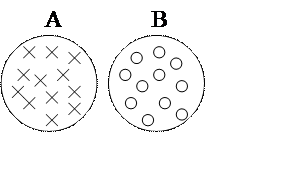
Различают три вида логических рассуждений, вытекающих из той или иной концепции четких и нечетких множеств:

1.