Рассмотрим 3 нечетких понятия – "начало/середина/конец недели". В принятых вербальных оценках содержится субъективное восприятие понятия "дата" относительно начала, середины или конца недели.
Переведем в функцию принадлежности:
|
Базовая переменная |
Начало |
Середина |
Конец |
|
|
Пн |
1,0 |
0 |
0 |
1,0 |
|
Вт |
0,6 |
0,2 |
0 |
0,8 |
|
Ср |
0 |
1,0 |
0 |
1,0 |
|
Чт |
0 |
0,6 |
0,3 |
0,9 |
|
Пт |
0 |
0 |
0,7 |
0,8 |
|
Сб |
0 |
0 |
0,9 |
0,9 |
|
Вс |
0 |
0 |
1,0 |
1,0 |
Тогда имеем следующие функции принадлежности:
Начало недели: 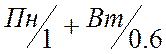
Середина недели: 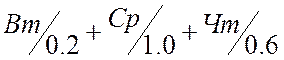
Конец недели: 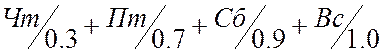
1) Сумма этих принадлежностей должна быть близка к 1 (в этом отличие от теории вероятностей).
2) Крайние значения (Пн: 1 – начало, 0 – конец; Вс: 1 – конец, 0 – начало) характеризуют Булеву алгебру как частный случай.
Таким образом, построение функции принадлежности опирается на вербальные оценки, "за кулисами" которых стоят численные оценки.
Рассмотрим лингвистическую переменную "интеллект". В этом случае человечеством предпринимаются попытки наряду с вербальными нечеткими переменными дать их численную оценку. Можно ввести следующие термы понятия "интеллект": сверходаренные (гении), одаренные, очень способные, способные, нормальные, малоспособные, дебилы, имбецилы (кретины), идиоты.
Данное терм-множество представляет собой набор нечетких понятий, входящих в лингвистическую переменную "интеллект". Их соответствие базовой переменной может быть сделано на основе коэффициента IQ (Intelligence Quotient):
Сверходаренные >160 пунктов
Одаренные 160 – 145
Очень способные 145 – 130
Способные 130 – 115
Нормальные 100 – 85
Малоспособные 85 – 70
Дебилы 70 – 55
Имбецилы 55 – 40
Идиоты 40 – 25
Таким образом, в данном случае эту модель можно развить путем построения функции принадлежности относительно какого-либо субъекта.
Опираясь на статистический закон распределения, можно предположить, что принадлежность некоторого субъекта к нечеткому понятию "нормальный" составляет ≈0,7. Также можно предположить, что в данной аудитории остальные значения принадлежности будут относиться к нечетким понятиям "способный", "очень способный", "одаренный".
Рассмотрим также функцию принадлежности для лингвистической переменной "езда на автомобиле". Выше было выбрано терм-множество для этой цели.

стоп
очень медленно
медленно
нормально
быстро
очень быстро
сверхбыстро
Из этого терм-множества следует, что любая скорость может быть отнесена к разным нечетким переменным:
80 км/ч принадлежит с принадлежностью 0,8 к нормальной езде и с принадлежностью 0,4 к быстрой езде.
Таким образом, с помощью функции принадлежности и, главным образом, некоторого терм-множества – набора функций принадлежности – можно оценить пересечение различных классов множеств, и на этой основе оценить состояние элемента, а именно: на сколько он принадлежит тому или иному классу множеств.
В этом состоит главный постулат теории нечетких множеств: элемент может принадлежать разным множествам одновременно с различной степенью принадлежности.
3.3. Типичные (характерные) функции принадлежности
В инженерной практике и научных исследованиях установились некоторые традиции отображения реальных процессов с помощью функции принадлежности. При этом различают как бы дуальные функции принадлежности либо как гладкие функции, либо как набор линейных функций:
1) Монотонно возрастающие функции
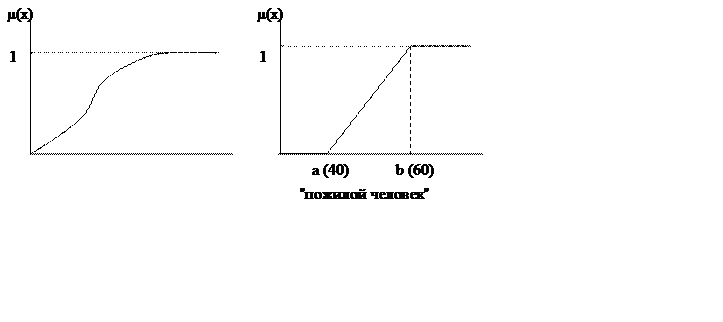
2) Монотонно убывающие функции

3) Функции принадлежности как треугольное распределение (характеризует: около, приблизительно, почти)

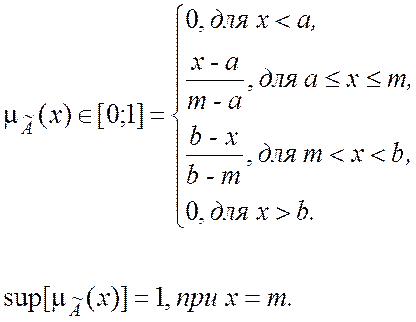
Таким
образом, максимальное значение функции принадлежности соответствует m.
Восходящая ветвь описывается 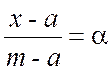 – коэффициент восхождения,
нисходящая ветвь описывается
– коэффициент восхождения,
нисходящая ветвь описывается 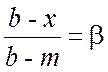 – коэффициент нисхождения.
– коэффициент нисхождения.
4) Нечеткий интервал
Характеризуется нечеткими границами интервала (a; b)

Углы наклона трапеции определяются теми же выражениями, что и для треугольной функции.
Другой способ состоит в представлении границ как гауссовских кривых:
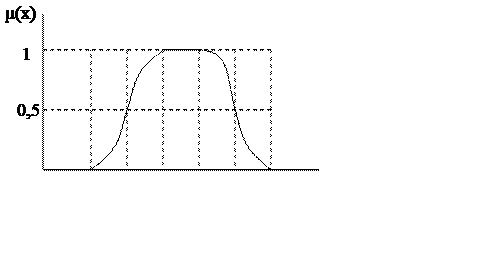
Например, качество электрической энергии. Функция принадлежности отклонения напряжения может быть представлена нечетким интервалом.
Допустимые интервалы
(вероятность 0,95): ± 5% ![]()
Допустимые интервалы
(вероятность 0,05): ± 10% ![]()
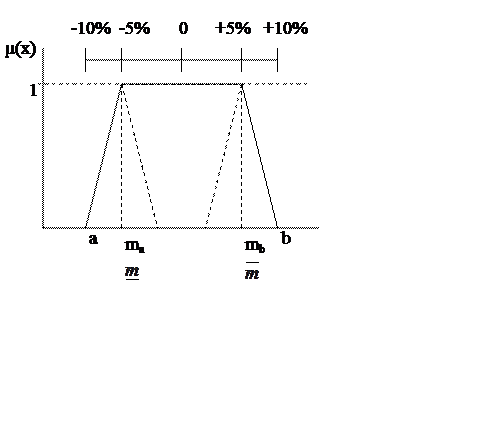
3.4. Алгебра нечетких множеств
Алгебра нечетких множеств (АНМ) отличается от алгебры четких множеств и алгебры событий в теории вероятностей. Реально АНМ предполагает операции с функциями принадлежностей. Однако сами операции записываются как операции с нечеткими множествами.
Различают следующие действия:
1) Эквивалентность
![]() .
.
Все пары чисел для функции принадлежности имеют одинаковые значения принадлежностей.
2) Включение (вложение)
![]() .
// A влечет за
собой B
.
// A влечет за
собой B

3) Дополнение
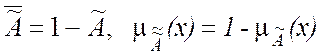 .
.
Дополняет функцию принадлежности до множества, имеющего функцию принадлежности, равную 1.
Позволяет получить обратное нечеткое множество. В вербальных моделях дополнение следует рассматривать как отрицание прямого утверждения.
Пример: молодой, не молодой;
давно, не давно́.
4) Объединение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.