· очень низкий
Если уровень высокий, то открыть кран.
,
.
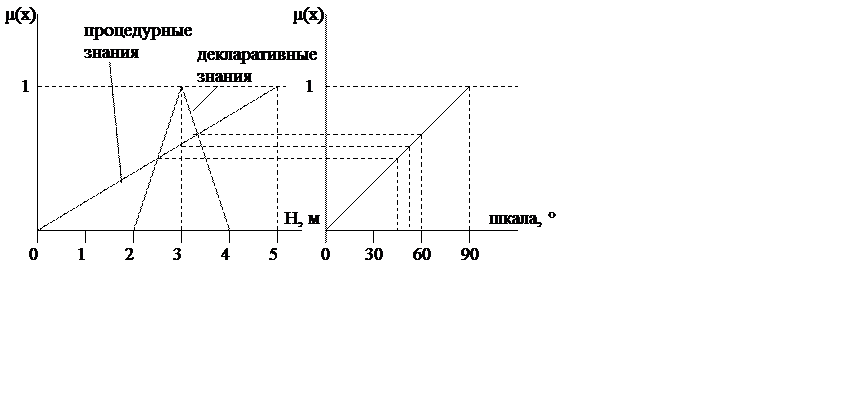
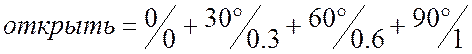Пусть уровень около 3 м. Если уровень высокий, то кран приоткрыть (45°÷60°), затем берем центр тяжести фигуры – 52°÷55°.
Для управления по правилам нужны просто алгебраические операции с нечеткими переменными, нет необходимости в построении обратной связи.
В реальной жизни нечеткий логический вывод выполняется с помощью нечетких контроллеров, а сама единица измерения называется FLIPS.
Сейчас скорость выполнения операции FLIPS – время, за которое световой луч или электромагнитная волна проходит 7,5 метров в вакууме.
Например, в японском метрополитене позволяет вести управление поездом с точностью до 3 сек.
Кроме рассмотренных ранее функций принадлежности относительно одного терм-множества существуют также функции принадлежности двух, трех и более терм-множеств. Такие функции принадлежности описывают многомерное множество и носят название "нечеткие отношения".
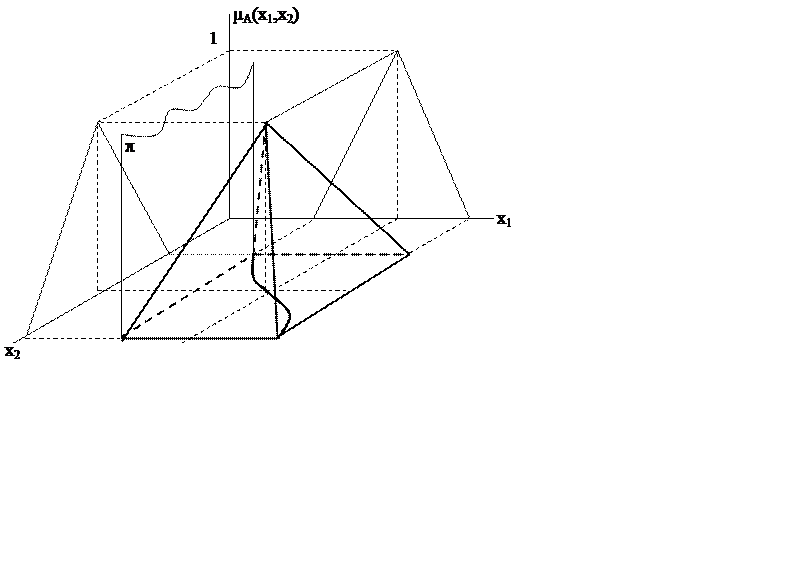
По классическому определению нечетким отношением называется соответствие точки x1 из множества A1 точке x2 из множества A2 со степенью принадлежности μ (x1, x2).
Классическими примерами функции принадлежности являются функции пирамидального типа:
,
а также функции колоколообразного типа:
.
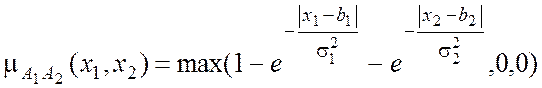Пример: найдем с помощью нечетких отношений нечеткое значение ≈5+≈3
Для решения данной задачи предпримем следующие действия:
1) Зафиксируем x1=3
Построим в плоскости μx2 вспомогательную плоскость π. Отобразим изокривые на плоскости x1, x2.
2) x1=4 → μ=1/2
3) x1=5 → μ=1
4) x1=6 → μ=1/2
5) x1=7 → μ=0
Далее по аналогии с рассмотренными пятью пунктами строится плоскость π, описываемая x2=const, и проводятся аналогичные построения.
,
x1+ x2=8,
x1+ x2=6,5,
x1+ x2=9,5,
x1+ x2=5,
x1+ x2=11.
Изобразим функцию принадлежности нечеткой суммы ≈5+≈3:
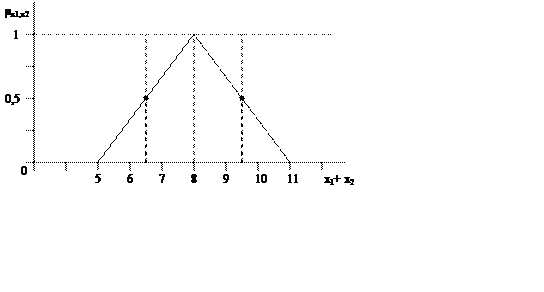
Данный рассмотренный пример одинаково справедлив для процедуры умножения, деления, вычитания.
3.7. Агрегация локальных выводов и дефаззификация
Механизм нечеткого логического вывода выглядит следующим образом:
Методы агрегации:
1) На основании приведенной схемы,
получаемой из базы правил, нечеткие локальные выводы преобразуются в
генеральные нечеткие решения (
). Далее
дефаззифицируются в их четкие значения.
2) Полученные из базы правил, нечеткие локальные выводы обрабатываются при помощи алгоритмов Мамдани (Mamdani), Сугено (Sugeno), Ларсена (Larsen), Цукамото (Tsukamoto), Ягера (Yager) и др.
3.8. Нечеткие алгоритмы управления
Алгоритм Мамдани
Выполняется в несколько этапов.
1) Отыскиваются соответствующие для каждого правила функции принадлежности предложений-предпосылок.
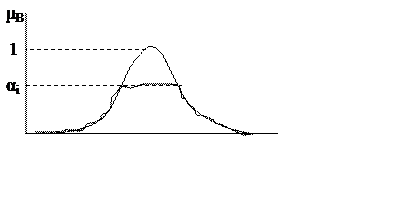
2) Находятся уровни отсечения для каждого правила (α-уровни)
3) Производится операция логического умножения соответствующего α-уровня и функции принадлежности вывода
|
4) Дефаззификация методом центра масс (центроида; взвешенного среднего)
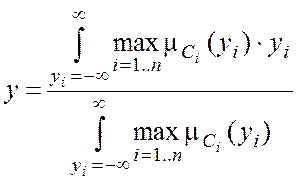
Алгоритм Цукамото
Первые два пункта аналогичны алгоритму Мамдани.
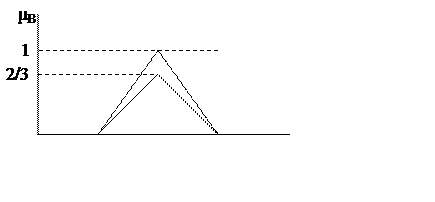
3) Предполагается, что функции принадлежности выводов являются монотонными.
4) αi приравнивается функции принадлежности μBi
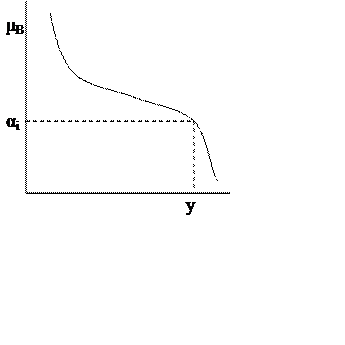
Находится соответствующее четкое значение y для каждого из правил.
5) Методом центроида (или другим методом дефаззификации) отыскивается средневзвешенное управляющее воздействие
Алгоритм Сугено нулевого порядка
Если x1 есть A1 и x2 есть A2, тогда y есть Ci
Первые два пункта аналогичны алгоритму Мамдани.
3) Методом центроида находится управляющее воздействие
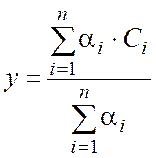, Ci =const
Алгоритм Сугено первого порядка
Если x1 есть A1 и x2 есть A2, тогда y есть Ci= aix1+ bix2+k
Первые два пункта аналогичны алгоритму Мамдани.
3) Находятся индивидуальные выходы из правил
Ci*= aix01+ bix02+k
4) Методом центроида находится четкое решение управляющего воздействия.
Алгоритм Ларсена
Первые два пункта аналогичны алгоритму Мамдани.
3) Производится алгебраическое умножение уровня отсечения αi на μBi
|
4) Методом центроида находится четкое решение управляющего воздействия
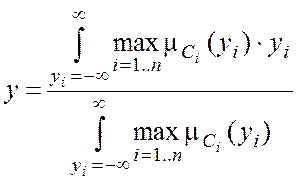
3.9. Задача управления уличным освещением
Пусть мощность уличного освещения является нечеткой функциональной зависимостью от освещенности и времени суток.
Составим систему лингвистических переменных входных величин:
|
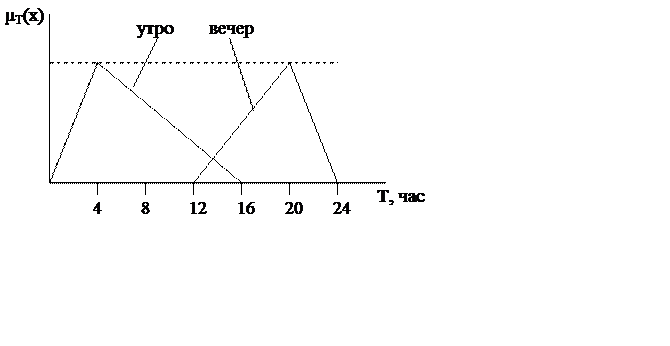
Освещенность |
Время |
|
|
утро |
вечер |
|
|
темно |
малая |
полная |
|
сумерки |
нулевая |
средняя |
|
светло |
нулевая |
малая |
База правил составляется экспертным путем. База правил может быть составлена с помощью обучающей выборки (то есть некоторой системы заведомо правильных адекватных решений), а также экспертно (то есть на личном опыте человека).
Покажем решение данной задачи с применением некоторых алгоритмов нечеткой логики.
1. Алгоритм Мамдани
Пусть T=4 часа утра, A=20 люкс.
Находим уровни отсечения для каждого из правил.
2. Алгоритм Ларсена
Пусть T=10 часа утра, A=5 люкс.
Так как принадлежность 0,5, то функция принадлежности уменьшается в 2 раза.
По методу центроида управляющее воздействие определяет заштрихованная площадка.
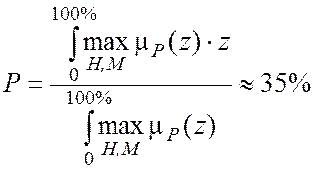
3. Алгоритм Цукамото
Пусть T=10 часа утра, A=5 люкс.
4. Алгоритм Сугено нулевого порядка
Пусть T=10 часа утра, A=5 люкс.
zМ=25, zН=0, zС=75, zП=100.
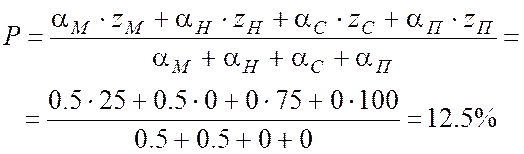
5. Алгоритм Сугено первого порядка
Пусть T=10 часа утра, A=5 люкс.
zМ=0,3x+0,7y+10,
zН=0,1x+0,3y+0,
zС=0,6x+0,9y+20,
zП=0,8x+0,7y+30.
x→T, y→A
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.