Предмет и задачи курса "Теория нечетких множеств". Общее применение нечетких моделей. Теория четких множеств. Теория нечетких множеств, страница 5

Итак, в теории множеств возможная дуальная запись всех законов. Ни одна из этих форм не имеет преимущества перед другой и отражает только эстетические вкусы автора. Под дуальностью понимается зеркальное отображение – пересечение и объединение. При этом следует иметь в виду, что в общей теории множеств основным исходным постулатом слежит определение, что элемент множества x может принадлежать или не прнадлежать множеству X. То есть ответ на этот вопрос – да или нет (или с точки зрения Булевой алгебры – 0 или 1).

3. Теория нечетких множеств

3.1. Основные понятия и определения теории нечетких множеств

Как и любая наука, ТНМ опирается на некоторые понятия и определения. Главным из них является понятие лингвистической переменной и функции принадлежности.

Под лингвистической переменной понимается переменная, значениями которой являются не цифры, не численные значения, а слова или предложения.

Между тем, за этими вербальными значениями, "за кулисами", обычно скрываются некоторые численные значения.

Замечание: Однако в реальной действительности за лингвистической переменной не всегда стоят численные значения. Например, красота или истинность.

Лингвистические переменные (например, зарплата, возраст или температура) могут быть разбиты на некоторое количество термов – терм-множеств. По Саати их должно быть 3, 5, 7 или 9.

Примеры:   зарплата – высокая, средняя, низкая;

температура – очень горячая, горячая, нейтральная, холодная, очень холодная;

напряжение – сверхвысокое, высокое, нормальное, низкое, очень низкое;

ветер – штиль, очень слабый, слабый, нормальный, средний, сильный, очень сильный, шторм, ураган.

Таким образом, лингвистическая переменная с помощью терм-множеств может включать в себя несколько нечетких переменных, которые и составляют основу терм-множеств.

Выбор числа и свойств нечетких переменных относится к искусству автора. Количество нечетких переменных определяется так называемым синтаксисом лингвистической переменной, а их прагматический смысл – семантикой лингвистической переменной.

Вторым важным компонентом является функция принадлежности (membership). Она является некоторой моделью (объектом-заместителем) описания в нечетком мире. При этом базовая переменная (например, возраст, интеллект) может содержать некоторые смысловые оттенки, семантика которых может быть выражена с помощью функции принадлежности.

Множества в ТНМ обозначаются заглавными латинскими буквами с "волной": .

,

где μ(x) – степень принадлежности данного элемента к данному множеству.

Эта степень отражается на шкале от 0 до 1, где 0 означает абсолютную непринадлежность, а 1 – абсолютную принадлежность. И в этом случае непрерывная логика Заде вырождается в Булеву алгебру.

Пример: рассмотрим продолжение примера.

               0, 1, 2, 3, 4, 5, 6, 7, 8, 9

               A = {0, 2, 4, 6, 8}  #=5

                    B = {1, 3, 5, 7, 9}  #=5

                    .

Рассмотрим понятие "малое число". Какое число можем считать малым, а какое нет? Это понятие является нечетким, так как определяется субъективизмом.

.

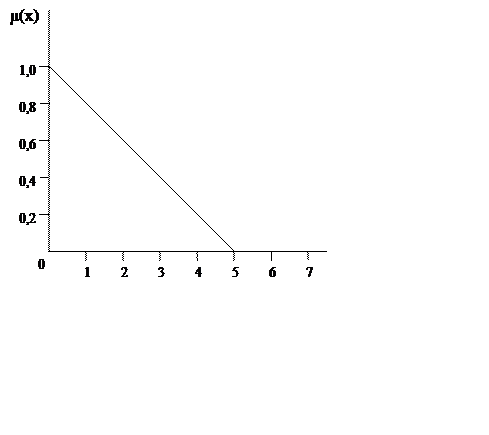
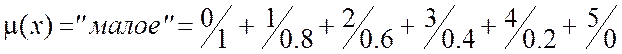Таким образом, функция принадлежности выражается некоторым рядом, состоящим из пар чисел: в числителе пишется само число, а в знаменателе – его принадлежность к данному множеству. "+" означает не суммирование, а объединение! (см. теорию четких множеств). Элементы с принадлежностью 0 принято не записывать. Функция принадлежности имеет такой вид, так как этого захотел автор.

Наряду с этим есть его функция принадлежности, ее функция принадлежности, их функция принадлежности, ибо функция принадлежности есть отражение субъективизма.

Эта функция имеет важное преимущество в том, что обеспечивает плавный переход от одного терма к другому, и тем самым обеспечивает "мягкое" регулирование и "мягкое" толкование лингвистических переменных.

Возраст:

Функция принадлежности в самом общем случае может быть с принадлежностью больше 1, однако в ТНМ любую функцию принадлежности принято нормировать. Это означает, что максимальное значение принадлежности не может быть больше 1.

3.2. Построение функции принадлежности

Построение функции принадлежности является первоочередной и ключевой задачей нечетких моделей. В настоящее время не существует точных рекомендаций, как построить функцию принадлежности. Различают два больших класса: прямые методы построения и косвенные.

Прямые методы основаны на субъективном восприятии процесса или явления и выражаются непосредственно субъектом.

Пример: для скорости автомобиля 0 – 200 км/ч

стоп, очень медленно, медленно, нормально, быстро, очень быстро, сверхбыстро.

Косвенные методы обычно основаны на некоторых статистиках и являются обобщением или сглаживающей кривой гистограммы. Сюда же относится выбор функции принадлежности через отношения.

Пример: этот в 2 раза сильнее того

Различают функции принадлежности монотонно убывающие, монотонно возрастающие, треугольные, трапецеидальные, основанные на нормальном распределении.

Конкретные функции распределения в этом случае рассмотрим позже в форме нечеткого интервала, так как они являются непрерывными.

Более распространенным является представление функции принадлежности для нечетких понятий в форме некоторых дискретных значений.

Пример: рассмотрим функцию принадлежности для нечеткого понятия "день недели".

Базовое значение	Неприменимо	Возможно	Допустимо	Соответствует
Пн	середина конец	нет	нет	начало
Вт	конец	середина	начало	нет
Ср	начало конец	нет	нет	середина
Чт	начало	конец	середина	нет
Пт	начало середина	конец	конец	нет
Сб	начало середина	нет	конец	конец
Вс	начало середина	нет	нет	конец