Анализ влияния уравнительных токов на технико-экономические показатели системы тягового электроснаб­жения, страница 3

Из анализа этих зависимостей видно, что даже при отсутст­вии нагрузки в плечах тяговой сети уравнительный ток в зави­симости от транзита мощности по ЛЭП, достигает значительной величины.

Включение устройств продольной емкостной компенсации изменяет величину 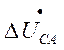  и 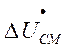 и уменьшает сопротивление контура . При этом составляющая уравнительного тока, обусловленная транзитом мощности по ЛЭП, всегда увеличивается, а две другие составляющие в зависимости от степени компенсации могут как увеличиваться так и уменьшаться.

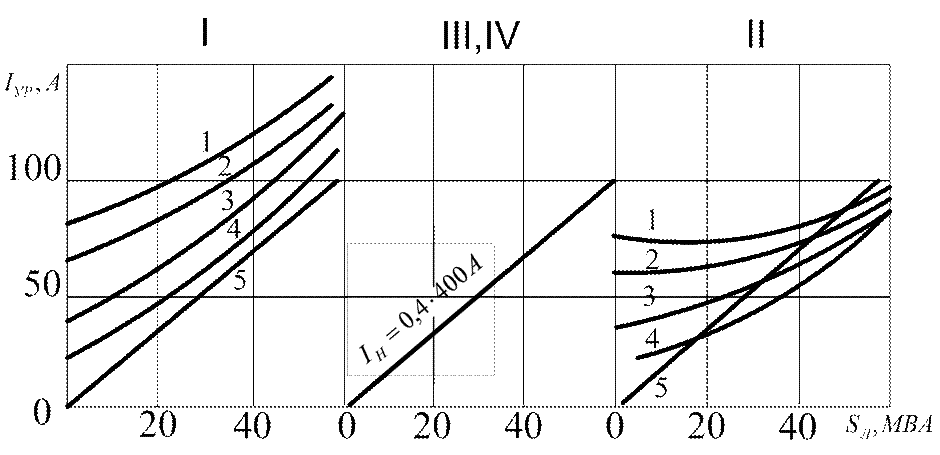
Рисунок 3.5-Зависимости уравнительного тока от тяговой нагрузки и транзита мощности по ЛЭП

3.2 Определение величины уравнительного тока в тяговой сети по счетчикам подстанций

Величина уравнительного тока в тяговой сети, вызываемого разностью напряжений смежных тяго­вых подстанций, зависит от многих факторов, наи­более существенными из которых являются конфи­гурация и режимы работы системы внешнего элек­троснабжения. Эти факторы трудно поддаются рас­четам и требуют исходных данных, которыми желез­нодорожные организации не располагают. Поэтому более надежным является непосредственное опреде­ление уравнительного тока на действующих участках.

Достаточно простым способом определения уравнительного тока является его измерение в мо­менты отсутствия на межподстанционной зоне тяго­вой нагрузки. Но такие периоды бывают не на всех зонах.

Предложены и другие способы определения урав­нительного тока: по отсутствию третьей гармони­ческой составляющей в токе плеча питания (уравни­тельный ток практически синусоидален); с по­мощью специализированного измерительно-вычис­лительного комплекса (ОмГУПС); посредством установки приборов контроля действующих значе­ний напряжений и токов на смежных подстанциях (МГУПС).

Однако все эти способы измерения уравнитель­ного тока требуют применения специализированно­го оборудования, которое в настоящее время серий­но не выпускается.

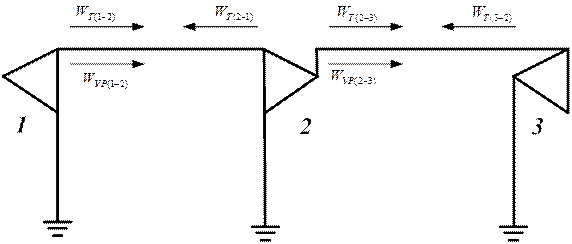
Рисунок 3.6- Схема с тремя подстанциями и двумя межподстанционными

зонами

Ниже изложена расчетно-экспериментальная ме­тодика определения уравнительного тока, основан­ная на использовании показаний счетчиков элек­трической энергии подстанций и расчетов распреде­ления токов нагрузки по подстанциям и плечам пи­тания.

Принцип методики состоит в следующем. Для участка, например, с тремя тяговыми подстанциями (рисунок 3.6) составляется система уравнений отдельно для расходов активной и реактивной энергии (при большем количестве подстанций число уравнений соответственно увеличивается). Учитывая, что актив­ные составляющие расходов электроэнергии на тягу и от уравнительного тока можно складывать арифме­тически (как и реактивные составляющие), то

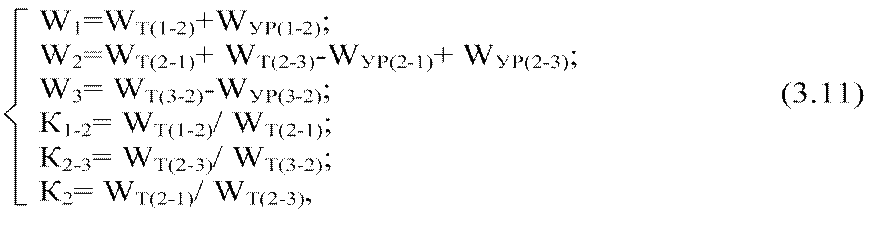
где W₁, W₂, W₃— расход энергии по трехфазным счетчикам тяговых подстанций; К_1-2, К_2-3— коэффициен­ты распределения расхода электроэнергии на тягу по подстанциям и при движении ЭПС по соответ­ствующим межподстаниионным зонам;

 К₂— коэф­фициент распределения расхода электроэнергии подстанции 2 по плечам питания (при отсутствии уравнительного тока); остальные обозначения по­нятны из рисунок 3.6

Для определения коэффициентов К_1-2, К_2-3 и К₂ на основе тягового расчета или опытных поездок про­водятся на ЭВМ расчеты распределения энергии по­ездов средневзвешенной массы по подстанциям. При этом достаточно провести расчеты для одной пары поездов, считая, что соотношения токов по плечам питания при другом количестве поездов из­меняются незначительно.

Решая систему уравнений (3.11), получаем, что зна­чения расходов активной и реактивной составляю­щих уравнительного тока в межподстанционной зоне Сохондо-Лесная.

W_ур(1-2)=W₁-( W₁+ W₂+ W₃)/(К+1),                        (3.12)

где ;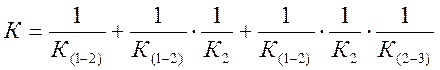

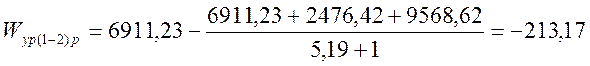 тыс. кВт·ч.,

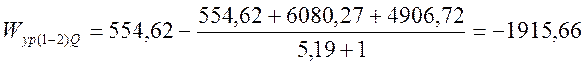 тыс. кВт·ч.

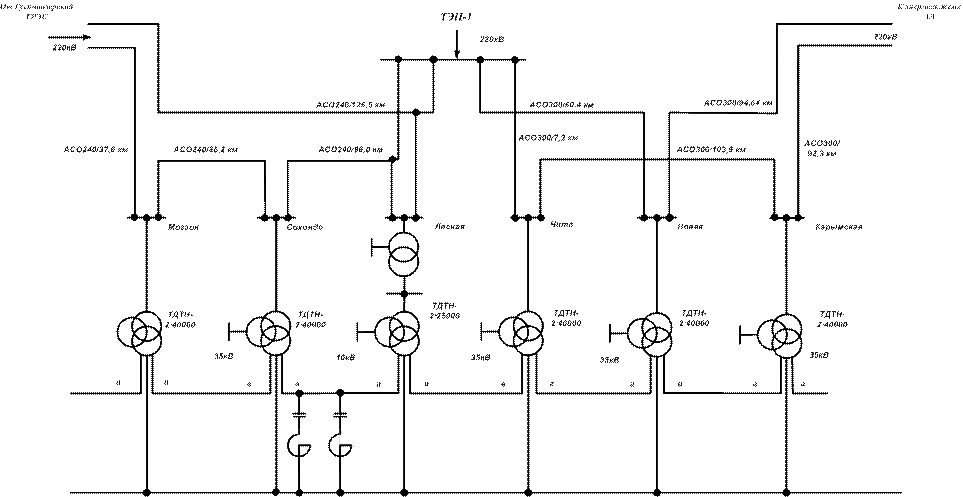
Рисунок 3.7-Схема внешнего электроснабжения расчетного участка

в межподстанционной зоне Лесная-Чита

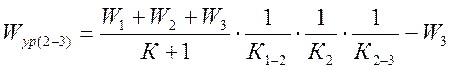                                        (3.13)

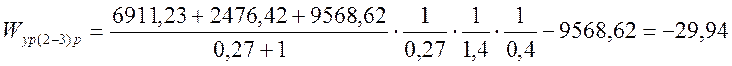 тыс.

кВт·ч.

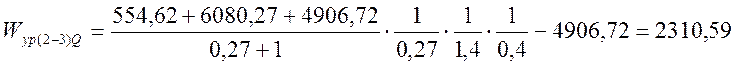 тыс.

кВт·ч.

По активной и реактивной  составляю­щим расхода уравнительного тока можно найти среднюю за период измерений величину уравнитель­ного тока:

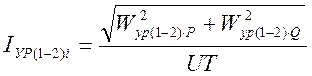,                                              (3.14)

где U — среднее за время измерений напряжение в контактной сети;

       Т — время, за которое определя­лись расходы W₁ ,W₂ ,W_3.

Cредняя за период измерений величина уравнитель­ного тока для МПЗ Сохондо-Лесная.

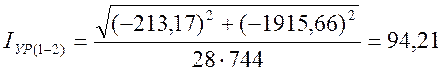 А.

Средняя за период измерений величина уравнитель­ного тока для МПЗ Лесная-Чит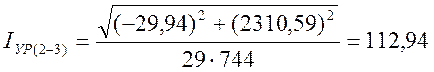а.

 А.

Потери в тяговой сети от уравнительного тока

ΔW_ур=I_ур²·R_ТС··Т,                                           (3.15)

где R_ТС  — активное сопротивление тяговой сети меж­подстанционной зоны . Для контактной подвески ПБСМ 95+МФ 100 R_ТС=0,138 Ом/км.

Потери в тяговой сети от уравнительного тока на участке Сохондо-Лесная за месяц.

ΔW_ур=744·94,21²·49,25·0,138·10^-6=57,28 тыс. кВт·ч.

Потери в тяговой сети от уравнительного тока на участке Лесная-Чита за месяц.

ΔW_ур=112,94²·64,15·744·0,138·10^-6=107,23 тыс. кВт·ч.

С целью проверки предложенной методики на участке Сохондо — Лесная — Чита Забайкальской  железной дороги были проведены экспе­риментальные исследования. Схема внешнего элек­троснабжения расчетного участка показана на рисунке 3.7.

Таблица 3.1 Результаты тяговых и электрических расчетов и расчетные значения уравнительного тока за январь 2001 года

Наименование подстанций	Длина	Расход э/э по 27.5 кВ		Расход акт. э/э  по мпз		Расход реакт. э/э по мпз		К	Расход от УТ, тыс. кВтч		уравнительный ток, А	Потери э/э от УТ	% от расходов
		актив- ный	реактив ный	слева	справа	слева	справа		актив-ный	реактив-ный		тыс. кВтч
Сохондо	49,2	6911,3	554,6	3282,84	3628,4	263,44	291,18
								5,19	-213,2	-1915,66	94,2	57,28	1,2
Лесная		2476,4	6080,2	953,42	1523	2340,9	3739,37
	64,1
Чита-1		9568,6	4906,7	5741,17	3827,45	2944,03	1962,69	0,27	-29,94	2310,59	112,9	107,23	1,4