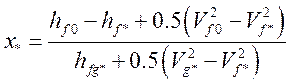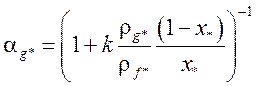Термогидравлический модуль РАТЕГ: модели, методы решения, страница 8

              ,

              .

3.2.7.2 Двухфазный теплоноситель

              В двухфазной области в основу модели критистечения положено условие критического течения, которое используется в кодах TRAC [ 14 ] и RELAP [ 15 ]:

              ,

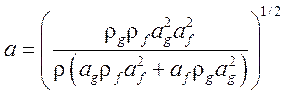               - скорость звука в теплоносителе [ 16 ],

а 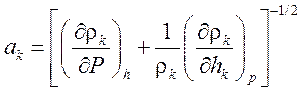 - скорости звука фаз.

              В моделях критического течения TRAC и RELAP в качестве второго уравнения для определения скоростей в критическом сечении используется разность уравнений скоростей фаз. Здесь второе уравнение: V_g* = k_*V_f*, где, коэффициент скольжения фаз в критическом сечении

k_* = min (k_crit_max, k),

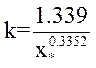[20],

k_crit_max = 3.

              Тогда

              .               (25)

              Давление теплоносителя в критическом сечении определяется из стационарного уравнения движения теплоносителя:

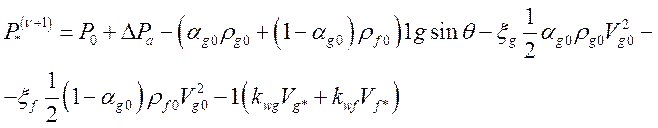,  (26)

,

.

              Термодинамические характеристики теплоносителя в критическом сечении определяются гак же, как в случае недогретой воды на входе. Паросодержание в критическом сечении определяется интегрированием стационарного уравнения сохранения энергии:

,

.

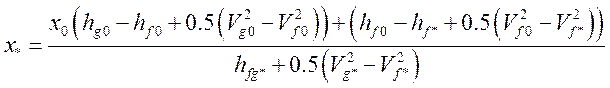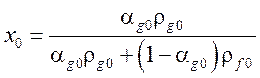              Далее

x_* = min (1, max, (x_*, x₀)),     (27)

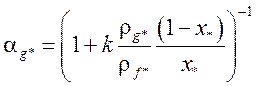              .                              (28)

              Из решения системы уравнений (26)-(28) вместе с уравнениями, определяющими энтальпии и плотности теплоносителя, а также скорость звука в критическом сечении  находится критический расход.

3.2.7.3 Парогазовый теплоноситель

              В случае парогазового теплоносителя параметры в критическом сечении вычисляются как для идеального газа [ 21 ]:

;

;

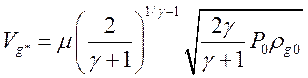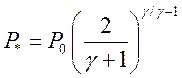              V_f* = V_g*;

              Γ = 1.3.

3.2.7.4 Промежуточные режимы

              В переходных режимах критическая скорость и давление в критическом сечении определяются интерполяцией по объемному паросодержанию между основными режимами. Например, критическая массовая скорость для режима 2:

.

3.2.7.5 Гидравлические коэффициенты истечения

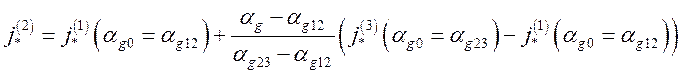              Гидравлические коэффициенты истечения определяются в соответствии с Таб. 2.1.

Таб. 2.1 Гидравлические коэффициенты истечения

Геометрия входа\режим	Недогретый,	Двухфазный,	Двухфазный,	Парогазовый,
Нет скачка сечения (Inlet=0)	1	1	1	1
Гладкая кромка (Inlet=1)	0.95	0.95	0.95	0.95
Острая кромка (Inlet=2)	0.9	0.9	0.9	0.9

3.2.8 Уравнения состояния и теплофизические свойства

3.2.8.1 Уравнения состояния фаз теплоносителя

              В РАТЕГ04 используются уравнения состояния воды и водяного пара в виде зависимостей:

;

;

;

;

.

              Кроме этих, основных, зависимостей из уравнений состояния определяются следующие, производные, необходимые для алгоритма расчета:

, , ,

.

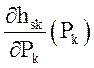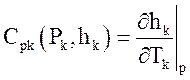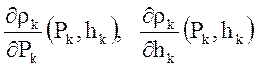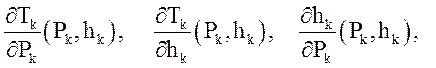
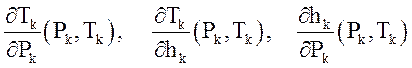              Уравнения состояния созданы на основе уравнений состояния кода TRAC [ 14 ].

3.2.8.2 Уравнения состояния неконденсируемых газов

              Предполагается, что неконденсируемые газы удовлетворяют уравнению состояния идеального газа. То есть,

, ,

, .

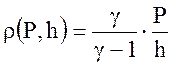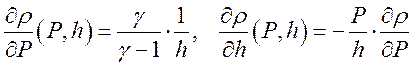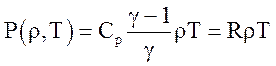              Параметры уравнений состояния для некоторых газов приведены в Таб. 2.2:

Таб. 2.2 Параметры уравнений состояния газов

3.2.8.3 Уравнение состояния смеси пара с неконденсирующимися газами

              При наличии в теплоносителе неконденсирующихся газов для определения необходимых величин и производных используется система:

,

,

,

,

,

.

3.2.8.4 Теплофизические свойства фаз теплоносителя и неконденсируемых газов

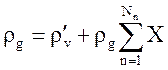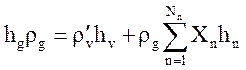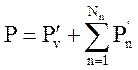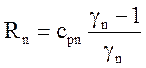              В РАТЕГ04 для определения замыкающих соотношений необходимы следующие теплофизические свойства:

-  динамическая вязкость в виде

-  коэффициент теплопроводности в виде

-  коэффициент поверхностного натяжения σ_fg(P).

              В настоящей версии кода используются доработанные соотношения кода ТРАС [ 14 ].

              Теплофизические свойства смеси пара с неконденсирующимися газами определяются следующими соотношениями [ 14 ]:

              , , .

3.3 Тепловые элементы

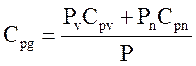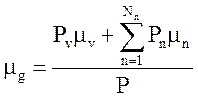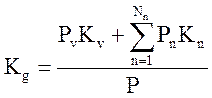              Под тепловым элементом (ТЭ) понимается твердый элемент конструкции, теплоперенос в котором и теплообмен которого с теплоносителем существенны для состояния ЯЭУ. Основные тепловые элементы: ТВЭЛы, стенки каналов, стенки парогенерирующих трубок парогенераторов и др. Тепловые элементы в РАТЕГ04 имеют осесимметричную геометрию и могут состоять из произвольного числа слоев из разных материалов. На Рис. 2.7 приведен пример гипотетического теплового элемента, который может моделироваться в РАТЕГ. Части с различной заливкой изображают различные материалы.

Рис. 2.7 Схема теплового элемента

              На торцевых границах ТЭ могут быть задана  температура или поток. На боковых границах могут быть заданы те же граничные условия, что и на торцевых, или тепловой элемент по этим границам может граничить с теплоносителем из одного или из разных каналов. Причем во внешнем канале скорость течения может быть направлена ортогонально к оси ТЭ (например, как для парогенерирующих трубок горизонтального парогенератора).

              Тепловые элементы могут быть простыми или кратными. Простой это одиночный ТЭ, а кратный – ТЭ, который представляет несколько полностью идентичных ТЭ.

3.3.1 Теплоперенос в тепловых элементах

              Перенос тепла в тепловых элементах рассчитывается в одномерном или двумерном осесимметричном приближении. В общем случае уравнение теплопроводности имеет следующий вид:

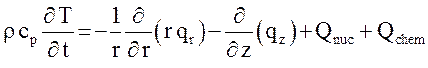,                    (29)

.

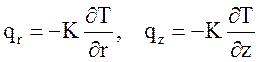              На границах могут быть заданы граничные условия 1-3 рода:

-  Температура,