Термогидравлический модуль РАТЕГ: модели, методы решения, страница 18

4.8.1 Проверка замкнутости контуров

              Блок проверки замкнутости контуров состоит из двух частей: блока нахождения замкнутых контуров в сети и блока проверки замкнутости найденных контуров.

              Блок нахождения замкнутых контуров работает по следующему алгоритму:

-  Нахождение замкнутых (по описанию) контуров начинается с первого элемента типа камера, если такого элемента нет, то с элементов типа  насос или замыкание.

-  Модуль, начиная с канала с наименьшим номером, выстраивает информацию о сети. При попадании в следующую камеру выстраивание продолжается по первому, не пройденному каналу, и так до попадания в исходную камеру.

              Например, для сети представленной на Рис. 3.5 первым будет определен контур: [1]—1—[2]—3—4—[3]—5—[4]—6—7—8—[1]. Здесь скобками обозначены камеры.

-  После этого алгебраическим  суммированием высот определяется, замкнут контур или нет.

-  Во всех камерах метятся пройденные каналы.

-  Процедура повторяется, начиная с предпоследней пройденной камеры.

              В нашем случае при этом будет обнаружен замкнутый контур: [3]—5—[4]—9—10—[5]—11—[3].

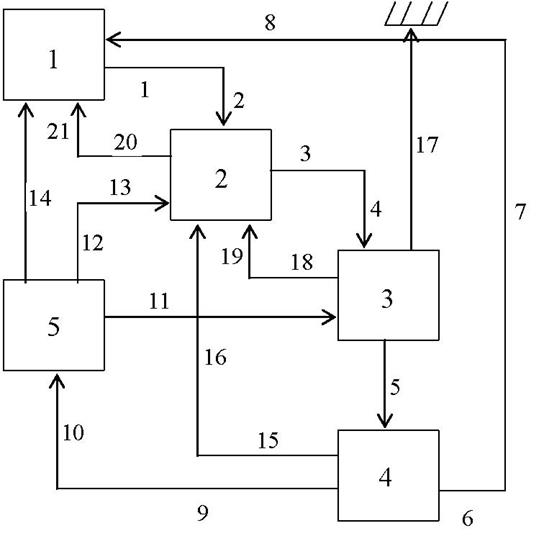
Рис. 3.5 Пример структуры сети

              Далее, действуя по аналогии, будут обнаружены контуры:

3. [2]—3—4—[3]—5—[4]— 9—10—[5]—12—13—[2];

4. [1]—1—2—[2]—3—4—[3]—5—[4]— 9—10—[5]—14—[1];

5. [2]—3—4—[3]—5—[4]— 15—16—[2];

6. [2]—3—4—[3]—18—19—[2];

7. [1]—1—2—[2]—20—21—[1].

              Остальные контуры проверять не нужно, так как их замкнутость следует из свойства транзитивности. Например, если контуры 5 и 6 замкнуты, то замкнут и контур [2]—19—18—[3]—5—[4]—15—16—[2].

              После нахождения всех замкнутых (по описанию) контуров проверяется их действительная замкнутость по условию:

,

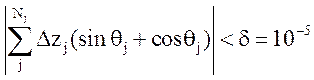ПРИЛОЖЕНИЕ А. Разностные формулы

              Уравнение неразрывности газовой фазы:

.

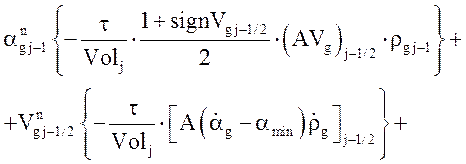
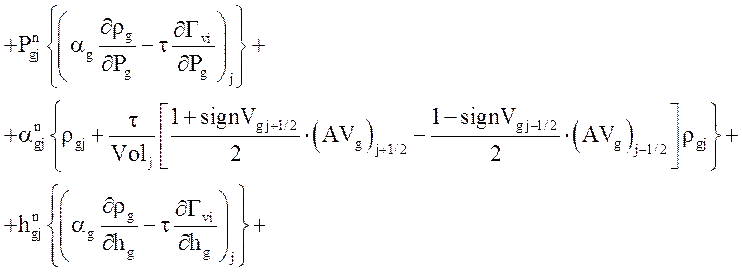
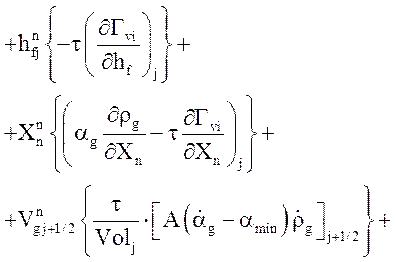
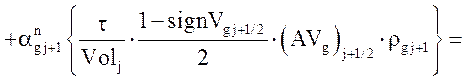
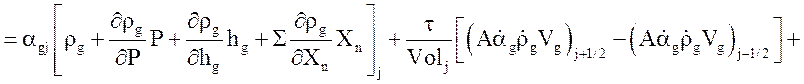
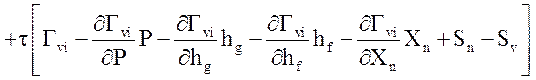              Уравнение неразрывности жидкой фазы:

.

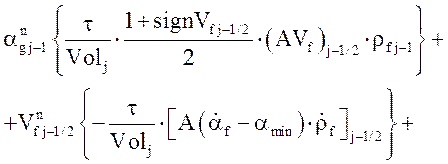
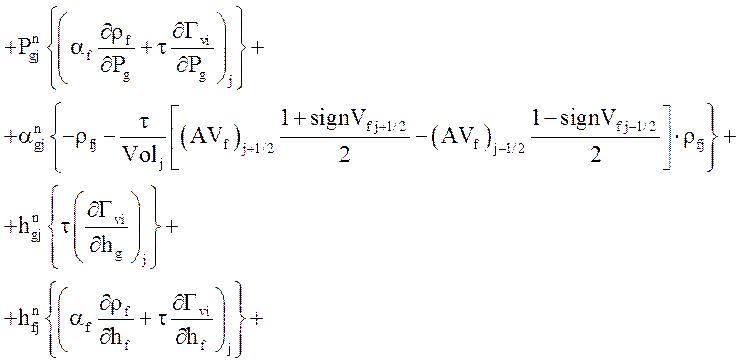
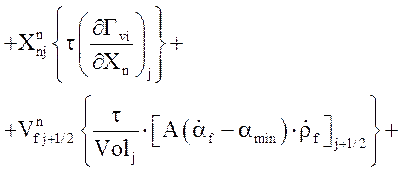
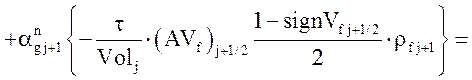
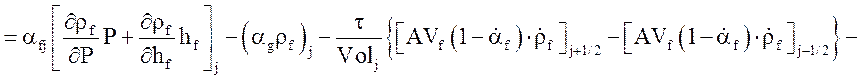
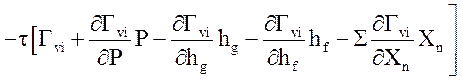              Уравнение энергии газовой фазы:

.

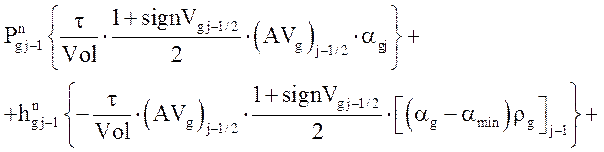
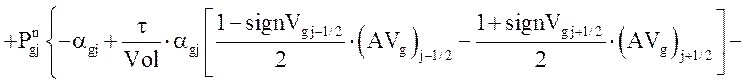
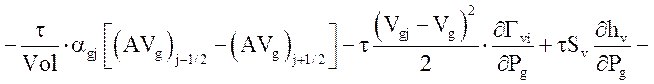
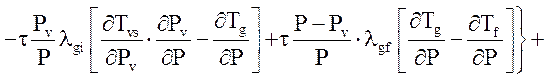
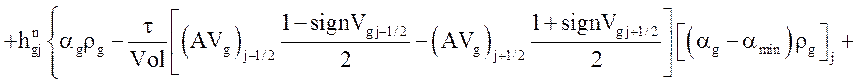
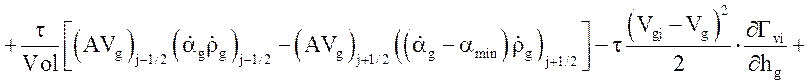
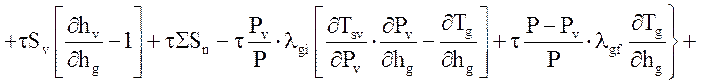
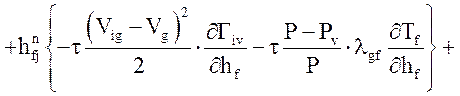
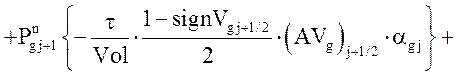
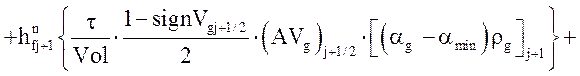
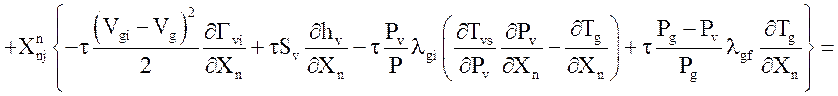
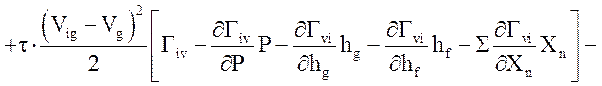
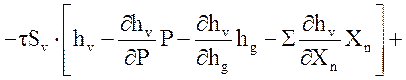
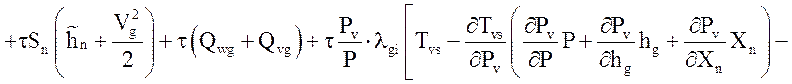
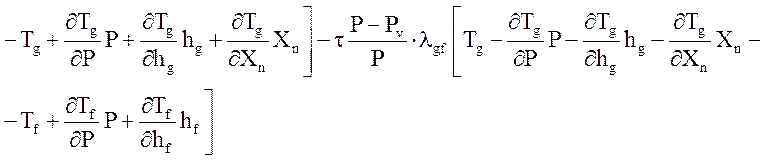              Уравнение энергии жидкой фазы:

.

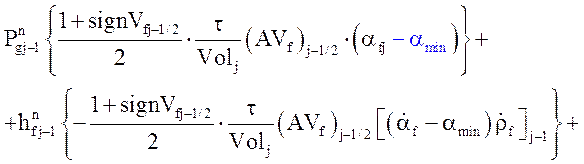
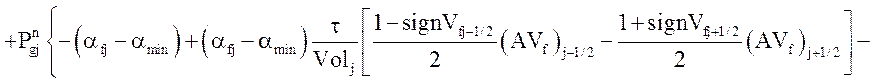
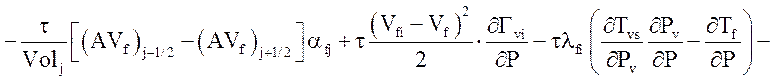
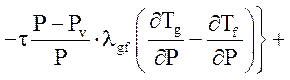
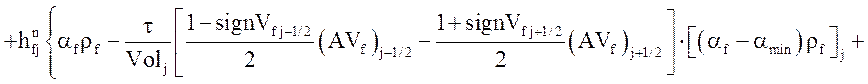
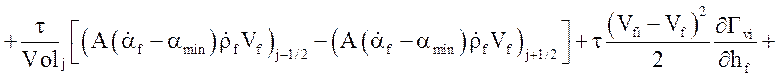
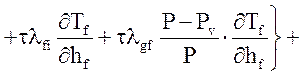
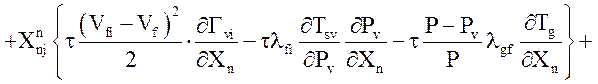
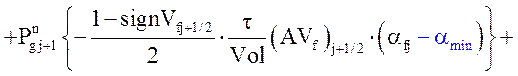
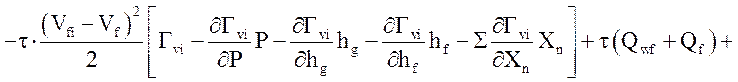
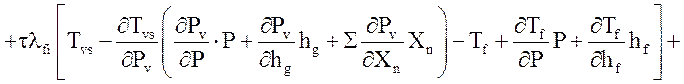
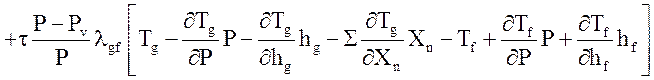              Уравнение движения газовой фазы:

.

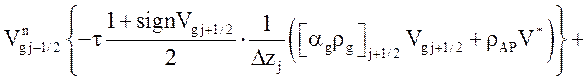
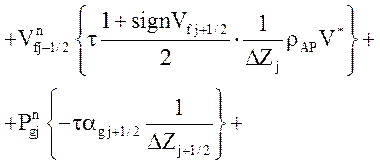
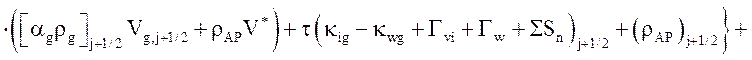
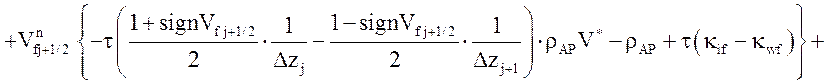
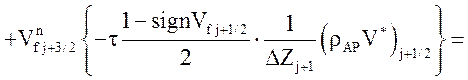
              Уравнение импульса жидкой фазы

.

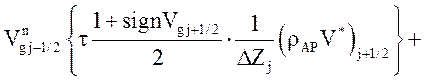
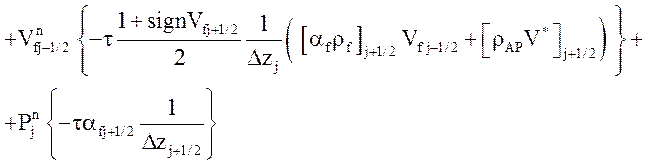
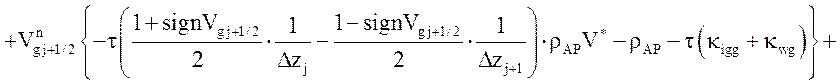
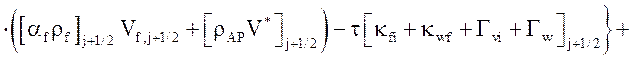
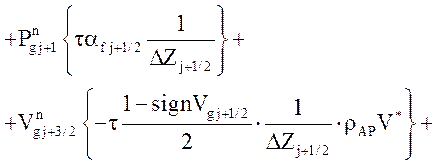
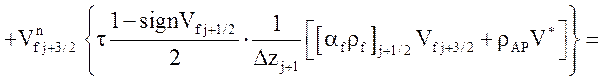
              Уравнение неразрывности неконденсирующегося газа:

.

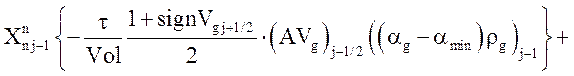
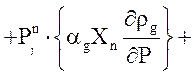
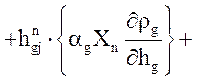
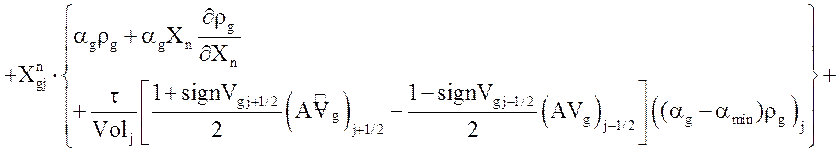
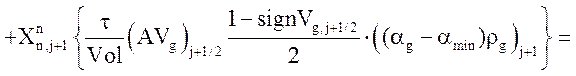
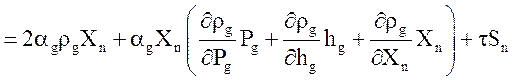ПРИЛОЖЕНИЕ Б. Алгоритм расчета состояния в критическом сечении

              Входные данные блока расчета состояния в критическом сечении:

-  геометрические параметры канала: l, μ_f(1), μ_f(2), μ_g(2), μ_g(1), А или d;

-  параметры теплоносителя во входном объеме: P₀, α_g0, ρ_g0, h_g0, V_g0, ρ_f0, h_f0, V_f0;

-  давление на выходе: Р₁.

              Выходные данные: j_*, P_*, k.

Если P₀ < P₁ выход (нет критистечения).

              Определение режима

              Режим 1. (недогретый теплоноситель)

если T_f0 < (T_s)P₁ и l > 0.01 на 1

иначе (невскипающий теплоноситель или диафрагма)

,

,

,

α_k* = α_k0, ρ_k* = ρ_k0, h_k* = h_k0

выход

1. (вскипающий теплоноситель)

,

,

,

.

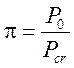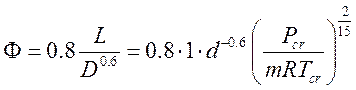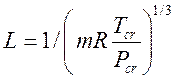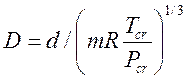(Метод Ньютона)

              (Выбор начального приближения)

ν = 0,

θ₀ = 5*10^-4 ( Первый заход. В последующих - θ₀ определено.),

,

,

,                                (ПБ.1)

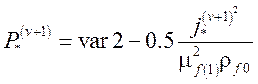,                      (ПБ.2)

,                                     (ПБ.3)

flag = 0.

2. Если T_s = 273.15

Если flag = 2 выход

var3 = θ₀,

θ₀ = 2θ₀,

уравнение (ПБ.1),

уравнение (ПБ.2),

уравнение (ПБ.3),

flag = 1,

на 2

иначе если ,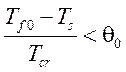

если flag = 1 выход

var3 = θ₀,

θ₀ = 0.5θ₀,

уравнение (ПБ.1),

уравнение (ПБ.2),

уравнение (ПБ.3),

flag = 2,

на 2

иначе

flag = 3

конец если

Если flag = 2

var4 = θ₀,

θ₀ = var3,

var3 = var4

конец если

Если flag не равен 3

3.

var4 = θ₀,

θ₀ = 0.5(var3+θ₀),

уравнение (ПБ.1),

уравнение (ПБ.2),

уравнение (ПБ.3),

Если T_s = 273.15

var3 = θ₀,

θ₀ = var4,

на 3

Конец если

если 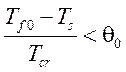 на 3

конец если

θ₀ - начальное приближение для итераций Ньютона.

4.

v > 100 сообщение, выход

уравнение (ПБ.1),

уравнение (ПБ.2),

уравнение (ПБ.3),

,

,

,

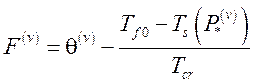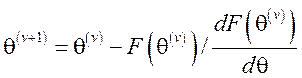v = v + 1

если  на 4

k = 1

выход.

Режим 3. (двухфазный теплоноситель)

ρ₀ = α_g0ρ_g0 + (1 - α_g0)ρ_f0,

,

,

,

,

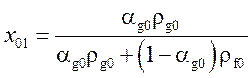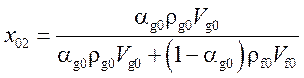 - начальные значения для метода половинного деления.

v = 0

1. v = v + 1,

v > 100 сообщение, выход

,

,

,

,

,

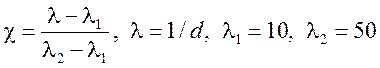μ = 0,

.

2. μ = μ +1,

μ > 100 сообщение, выход

,

,

,

,

,

,

,

,

,

,

,

,

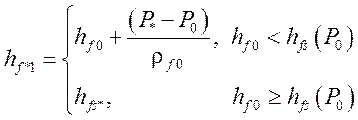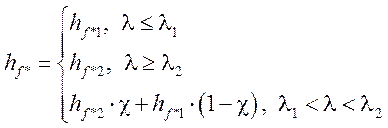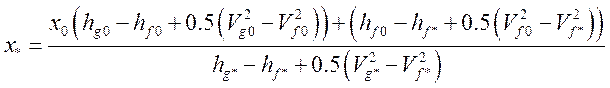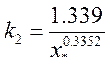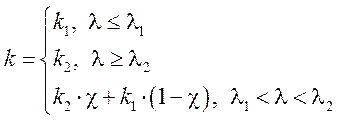если  на 2

,

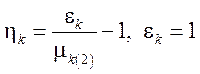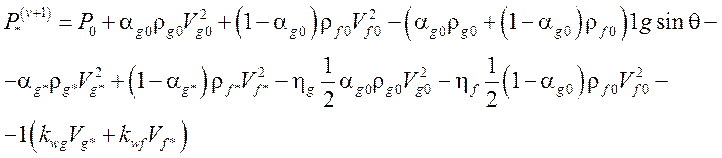
если  выход с сообщением

если 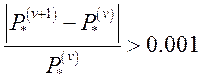 на 1

выход.

Режим 5. (Парогазовый теплоноситель)

,

,

,

,

,

,

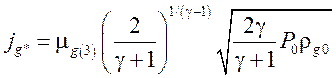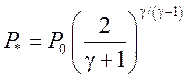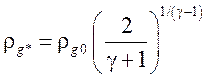k = 1

выход.

Режим 2.

,

,

,

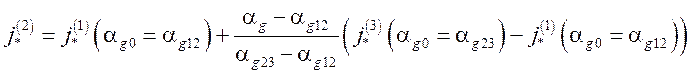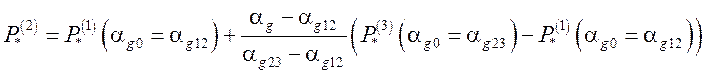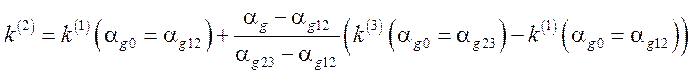выход.

Режим 4.

,

,

,

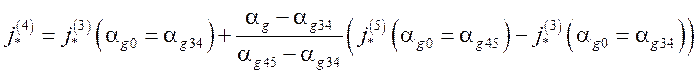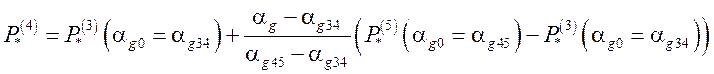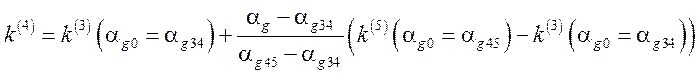выход

ПРИЛОЖЕНИЕ В. Соотношения для межфазного теплообмена[1]

Пузырьковый режим:

;

T_g > T_sv           ,

;

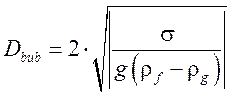T_g ≤ T_sv ;

T_f > T_s   ;

T_f ≤ T_s             ,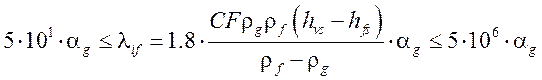

,

,

.

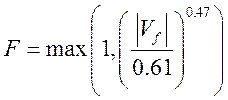Кольцевой и расслоенный режимы:

100 ≤ λ_gf = 4·10⁶α_f.

α_f ≥ 0.005,

T_g > T_sv           ,

T_g ≤ T_sv ;

T_f > T_s   ;

T_f ≤ T_s             ,

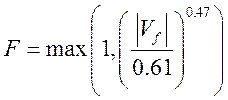
α_f < 0.005:

T_g > T_sv           ,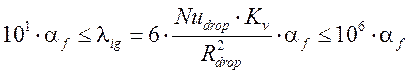

              ,

                        ,

                                    .

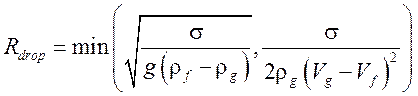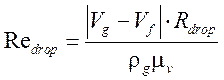T_f ≤ T_s   ,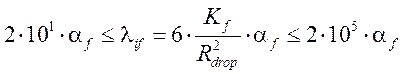

              ,

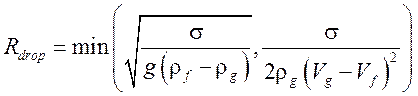СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

[ 1 ] Воронова О.А., Гатилова Р.Я., Ивченко Т.Г., Самигулин М.С. Программа РАТЕГ для численного моделирования нестационарной термогидравлики ядерных реакторов. // 4я Ежегодная Научно-Техническая Конференция Ядерного Общества:"Ядерная энергия и безопасность человека". Нижний Новгород. 28.06-2.07, 1993. Рефераты конференции. ч.2, 719-721.

[ 2 ] Воронова О.А., Гатилова Р.Я., Ивченко Т.Г., Самигулин М.С. Программа РАТЕГ для численного моделирования нестационарной термогидравлики сетей с двухфазным теплоносителем. Математическая модель и метод численного решения. // Вопросы атомной науки и техники. Сер. Математическое моделирование физических процессов. 1994, вып. 4.

[ 3 ] Самигулин М.С., Воронова О.А., Данилов Ю.Ф., Крутько Н.А., Шкарубский И.И. Системный двухжидкостной термогидравлический код РАТЕГ. Моделирование термогидравлики ВВЭР-1000 на внутрикорпусной стадии тяжелой аварии. В сборнике: Вопросы безопасности АЭС с ВВЭР. Том 2. Анализ аварийных ситуаций: компьютерные коды и экспериментальные исследования. Труды научно-практического семинара. С Петербург, 12-14 сентября 2000г, 13-25.