Термогидравлический модуль РАТЕГ: модели, методы решения, страница 16

o  если

§  

o  иначе

§  .

4.5.3.2.3 Блок определения плотностей, давлений и энтальпий компонентов газовой фазы

              Алгоритм определения  следующий:

-  , ;

-  μ = 0;

-  определяется ;

-  М1: µ = µ + 1;

-  , ;

-  если

o  , ,

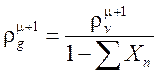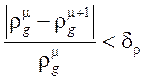o  если ( или ),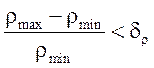

§  , ,

§  , ,

§  , ,

§  уход (итерации сошлись)

o  иначе

§  если , то ,

§  иначе ,

§  ,

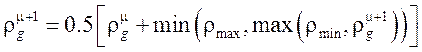o  идти на М1

-  иначе

o  ,

o  ,

o  идти на М1.

4.5.3.2.4 Блок определение интервала, в котором лежит решение

              На первой итерации интервал не известен: k_min = k_max = 0.

              Определение верхней границы интервала:  

              Если k_max = 0 и , то .

              Если k_max = 1 и , то .

              Определение нижней границы интервала:

              Если k_min = 0 и , то .

              Если k_min = 1 и , то .

4.5.4 Расчет теплопереноса излучением

              Система уравнений для определения эффективных потоков излучения на поверхности излучающих тепловых элементов имеет следующий вид:

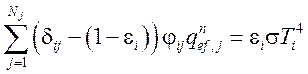.                            (36)

              Из этой системы по температурам с нижнего временного слоя определяются новые значения эффективных потоков тепла. В этой версии программы предполагается что, коэффициенты черноты и видимости постоянны. Поэтому матрица системы  (36) обращается на стадии подготовки расчета. По известным эффективным потокам определяются результирующие потоки излучения для каждого ТЭ:

.

4.5.5 Решение уравнений теплопроводности

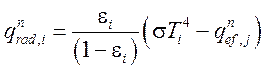              Системы линейных разностных уравнений теплопроводности, как для радиального направления, так и для продольного могут быть представлены в виде:

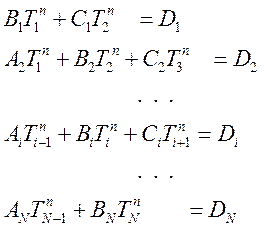
              Решается такая система методом прогонки [ 27 ]:

              На прямом ходе определяются прогоночные коэффициенты

,

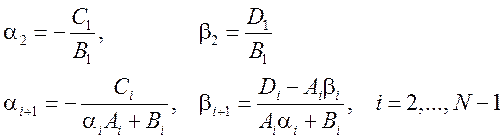а на обратном ходе получается решение:

.

4.6  Методы решения систем линейных уравнений

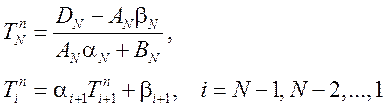              Библиотека решателей систем линейных уравнений РАТЕГ04 Newt (на FORTRAN 77) содержит решатели, основанные как на прямых, так и итерационных методах. Более подробно библиотека решателей описана в [ 28 ].

4.7  Критерии точности и выбор временного шага

              В ходе решения контролируется выполнение ряда критериев, определяющих точность учета различных процессов:

-  точность сохранения массы теплоносителя и неконденсирующихся газов;

-  изменение за временной шаг: массы фазы в ячейке за счет массообмена, массы неконденсирующихся газов, давления, энтальпий фаз, температуры стенки;

-  выход параметров теплоносителя за допустимые пределы: .

              Далее, в зависимости от критериев и от степени отклонения решения от критериев производятся:

-  определение величины временного шага на следующий шаг;

-  изменение величины временного шага и пересчет шага.

              Все условия ограничения и пересчета шага сведены в Таб. 3.1. Более подробно эти условия описаны ниже.

Таб. 3.1 Условия ограничения и пересчета шага

Номер	Условие или номер раздела с подробным описанием	Условие ограничения шага	Условие пересчета	Опция включения/выключения ограничения или пересчета
0		Максимально допустимый шаг (τ ≤ τmax)	-	-
1	3.7.2	Условие сохранения массы	γ > MC_MAX	MassConservation 1/0
3		Изменение температуры стенки за шаг	ΔT > WTV_MAX	WallTempVariation 1/0
2		Число итераций при вычислении температуры газа	-	IterationNumber 1/0
4		Скорость изменения табличной функции	-	TableVariation 1/0
5		Критическое истечение	При Vk > Vs без изменения шага	RecountToChokedFlow 1/0
6			Выход параметров теплоносителя за допустимый интервал	RecountToInadmissibleParam 1/0
7		Точный выход на время окончания расчета	-	ExactFinish 1/0
8	-		Не сошлись итерации при решении системы линейных уравнений	-
9		Ограничение энерговыделения в газовую фазу	-	-
10		Ограничение межфазного теплообмена	-	RecountToMassTransfer 1/0
11			Межфазный массообмен	-
13			Изменение параметра за шаг больше допустимого	-

4.7.1 Ограничение шага условиями сохранения массы

              Использование неконсервативных разностных схем для аппроксимации законов сохранения позволяет, с одной стороны, получить простую легко разрешимую систему разностных уравнений, с другой, вынуждает ограничивать временной шаг условием точности сохранения массы. Для выбора шага, удовлетворяющего этому условию, в программе используется алгоритм, аналогичный алгоритму из [ 4 ]. Суть алгоритма в следующем. После расчета шага по линеаризованным уравнениям определяется погрешность, вносимая в закон сохранения массы, и новый временной шаг определяется из условия ограничения этой погрешности. Если погрешность на шаге превышает определенное значение, то производится пересчет шага с уменьшением величины счетного шага. Рассмотрим этот алгоритм подробнее.

              Консервативное решение, удовлетворяющее закону сохранения, получается из уравнения

.

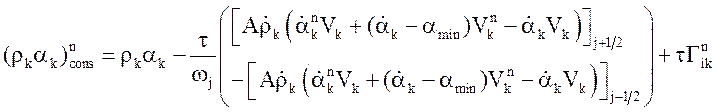              Линеаризованное решение получается из уравнения

.

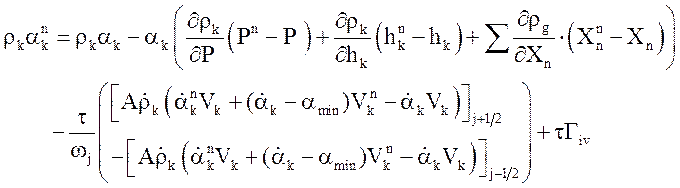              Вычитая из первого уравнения – второе (для исключения старой приведенной плотности) получим, что для сохранения массы новая плотность должна удовлетворять уравнению

,

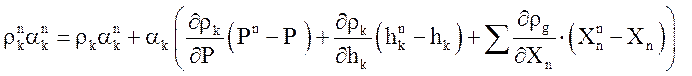но она определяется из уравнения состояния

,

что вносит в закон сохранения абсолютную погрешность

.

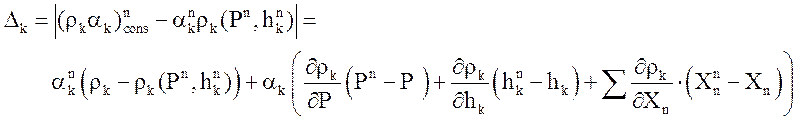              Чтобы ограничить погрешность в сохранении массы, определяется максимальная относительная погрешность