Модель истечения недогретого вскипающего теплоносителя используется, если Tf0 – Ts(P1 > 0), то есть θ > 0. Зависимость массовой скорости от θ показана на Рис. 3.3. Минимальное θ и максимальный расход получается при P* = P1. Определим из этого условия начальное приближение, в предположении отсутствия трения о стенку:
![]() ;
;
![]() .
.
Если П01 ≤ 0 то критическое течение отсутствует.
3.2.5.3.1..2 Двухфазный теплоноситель
В двухфазной области используется метод половинного деления. Алгоритм решения описан в приложении.
Уравнения теплопроводности аппроксимируются на прямоугольной пространственной сетке (Рис. 3.1). Сетка вдоль оси элемента совпадает с пространственной сеткой соответствующего гидравлического канала. Температура определена на границах ячеек сетки, а плотность и теплофизические величины − в ячейках сетки.
В РАТЕГ04 для учета теплопроводности используется осесимметричное приближение, одномерное или двумерное. В двумерном случае система разностных уравнений решается расщеплением по направлениям.
Для аппроксимации по времени используем схему с весами (σ = 1/2). Пространственная аппроксимация получаются интегрированием по объему окружающему точку определения температуры (на Рис. 3.1 заштрихован).
Для радиального направления:
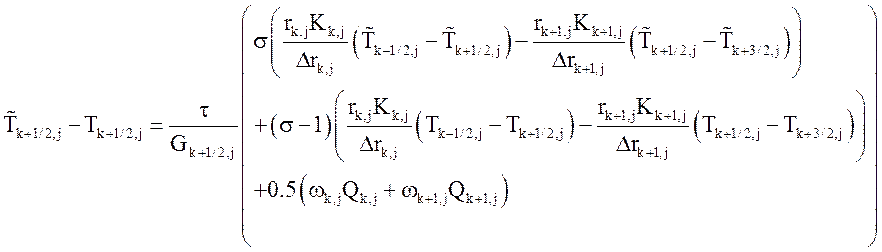 .
.
Для продольного направления:
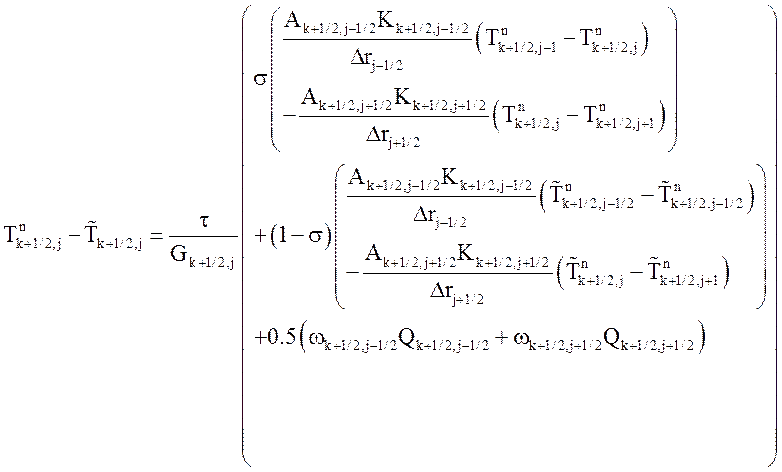 .
.
Здесь:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
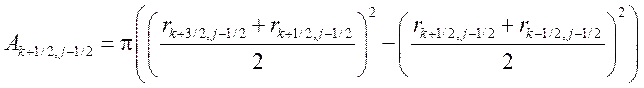 ;
;
![]() .
.
Если на границах заданы потоки, разностные уравнения для граничных интервалов имеют вид:
- На боковых границах:
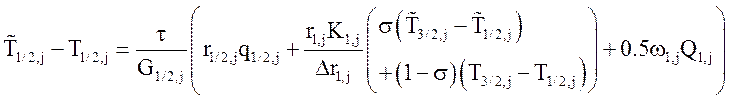 ;
;
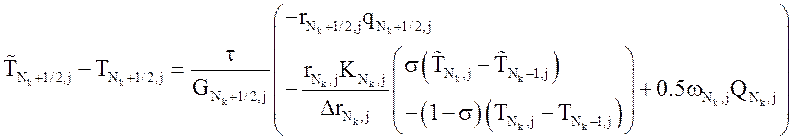 .
.
- На торцовых границах:
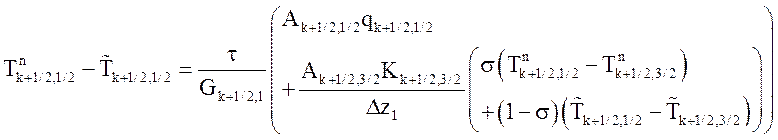 ;
;
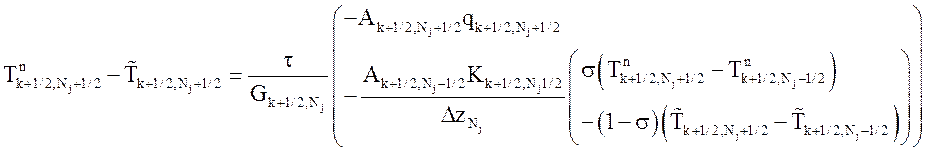 .
.
В РАТЕГ04 реализованы две модели центробежных насосов (см. раздел 2.4.4).
Система уравнений, описывающая работу насоса модели 1, аппроксимируется следующей системой разностных уравнений:
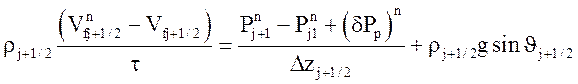 ,
,
![]() ,
,
или
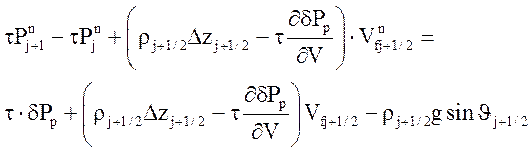 .
.
Перепад давления создаваемый насосом на верхнем временном слое определяется соотношением:
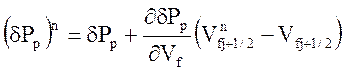 ,
,
где перепад давления на нижнем слое и производная
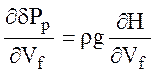 (35)
(35)
определяются в зависимости от используемых зависимостей для напора (см. таблица 2.1).
Перепад давления:
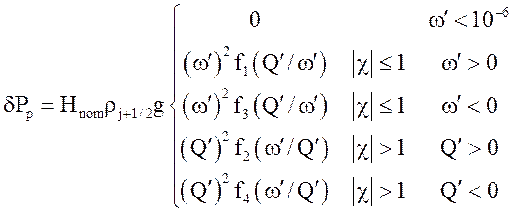 .
.
Здесь 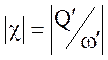 .
.
Определим производную:
при ![]()
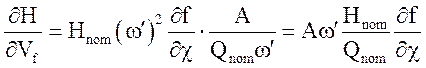 ,
,
при ![]()
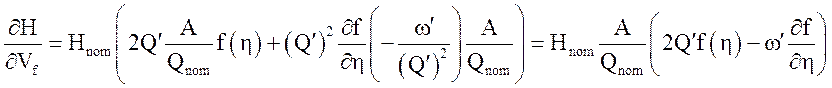 ,
,
где ![]() .
.
Тогда производная от перепада давления по скорости определяется следующими соотношениями:
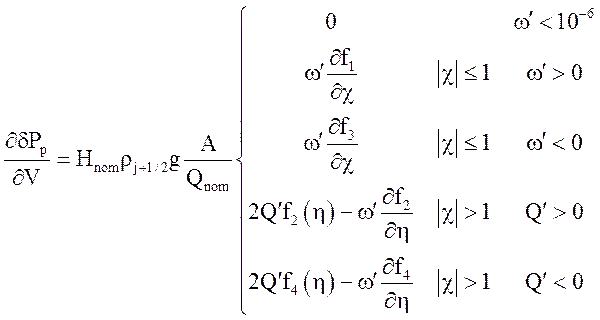 .
.
Уравнение, описывающее изменение угловой скорости вращения вала насоса при выбеге, аппроксимируется уравнением:
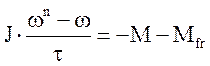 .
.
Далее
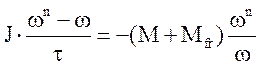 ,
, 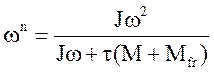 .
.
Гидравлический момент сопротивления определяется по характеристикам насоса
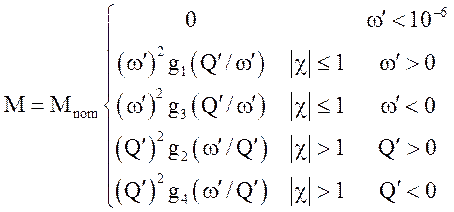 .
.
Модель 2 на разностной сетке насос моделируется одним узлом сетки, в котором уравнения движения заменяются следующими:
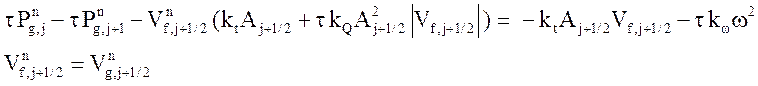 .
.
Давление в емкости на верхнем слое находится из уравнения
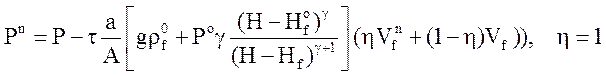 ,
,
которое аппроксимирует дифференциальное уравнение:
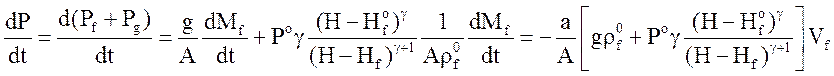 .
.
Здесь
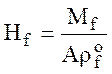 .
.
Скорость на входе в трубопровод определяется как для отвода из камеры:
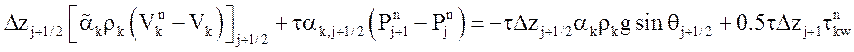 .
.
Далее рассчитывается новая масса воды в емкости:
![]() .
.
Полная система уравнений, описывающих поведение ЯЭУ, решается в следующей последовательности:
- По системе уравнений термогидравлики рассчитывается новое состояние теплоносителя в системе. При этом тепловые потоки стенка-теплоноситель берутся с нижнего временного слоя.
- По уравнениям теплопереноса излучением определяются эффективные тепловые потоки на поверхностях ТЭ. Температуры поверхности ТЭ берутся с нижнего временного слоя.
- Рассчитывается теплопроводность в ТЭ. Потоки ТЭ – теплоноситель берутся с нижнего временного слоя. Потоки за счет теплопереноса излучением определяются на предыдущем этапе.
- Вычисляются новые тепловые потоки ТЭ – теплоноситель.
- Рассчитываются новые концентрации жидкой примеси.
В общем случае система разностных уравнений
содержит (6 + Nn)N линейных уравнений (и столько же
неизвестных ![]() ). Для неразветвленного участка сети
это система линейных уравнений вида:
). Для неразветвленного участка сети
это система линейных уравнений вида:
![]() ,
,
где ![]() , а A,B,C-матрицы с размерностью (6 + Nn)х(6 + Nn). В
развернутом виде система имеет следующий вид:
, а A,B,C-матрицы с размерностью (6 + Nn)х(6 + Nn). В
развернутом виде система имеет следующий вид:
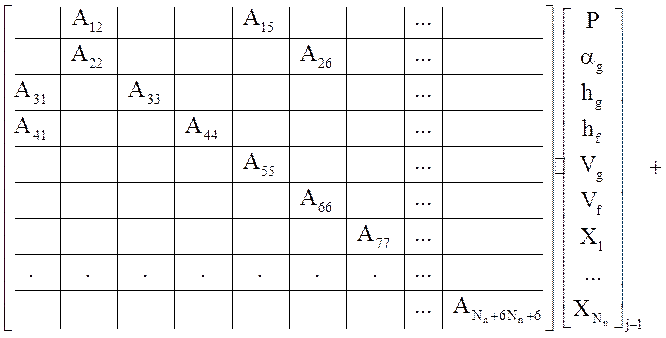
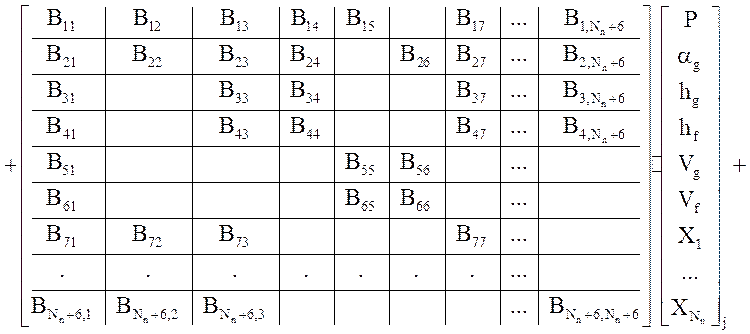
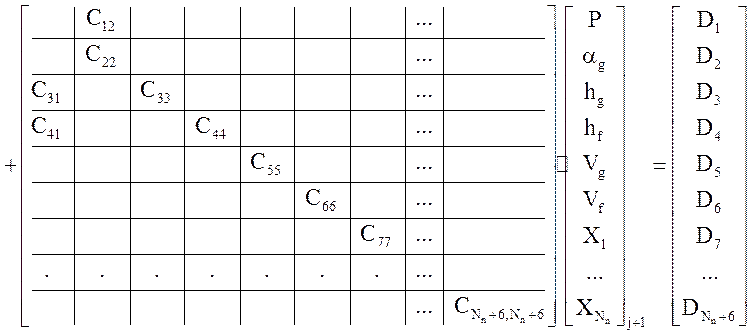 .
.
Система решается с помощью модулей решения систем линейных уравнений [ 28 ].
При наличии неконденсируемых газов для определения ρg, Tg их производных, а также параметров пара и неконденсирующихся газов через независимые переменные P, hg и Xn используется система:
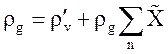 ,
,
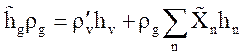 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Это система 5+2Nn нелинейных
уравнений с 5+2Nn неизвестными: ![]() .
.
При отсутствии пара система имеет аналитическое решение:
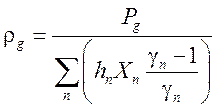 ,
,
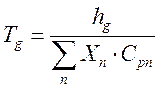 ,
,
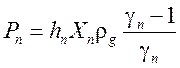 ,
,
![]() .
.
В общем случае система решается итерационным методом, общая схема которого описана ниже:
- kmin = kmax = 0;
- ν = 0;
-
![]() ;
;
- M1: ν = ν + 1;
-
блок вычисления ![]() от
от
![]()
-
блок вычисления ![]()
-
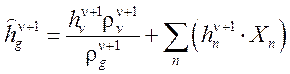 ;
;
-
если 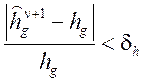 уход;
уход;
- блок определения интервала решения;
- идти на М1.
Опишем подробнее отдельные блоки алгоритма решения.
Алгоритм вычисления температуры газовой фазы следующий:
-
если ν = 0 ![]() (заданное начальное
приближение);
(заданное начальное
приближение);
- иначе
решается система линейных
уравнений, из которой определяется вектор неизвестных: ![]()
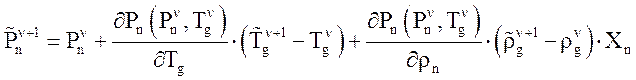 ,
,
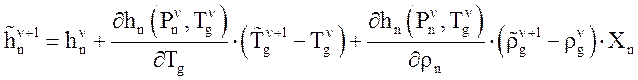 ,
,
![]() ,
,
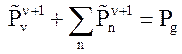 ,
,
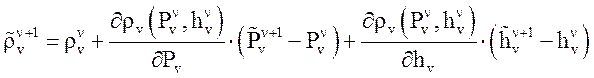 ,
,
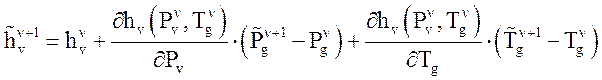 ,
,
![]() .
.
Далее проводится корректировка температуры газа:
- если (kmin = 1 и kmax = 1)
o
если ![]()
§
![]()
o иначе
§
![]() ;
;
- если (kmin = 1 и kmax = 0);
o
если ![]()
§
![]()
o иначе
§
![]() ;
;
- если (kmin = 0 и kmax = 1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.