Термогидравлический модуль РАТЕГ: модели, методы решения, страница 14

              В общем случае:

              ,

              ,

       .

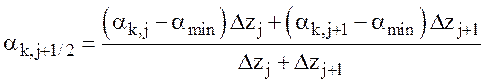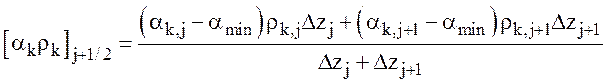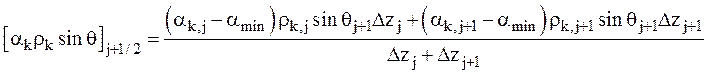              Для узлов граничащих с ячейками, в которых возможна вертикальная стратификация:

              ,

              ,

,

              .

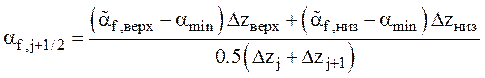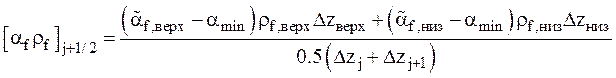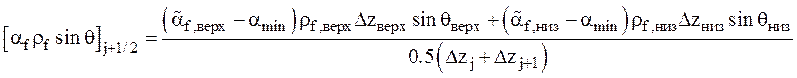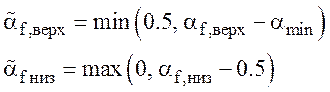              Значения других скалярных величин в узлах сетки определяется:

.

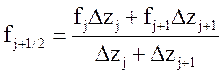              Гидростатическое давление в горизонтальных каналах:

              ,

              .

4.2.2.3  Аппроксимация в камерах

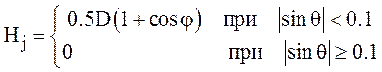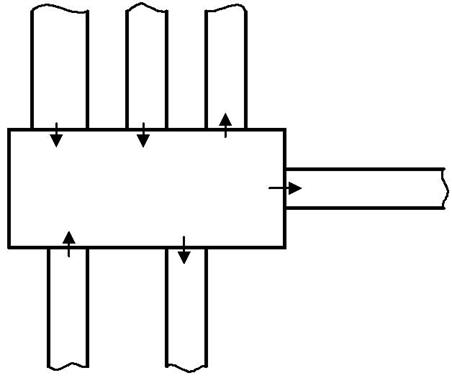
Рис. 3.2 Схема камеры

              Аппроксимация уравнений в камерах (Рис. 3.2) несколько отличается от аппроксимации в неразветвленных участках сети. В уравнениях неразрывности и сохранения энергии меняется аппроксимация операторов дивергенции вида Ñ(Vf). После интегрирования уравнений по объему камеры с учетом теоремы Гаусса- Остроградского получим следующую аппроксимацию операторов дивергенции: 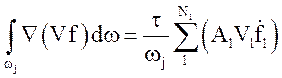. Здесь суммирование по каналам связанным с камерой, знак скорости положительный для потока из камеры, величины на входе/выходе каналов определяются «донорным» способом.

              Аппроксимация уравнений движения на срезе каналов, присоединенных к камере (на Рис. 3.2 помечены стрелками) отличается аппроксимацией переносного члена (в случае, когда течение из камеры) и члена, описывающего трение о стенки.

              Трение о стенки учитывается только в канале и не учитывается в камере. Аппроксимация переносного члена зависит от характера течения в канале. Выделяются отводы (близки по назначению элементу tee branch кода RELAP [ 15 ]) и каналы основного течения (соответствуют one-dimensional branch кода RELAP). Элемент RELAP crossflow branch может быть воспроизведен соединением камер каналом нулевой длины.

              При аппроксимации переносного члена в отводах предполагается, что скорость в направлении отвода в центре камеры равна нулю. Отсюда аппроксимация уравнения скорости на срезе отвода (течения из камеры, нумерация сетки от камеры):

.

              Для каналов основного течения (течения из камеры, нумерация сетки от камеры):

.

              Скорости на верхнем и нижнем слое в камере определяются усреднением:

,

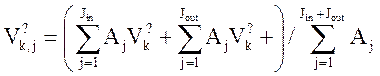где суммирование по входящим в камеру и выходящим из камеры каналам, а верхний индекс ? определяет нижний или верхний временной слой.

4.2.3 Аппроксимация обменных членов

4.2.3.1  Межфазное трение

.

              Применено сглаживание межфазного трения

.

4.2.3.2  Межфазный массообмен

              Межфазный массообмен на верхнем слое определяется как:

.

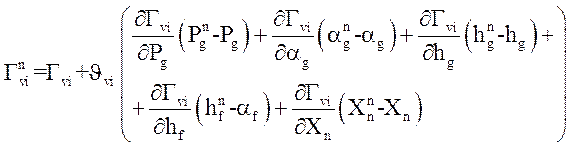              По умолчанию . Может меняться опцией: TETA_VI=

              В разностных уравнениях используется скорректированное значение , которое определяется как:

,

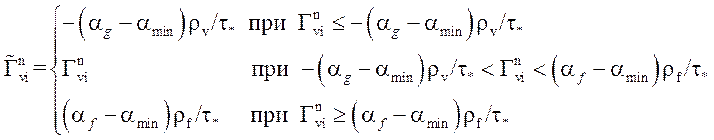τ_*=min(τ, 0.001).

              В первом и третьем случае производные от интенсивности массообмена полагаются равными нулю.

4.2.3.3  Теплообмен стенка-теплоноситель

              Общая схема расчета теплообмена стенка-теплоноситель существенно ограничивает временной шаг при конвекции в парогазовую смесь. Это связано с колебаниям теплового потока, вызванными малой теплоемкостью парогазовой смеси при высоких температурах и независимостью потоков от разных тепловых элементов друг от друга. Для устранения этого недостатка при расчете теплообмена конвекцией в газовую фазу используется «квазинеявная» аппроксимация температуры теплоносителя.

              Расчет теплового потока организован в три этапа:

-  определяется поток с нижнего слоя;

-  прогнозируется (предвычисляется) новая температура теплоносителя;

-  корректируется поток с учетом предвычисленной  температуры теплоносителя.

              Предвычисленная температура газовой фазы определяется с учетом только потоков тепла:

.

              Отсюда

.

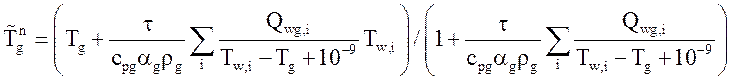              Далее корректируются потоки

.

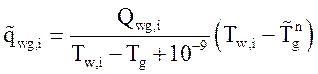              Теперь они зависят друг от друга через предвычисленную температуру теплоносителя.

              В дальнейшем эту схему предполагается распространить на другие режимы теплообмена.

4.2.4 Аппроксимация уравнения переноса примеси

              Перенос жидкой примеси рассчитывается после решения основных уравнений. Разностное уравнение для определения новой концентрации примеси в каналах:

.

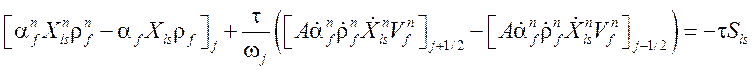              Аппроксимация переносного члена в камерах аналогична аппроксимации этого члена в уравнениях неразрывности и энергии фаз теплоносителя.

4.2.5 Аппроксимация моделей критического течения

4.2.5.1  Модель 1

              Модель реализована следующим образом. В конце каждого временного шага в заданных сечениях системы проверяется выполнение условия , если оно не выполняется, то шаг пересчитывается с заменой уравнения движения на условие: .

4.2.5.2  Модель 2

              Если выполняется условие

  ,

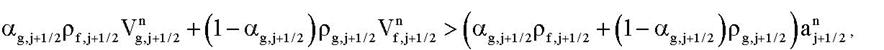 то шаг пересчитывается  с заменой уравнений движения на: 

  

 

4.2.5.3 Модель 3

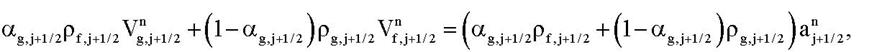
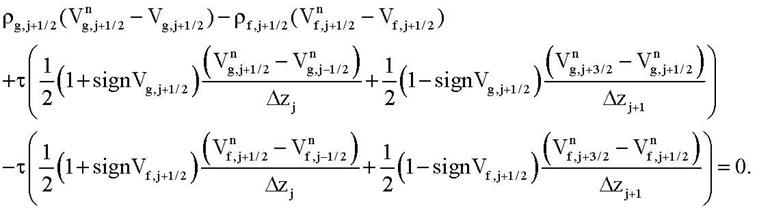
              Критическое течение возникает в, так называемом, критическом «сечении». В данной модели критическое «сечение» может представлять весь канал (конечной или нулевой длины), часть канала или сечение канала (с нулевой длиной).

              На расчетной сетке КС представляется узлом, в котором специальным образом определяется скорость.

              В случае если в КС возможно критическое течение, на каждом временном шаге (после расчета основных величин) происходит обращение в блок критического течения, в котором определяется критическая массовая скорость и давление в критическом сечении.

              Если j > j_* и P_* > P₁ и P₀ > P₁ временной шаг пересчитывается со следующим определением скоростей фаз в КС:

,

.

              Усреднение с весами сделано для уменьшения (исключения) осцилляций. В этой версии δ = 0.1.

              После линеаризации получаем:

,

,

.

4.2.5.3.1 Определение критического расхода и состояния в критическом сечении

4.2.5.3.1.1 Недогретый теплоноситель

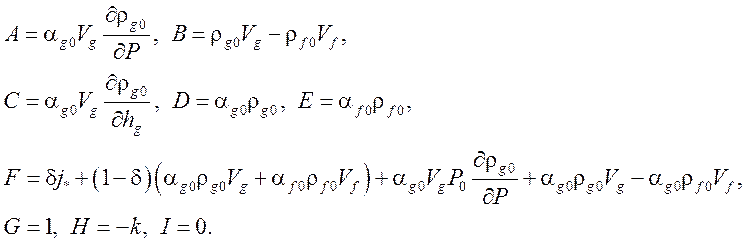              В недогретой области используется метод Ньютона. Система уравнений (22)-(24):

,

,

,

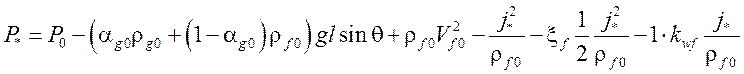представляются в виде:

,

,

.

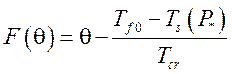Тогда

,

.

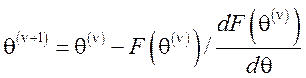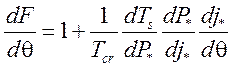              Определение начального приближения.

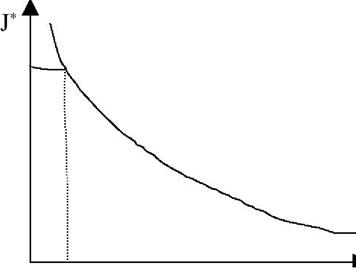
Рис. 3.3 Зависимость массовой скорости от θ

Начальное приближение.