Термогидравлический модуль РАТЕГ: модели, методы решения, страница 7

              При турбулентной конденсации теплообмен описывается соотношением для турбулентной конвекции для воды (16).

              Тепловой поток за счет конденсации передается на межфазную границу:

              , q_wf = 0, q_wg = 0.

3.2.5.3.9 Промежуточные режимы

              Для промежуточных режимов используется линейная интерполяция.

-  Промежуточные режимы 26, 36, 46, 56

              Алгоритм определения потоков в этом случае:

              if α_g < α_g1

                        q_wg = q_wg,NB-FB, q_wf = q_wf,NB-FB, q_wi = q_wi,NB-FB,

              if α_g > α_g2

                        q_wg = q_wg,FCG, q_wf = q_wf,FCG, q_wi = q_wi,FCG,

              if α_g1 ≤ α_g≤ α_g2

                        q_wg = χq_wg,NB-FB + (1-χ)q_wg,FCG

                        q_wf = χq_wf,NB-FB + (1-χ)q_wf,FCG

                        q_wi = χq_wi,NB-FB + (1-χ)q_wi,FCG

             

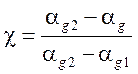
                        α_g1 = 0.92

                        α_g2 = 0.96.

              Здесь индекс NB-FB обозначает одно из соотношений из «цепочки» соотношений: пузырьковое кипения (в недогретом состоянии или в состоянии насыщения в зависимости от температуры) - переходное кипение – пленочное кипение.

-  Промежуточные режимы 17

              При T_w < T_sv

              if α_g < α_g1

                        q_wg = q_wg,FC, q_wf = q_wf,FC, q_wi = q_wi,FC,

              if α_g > α_g2

                        q_wg = q_wg,C, q_wf = q_wf,C, q_wi = q_wi,C,

              if α_g1 ≤ α_g≤ α_g2

                        q_wg = χq_wg,FC + (1-χ)q_wg,C

                        q_wf = χq_wf,FC + (1-χ)q_wf,C

                        q_wi = χq_wi,FC + (1-χ)q_wi,C

             

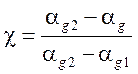
                        α_g1 = 0.04

                        α_g2 = 0.06.

3.2.6 Гидростатическое давление в горизонтальном канале

              Учет гидростатического давления в горизонтальных каналах необходим для описания процесса растекания жидкости в горизонтальных каналах при стратификации. Гидростатическое давление в канале:

              P_hg = 0, P_hf = H_ρfg,

              .

3.2.7 Критическое течение

              В РАТЕГ04 реализованы три модели критического течения.

              Модель 1. Скорость фаз теплоносителя ограничивается скоростью звука в теплоносителе:

              V_k = min(V_k, a),                                    (20)

где 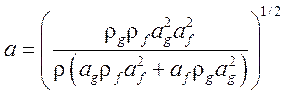 - скорость звука в теплоносителе [ 16 ],

а 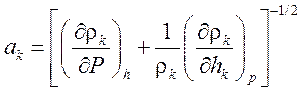 - скорости звука фаз.

              Модель 2 представляет собой упрощенную версия модели [ 15 ] для двухфазных течений. В конце каждого временного шага в заданных сечениях системы проверяется выполнение условия:

              ,

если оно выполняется, то шаг пересчитывается с заменой уравнении движения на:

              ,

              .

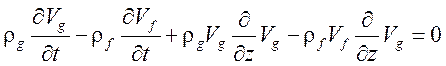              Второе уравнение получено вычитанием из уравнения скорости газа, умноженного на концентрацию воды, уравнения скорости для воды, умноженного на концентрацию пара и отбрасыванием обменных членов.

              Модель 3. В настоящее время отсутствуют достаточно точные универсальные, пригодные для всех состояний теплоносителя, модели критического течения. Поэтому, в модели 3 в зависимости от состояния теплоносителя на входе в канал, где возможно запирание потока используются разные модели критического течения. Выделены следующие режимы:

Жидкий (недогретый) теплоноситель	Переходный	Двухфазный теплоноситель	Переходный	Парогазовый теплоноситель
1	2	3	4	5
αg12 = 0.001               αg23 = 0.1                   αg34 = 0.99                  αg45 = 0.9999

3.2.7.1 Недогретый теплоноситель

              В зависимости от температуры недогретый теплоноситель может вскипать при истечении или оставаться в недогретом состоянии. Для этих случаев используются разные модели. Для невскипающего теплоносителя (T_f0 ≤ T_s (P₁)) массовая скорость определяется из уравнения Бернулли по давлениям на концах канала:

              ;

              V_f* = j_*/ρ_f0;

              V_g* = V_f*.

              В основу модели для недогретого вскипающего теплоносителя  положена модель Авдеева-Лабунцова [ 24 ] для истечения через цилиндрические трубы из больших объемов, которая получена на основе анализа размерности и обобщения экспериментальных данных.

              В этой модели давление и скорость в критическом сечении находятся из следующей системы уравнений:

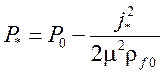              ,                                    (21)

              ,                         (22)

              ,                                  (23)

где: 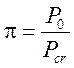, , 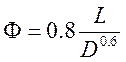, , 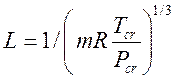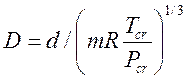а m – масса кг-моля (для воды 18).

              В РАТЕГ эта модель используется  и для истечения в случаях, когда должна быть учтена скорость вверх по потоку, гравитационная составляющая перепада давления и трение о стенки канала, то есть вместо уравнения (21) используется уравнение:

  ,

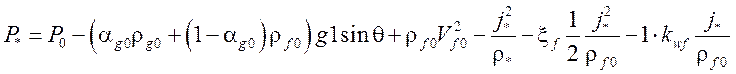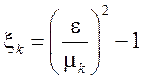 - коэффициент сопротивления входа,

ε - коэффициент сжатия (в данной версии кода ε = 1),

μ_k - коэффициент истечения.

              Пользователь имеет возможность задать или коэффициент сопротивления входа или коэффициент истечения.

              Для упрощения решения полагается ρ_* = ρ_f0.

              Тогда

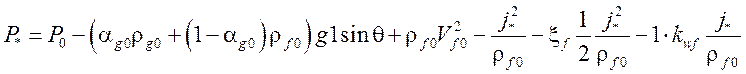.   (24)

              Из решения системы уравнений (22)-(24) определяется критический расход. После определения критического расхода скорости фаз находятся из стационарных уравнений неразрывности:

              V_f* = j_*/(α_g*ρ_g*k + (1 - α_g*) ρ_f*),

              V_g* = kV_f*.

              Термодинамические характеристики теплоносителя определяются на основе следующих предположений:

-  пар в критическом сечении находится в состоянии насыщения

              h_g* = h_vs (P_*), ρ_g* = ρ_g (P_*, h_g*)

-  энтальпия воды в критическом сечении:

              ,

              ,

              h_f*2 = h_fs*,

              ,

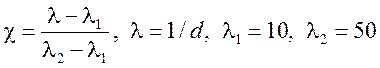              ρ_f* = ρ_f (P_*, h_f*).

              Паросодержание в критическом сечении определяется интегрированием стационарного уравнения сохранения энергии: