В общем случае канал представляет собой усеченный конус с разными основаниями. Каналы более сложной формы могут быть набраны из элементарных каналов. В каналах некругового сечения термогидравлический диаметр определяется формулой Dh = 4A/П. Канал может граничить с произвольным числом тепловых элементов, с которыми происходит теплообмен.
Возможны каналы нулевой длины. Они используются для моделирования перетечек между объемами разделенными диафрагмами, перфорированными перегородками и др.
Элемент камера используется для моделирования объемов, которые связаны с более чем двумя каналами. В общем случае камера может быть соединена с каналами соединениями трех типов: прямоток, отвод, перетечка.
Прямоточные каналы это каналы лежащие в направлении основного потока теплоносителя. Они при подготовке входного файла снабжаются специальным признаком. Такое соединение вместе с элементом камера позволяют создавать модели различных разветвлений, коллекторов, в том числе элементы типа one-dimensional branch кода RELAP5/MOD3.2
Соединение канала и камеры типа «отвод» предназначено для моделирования тройников, врезок труб в трубы большего диаметра и др. Соединение типа отвод аналогично элементу tee branch кода RELAP5/MOD3.2.
Соединение типа «перетечка» это соединение двух камер каналом нулевой длины. Такое соединение по аналогии с элементом crossflow branch кода RELAP5/MOD3.2 позволяет моделировать межканальные перетечки
Камера характеризуется объемом и гидравлическим диаметром направления основного потока. Расстояния от центральных сечений камеры до срезов каналов определяются при описании соответствующих каналов.
В камере могут быть заданы источники:
- неконденсирующихся газов;
- жидкой примеси;
- тепловыделения в теплоносителе;
- теплоносителя (инжекторы).
Камера может граничить с тепловыми элементами.
Граничные условия могут моделировать:
- разрывы и предусмотренные связи с внешней средой, например, через предохранительные клапаны;
- элементы реально не учитываемые в расчетной модели: питательные и др. насосы, емкости, и др.
Подробнее возможные граничные условия описаны в РУКОВОДСТВЕ ПОЛЬЗОВАТЕЛЯ.
В РАТЕГ04 реализованы две модели центробежных насосов. Первая модель используется, если известны четырехквадрантные характеристики насоса, вторая – если известны зависимости напора от расхода.
В первой модели работа центробежного насоса описывается следующей системой уравнений, аналогичной [ 14 ]:
Vg = Vf = V;
.
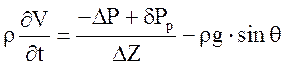
Напор, как правило, выдается в виде
зависимостей от объемного расхода и угловой скорости вращения вала насоса. В
данной модели угловая скорость вращения либо задается в виде таблиц 
, либо определяется по уравнению
(только в режиме выбега) 
.
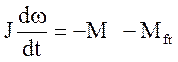В общем (двухфазном) случае напор и момент
сопротивления представляются в следующем виде: 
,
.
Здесь величины с индексом 1ф определяются по характеристикам для однофазной среды, а величины с индексом 2ф – по характеристикам для двухфазной среды при паросодержании дающем наименьший напор. Коэффициенты К задаются в виде зависимости от паросодержания, для однофазных случаев они равны 0.
Напор Hкф и момент сопротивления Mкф
определяются по так называемым четырехквадрантным характеристикам насоса,
выдаются изготовителем насоса. Эти характеристики представляют собой
зависимости напора и момента сопротивления от 
и
, при разных режимах работы насоса. В
Таб. 2.3 определены условия выбора зависимостей для определения напора и
момента сопротивления. 
полагается, что: 
.
Таб. 2.3 Выбор зависимостей для напора и момента сопротивления
|
|
|
||
|
Вид зависимости |
|||
|
|
|
||
|
ω > 0 |
ω < 0 |
Q > 0 |
Q < 0 |
|
f1, g1 |
f3, g3 |
f2, g2 |
f4, g4 |
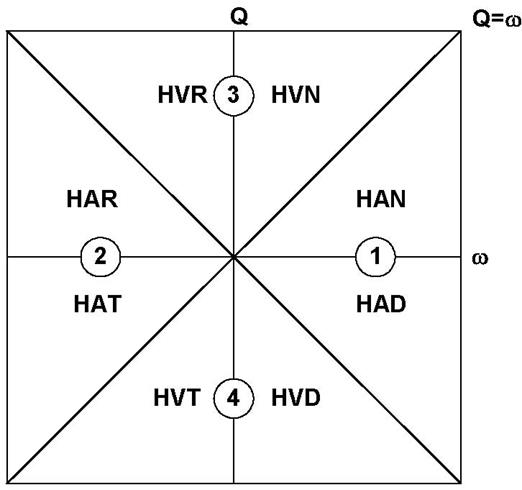
Рис. 2.9 Соответствие таблиц РАТЕГ и RELAP. Таблицы РАТЕГ обозначены цифрами
В РАТЕГ, в отличие от RELAP, смежные по расходу или по угловой скорости таблицы объединены в одну таблицу (см. Рис. 2.9), поэтому задаются по 4 таблицы для напора и момента сопротивления, а не 8 как в RELAP.
Момент сопротивления трения в подшипниках и
уплотнителях задается в виде кусочно-линейной табличной зависимости 
. Значения момента для промежуточных
угловых скоростей определяется интерполяцией: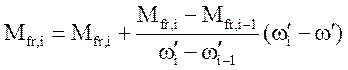 
.
Модель 2 центробежного насоса используется в
случае, когда не известны четырехквадрантные характеристики. Предполагается,
что изменение расхода через насос происходит за счет скачка давления,
создаваемого насосом, силы трения, которая пропорциональна квадрату расхода, и
силы воздействия крыльчатки насоса на теплоноситель, которая пропорциональна
квадрату угловой скорости вращения, то есть: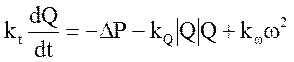 
.
Коэффициенты уравнения зависят от свойств насоса и теплоносителя и могут быть определены по гидравлическим (стационарным и динамическим) характеристикам насоса.
Элемент емкость используется для моделирования емкостей открытых в атмосферу и гидроаккумуляторов. Модель реализована в виде граничного условия на входе в трубу, соединяющую емкость с системой (см. Рис. 2.10). Давление на входе в трубу равно сумме гидростатического давления и давления на поверхности воды P = Pg + Pf.
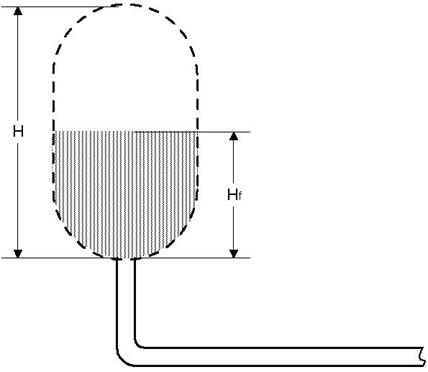
Рис. 2.10 Схема емкости
Гидростатическое давление: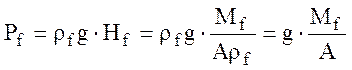 
.
Давления на поверхности воды может быть заданным, если это открытая емкость Pg = Pa или определяться давлением в газе, если это гидроаккумулятор. Давление в газе определяется из предположения адиабатического расширения газа:
.
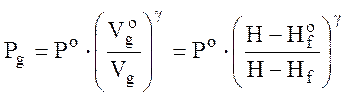
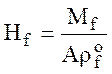Для сосудов открытых в атмосферу 
.
Масса воды в емкости определяется уравнением: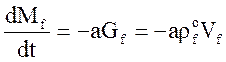 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
