Факультет Автоматики и Вычислительной Техники
Кафедра ССОД

Курсовая работа
По дисциплине «Теория и обработка сигналов»
«Проектирование цифрового полосового БИХ-фильтра Баттерворта»
Вариант 6
Выполнил: Преподаватель:
студент гр. АТ-43 доцент Щетинин Ю.И.
Шавлак Е.В.
2007
Содержание
Введение 3
Техническое задание 4
Обоснование выбора и сущность метода проектирования 5
Проектирование фильтра 7
Реализация фильтра 14
Тестирование фильтра 19
Программирование фильтра и оценка быстродействия 24
Заключение 27
Список литературы 28
Введение
Фильтром называется устройство (цепь), которое обеспечивает необходимую реакцию на какой-то входной сигнал. В основном, данная реакция заключается в выделении из входного сигнала, который представляет собой аддитивную смесь полезного сигнала с шумом, полезной составляющей, то есть определённые полезные свойства входного сигнала сохраняются в выходном сигнале, а нежелательные – подавляются.
Семейство фильтров весьма разнообразно, они классифицируются по разным параметрам.
Фильтры сигналов разделяются на аналоговые и цифровые. В аналоговых фильтрах производится преобразование аналоговых сигналов. Цифровой фильтр, работающий в реальном масштабе времени, оперирует с дискретными по времени данными в противоположность непрерывному сигналу, обрабатываемому аналоговым фильтром. При этом очередной отсчет, соответствующий отклику фильтра, формируется по окончании каждого периода дискретизации. Среди цифровых фильтров, в свою очередь, выделяют два фундаментальных класса: фильтры с конечной импульсной характеристикой (КИХ-фильтры) и фильтры с бесконечной импульсной характеристикой (БИХ-фильтры).
В зависимости от выделяемой полосы частот фильтры подразделяются на фильтры нижних частот (ФНЧ), верхних частот (ФВЧ), полосовые (ПФ) и режекторные (РФ, заграждающие).
Для аппроксимации характеристик фильтров используются специальные типы функций, которые могут быть реализованы в практических схемах. По названию аппроксимирующих функций соответствующие фильтры называю фильтрами Баттерворта, Чебышева, Бесселя, Кауэра и др.
Такое разнообразие цифровых фильтров призвано удовлетворять определенным потребностям в получении выходного сигнала.
Процесс проектирования цифровых фильтров состоит из тех же этапов, что и процесс проектирования аналоговых фильтров. Сначала формулируются требования к желаемым характеристикам фильтра, по которым затем рассчитываются параметры фильтра. Амплитудная и фазовая характеристики формируются аналогично аналоговым фильтрам. И в зависимости от требований, предъявляемых к выходному сигналу, получаются требования к самому цифровому фильтру. В итоге в каждом конкретном случае требуется спроектировать цифровой фильтр с теми или иными характеристиками [1].
В данной курсовой работе подробно рассмотрен синтез цифрового полосового БИХ-фильтра Баттерворта, в соответствии с техническим заданием.
Все расчеты по проектированию фильтра были выполнены в среде MatLab 6.5 фирмы The MathWorks, Inc.
Техническое задание
Разработайте цифровой полосовой БИХ - фильтр Баттерворта, удовлетворяющий следующим условиям:
§ Нижняя граничная частота полосы пропускания – 2 кГц,
§ Верхняя граничная частота полосы пропускания – 8 кГц
§ Нижняя граничная частота полосы задерживания– 1,2 кГц,
§ Верхняя граничная частота полосы задерживания – 11 кГц,
§ Минимальное ослабление в полосе задерживания – 40 дБ,
§ Допустимое ослабление в полосе пропускания – 3 дБ,
§ Частота дискретизации – 40 кГц.
Исходя из выше перечисленных требований, можно сделать соответствующие выводы о том, каким должен быть данный фильтр.
Во-первых, данный фильтр должен оперировать с дискретными по времени входными сигналами. Во-вторых, данный фильтр должен являться фильтром с бесконечной импульсной характеристикой. Для БИХ-фильтров характерна зависимость сигнала на выходе фильтра не только от значений входного сигнала, но и от значений выходного сигнала в предыдущие моменты времени. Необходимо, чтобы данный фильтр был устойчив, а для этого нужно, чтобы полюса спроектированного фильтра находились в пределах единичной окружности.
Полученный фильтр должен быть полосовым фильтром с нижней частотой среза равной 2000 Гц, верхней частотой среза равной 8000 Гц, нижней граничной частотой полосы задерживания равной 1200 Гц, верхней граничной частотой полосы задерживания равной 11000 Гц и с частотой дискретизации равной 40000 Гц. То есть данный фильтр должен почти без искажений пропускать частотные составляющие, лежащие в пределах от 2000 Гц до 8000 Гц входного сигнала, и почти не должен пропускать ту часть входного сигнала, которая лежит вне этих пределов. Слово “почти” означает, что данный фильтр, как и всякий другой реальный фильтр, будет, естественно, хуже своего идеального прототипа, то есть хуже идеального ФНЧ.
Фильтр, в данном случае, должен удовлетворять следующим требованиям, не упомянутым выше: ослабление в полосе задерживания должно быть не менее 40 дБ, а допустимая неравномерность коэффициента передачи в полосе пропускания составляет 3дБ.
Спроектированный фильтр должен удовлетворять спецификации, которая продемонстрирована на рис. 1.
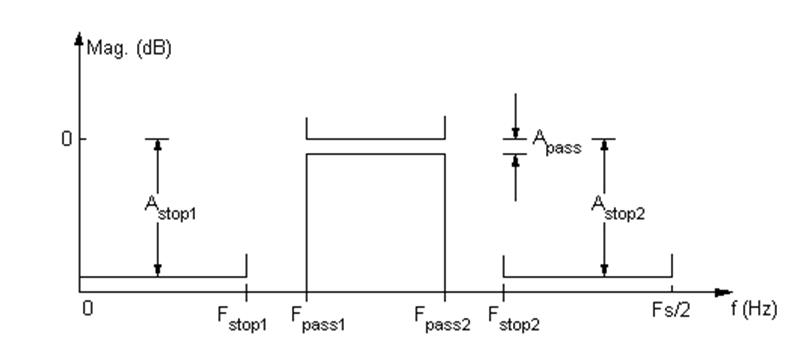
Рис. 1. График спецификации фильтра.
Обоснование выбора и сущность метода проектирования
Расчет БИХ-фильтра заключается в
определении значений коэффициентов ak,
bk для уравнения вида 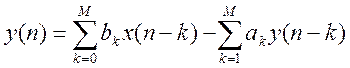 , обеспечивающих необходимый вид
амплитудной, фазовой или импульсной характеристик.
, обеспечивающих необходимый вид
амплитудной, фазовой или импульсной характеристик.
Наиболее широко при расчетах БИХ-фильтров используются методы, основанные на использовании аналоговых прототипов фильтров. Разработка и применение аналоговых прототипов исторически предшествовали цифровым фильтрам, их методы расчета хорошо развиты. Поэтому наиболее распространены методы расчета БИХ-фильтров, включающие проектирование соответствующего аналогового прототипа, и далее его передаточная функция преобразуется в плоскость z.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.