Разновидности преобразований и рядов Фурье (обзор)

Разновидности  преобразований и рядов Фурье (обзор)

Сигналы могут быть непрерывными и дискретными по времени, и также периодическими и апериодическими. Комбинации этих свойств дают следующие виды рядов и преобразований Фурье:

1.  Преобразование Фурье, ПФ  – частотное (спектральное) представление (разложение) непрерывного и апериодического сигнала. Его называют также непрерывно – временным преобразованием Фурье, НВПФ (англ. Continue Time Fourier Transform,  CTFT).
Выражение анализа     ,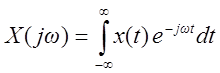

      выражение синтеза      .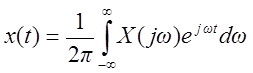
    Временная область:  x(t) – непрерывная и апериодическая функция t, 
    частотная область -  X(jω) – комплексная, непрерывная и  апериодическая функция  ω. 

2.  Ряд Фурье, РФ (англ. Fourier Series)
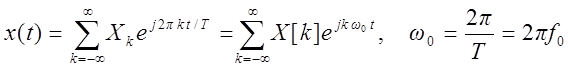 - выражение синтеза,
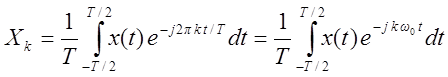 - выражение анализа,
x(t) – непрерывная и периодическая функция,
X_k – комплексная, дискретная и апериодическая функция k.

3.  Дискретно – временное преобразование Фурье, ДВПФ (англ. Discrete Time Fourier Transform, DTFT)
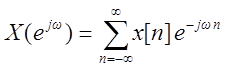 - выражение анализа,
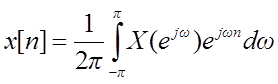 - выражение синтеза,
x[n] – дискретная и апериодическая функция n,

X(e^jω) – непрерывная и периодическая функция  ω с периодом от 0 до 2π.

4.  Дискретное преобразование Фурье,  ДПФ (англ. Discrete Fourier Transform, DFT).

  Это  преобразование называют также  дискретно – временным рядом Фурье

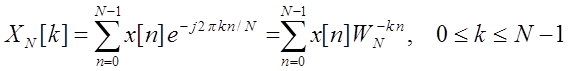, - выражение анализа,
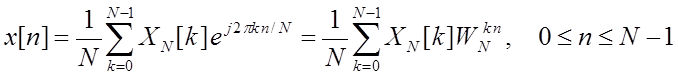- выражение синтеза.
x[n] – дискретная и периодическая функция n   с периодом   N,
X_N[k] – дискретная и периодическая функция k  с периодом N.