Министерство образования и науки Российской Федерации
Кафедра систем сбора и обработки данных
Курсовая работа
по дисциплине «Теория и обработка сигналов»
«Разработка цифрового БИХ - фильтра нижних частот Чебышева 2-го типа»
Факультет: АВТ Преподаватель:
Группа: АТ-53 доц. Щетинин Ю. И
Вариант: 9
Выполнила: Ездакова Е. Отметка о защите:
Новосибирск, 2008
Введение.. 3
1. Техническое задание.. 4
2. Обоснование выбора и сущность метода проектирования.. 5
3. Проектирование фильтра.. 7
3.1. Получение спецификации АФ на основе спецификации ЦФ.. 7
3.2. Проектирование аналогового прототипа. 8
3.3. Преобразование аналогового прототипа в цифровой фильтр. 8
4. Реализация фильтра.. 13
5. Тестирование фильтра.. 17
6. Программирование фильтра и оценка быстродействия.. 21
Заключение.. 24
Список литературы... 25
Цифровая обработка сигналов как направление развития науки и техники зародилась в 1950-х годах и поначалу представляла собой довольно экзотическую отрасль радиоэлектроники, практическая ценность которой была далеко не очевидной. Однако за прошедшие пятьдесят лет благодаря успехам микроэлектроники системы цифровой обработки сигналов не только воплотились в реальность, но и вошли в нашу повседневную жизнь в виде CD- и DVD-проигрывателей, модемов, сотовых телефонов и многого другого [3].
Из всех задач, решаемых при цифровой обработке сигналов, наиболее важной является задача фильтрации. Фильтром называется цепь (система, устройство), обеспечивающая необходимую реакцию на заданный входной сигнал. Основное применение фильтров заключается в выделении полезного сигнала из аддитивной смеси его с шумом. То есть фильтр преобразует входной сигнал таким образом, что определенные полезные гармоники входного сигнала сохраняются в выходном сигнале, а нежелательные подавляются.
Фильтры сигналов разделяются на аналоговые и цифровые. В аналоговых фильтрах производится преобразование аналоговых (непрерывных) сигналов. Цифровой фильтр, работающий в реальном масштабе времени, оперирует с дискретными по времени данными. При этом очередной отсчет, соответствующий отклику фильтра, формируется по окончании каждого периода дискретизации. Среди цифровых фильтров, в свою очередь, выделяют два фундаментальных класса: фильтры с конечной импульсной характеристикой (КИХ-фильтры или нерекурсивные) и фильтры с бесконечной импульсной характеристикой (БИХ-фильтры или рекурсивные) [1].
В зависимости от полосы частот прохождения сигнала фильтры подразделяются фильтры нижних частот (ФНЧ), верхних частот (ФВЧ), полосовые (ПФ) и режекторные (РФ, заграждающие) [2].
Для аппроксимации характеристик фильтров используются специальные типы функций, которые могут быть реализованы в практических схемах. По названию аппроксимирующих функций соответствующие фильтры называю фильтрами Баттерворта, Чебышева, Бесселя, Кауэра и др. [1].
Таким образом, в зависимости от требований, предъявляемых к выходному сигналу, используются те или иные фильтры. И в каждом конкретном случае требуется спроектировать цифровой фильтр с теми или иными характеристиками, удовлетворяющими этим требованиям.
В данной курсовой работе, в соответствии с техническим заданием, проектируется цифрового БИХ-фильтр нижних частот Чебышева 2-го типа.
Все расчеты по проектированию фильтра выполнены в среде MatLab 6.5.
Разработать цифровой БИХ - фильтр нижних частот Чебышева 2-го типа, удовлетворяющий следующим условиям:
§ Граничная частота полосы пропускания – 10 кГц,
§ Граничная частота полосы задерживания– 11 кГц,
§ Минимальное ослабление в полосе задерживания – 60 дБ,
§ Неравномерность передачи в полосе пропускания – 1 дБ,
§ Частота дискретизации – 50 кГц.
Произведем некоторый анализ технического задания.
Проектируемый фильтр должен оперировать с дискретными по времени входными сигналами и иметь бесконечную импульсную характеристику, то есть выходной сигнал фильтра будет определяться не только значениями входного сигнала, но и значениями выходного сигнала в предыдущие моменты времени.
По типу функции, аппроксимирующей исходные характеристики, это будет фильтр Чебышева 2-го типа или инверсный. Вообще фильтры Чебышева обеспечивают более высокую скорость спада АЧХ в переходной полосе, чем, например, фильтры Баттерворта. Кроме того, они обеспечивают монотонное изменение передачи в полосе пропускания и равноволновые пульсации в полосе задерживания [2].
Немало важно, чтобы фильтр был устойчив, а для этого нужно, чтобы его полюса находились в пределах единичной окружности.
Спроектированный фильтр должен быть фильтром нижних частот (ФНЧ), со следующими параметрами: частота среза (частота, отделяющая полосу пропускания от переходной полосы -Fp) должна быть равна 10000Гц, граничная частота полосы задерживания (Fs) должна быть равна 11000Гц, частота дискретизации Ft=50000Гц, минимальное ослабление в полосе задерживания Amin =60 дБ, неравномерность передачи в полосе пропускания Amах=1 дБ. То есть фильтр должен почти без искажений пропускать частотные составляющие в пределах от 0 Гц до 10000 Гц входного сигнала, и практически не должен пропускать остальные.
Спроектированный фильтр должен удовлетворять спецификации, представленной на рис. 1.
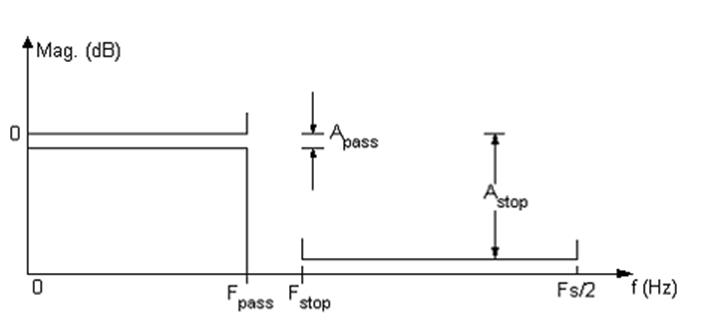
Рис. 1. Спецификация фильтра нижних частот
Расчет БИХ-фильтра заключается в определении значений
коэффициентов ak, bk уравнения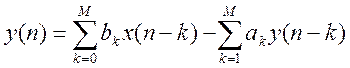 
,
обеспечивающих необходимый вид амплитудной, фазовой или импульсной
характеристик.
Наиболее широко при расчетах БИХ-фильтров используются методы, основанные на использовании аналоговых прототипов фильтров, это так называемые, классические методы. Разработка и применение аналоговых прототипов исторически предшествовали цифровым фильтрам, их методы расчета хорошо развиты. Поэтому наиболее распространены методы расчета БИХ-фильтров, включающие проектирование соответствующего аналогового прототипа, и далее его передаточная функция преобразуется в плоскость z. [1].
Для перехода в z-плоскость используем наиболее часто применяемый метод для расчета ФНЧ - метод билинейного преобразования.
Метод билинейного преобразования
позволяет спроектировать дискретный фильтр по частотной характеристике аналогового прототипа. К достоинствам метода билинейного преобразования относятся простота и качества результирующих характеристик фильтров.
Метод основан на использовании конформного преобразования р-плоскости с помощью функции
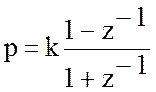(1),
где k– положительная константа.
Соответствие между частотами аналогового фильтра W и w цифрового фильтра следует из подстановки в выражение
(1) 
и, где 
Td– интервал дискретизации. При такой подстановке: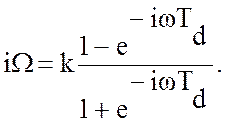 
Эквивалентное выражение
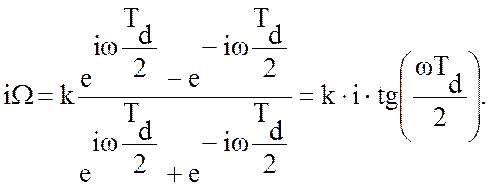
Отсюда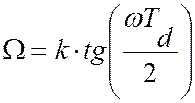 
(2),
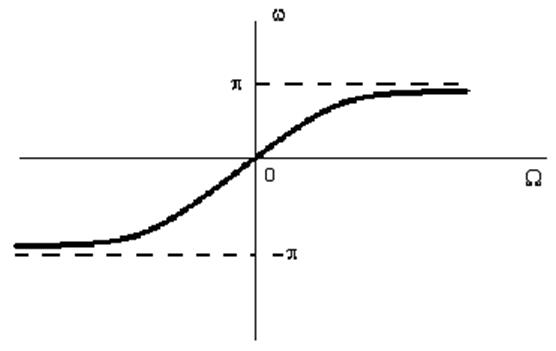
Рис. 2. Связь между частотами аналогового и цифрового фильтров
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
