Разработка цифрового БИХ-фильтра нижних частот Чебышева 2-го типа. Вариант 9, страница 4

F1=filter(n1,d1,s1);

F2=filter(n2,d2,F1);

F3=filter(n3,d3,F2);

F4=filter(n4,d4,F3);

F5=filter(n5,d5,F4);

F6=filter(n6,d6,F5);

F7=filter(n7,d7,F6);

F8=filter(n8,d8,F7);

subplot(2,1,1), plot(i,s1)

title('Signal with frequency 9900 Hz' )

subplot(2,1,2), plot(i,F8)

title('Signal after filtering')

xlabel('N')

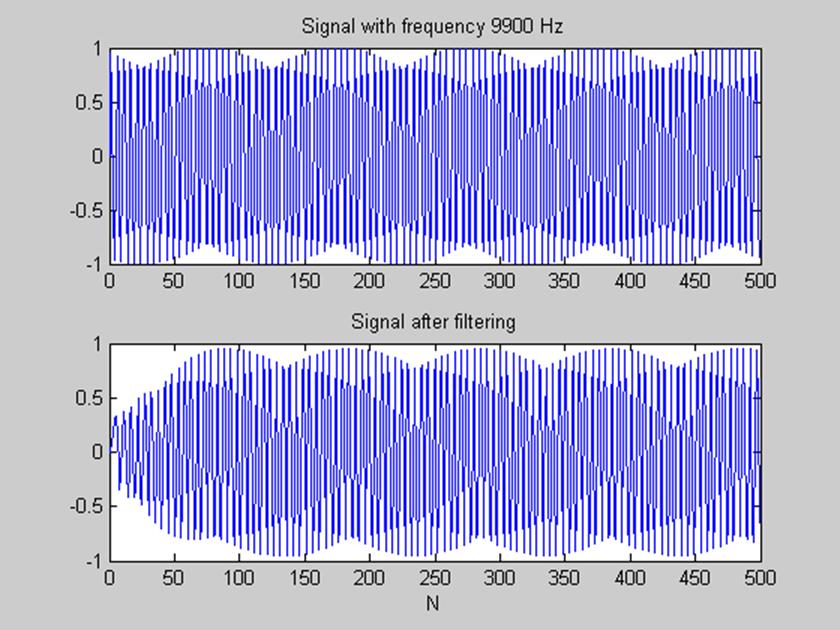
Рис. 15  Фильтрация сигнала с частотой 9900 Гц из полосы пропускания (10000 Гц)

По графикам, представленным на рис.15 видно, что такой сигнал фильтр пропускает без искажений, и лишь вначале может наблюдаться некоторое незначительное ослабление амплитуды выходного сигнала.

б) сигнал с частотой  из полосы задерживания 11500 Гц.

s1=sin(2*pi*11500*Tt*i); %сигнал с частотой из полосы задерживания

F1=filter(n1,d1,s1);

F2=filter(n2,d2,F1);

F3=filter(n3,d3,F2);

F4=filter(n4,d4,F3);

F5=filter(n5,d5,F4);

F6=filter(n6,d6,F5);

F7=filter(n7,d7,F6);

F8=filter(n8,d8,F7);

subplot(2,1,1), plot(i,s1)

title('Signal with frequency 11500 Hz' )

subplot(2,1,2), plot(i,F8)

title('Signal after filtering')

xlabel('N')

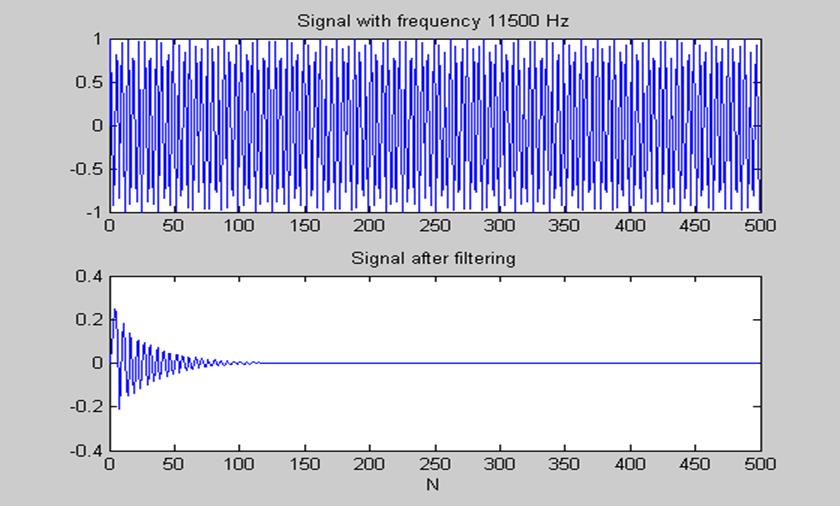
Рис.16  Фильтрация сигнала с частотой 11500 Гц  из полосы  задерживания

Глядя на рис.16, можно сказать, что фильтр практически не пропускает сигнал с частотой из полосы задерживания, как и ожидалось.

в) сигнал с частотой, находящейся в переходной полосе фильтра, 10500 Гц.

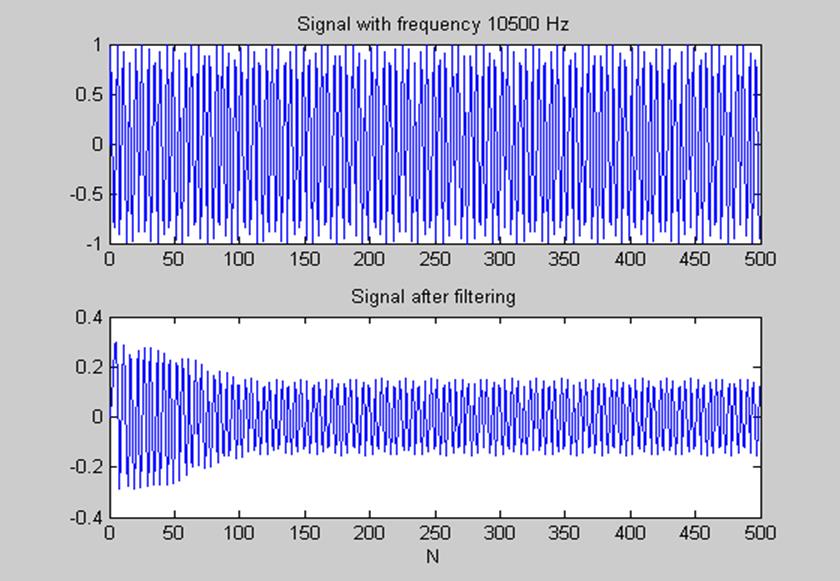
Рис.17  Фильтрация сигнала с частотой 10500 из переходной полосы(10000-11000 Гц)

При подаче на вход фильтра гармоники с частотой из переходной полосы наблюдается сильное ослабление выходного сигнала.

г) сигнал, представляющий собой сумму дискретных гармоник с частотами 11500 Гц (шум) и 9900 Гц (полезный сигнал).

x1=2*cos(2*pi*9900*i*Tt);

x2=2*cos(2*pi*11500*i*Tt);

x=x1+x2;

F1=filter(n1,d1,x);

F2=filter(n2,d2,F1);

F3=filter(n3,d3,F2);

F4=filter(n4,d4,F3);

F5=filter(n5,d5,F4);

F6=filter(n6,d6,F5);

F7=filter(n7,d7,F6);

F8=filter(n8,d8,F7);

subplot(4,1,1), plot(i,x1)

title('Signal with frequency 9900 Hz' )

subplot(4,1,2), plot(i,x2)

title('Signal with frequency 11500 Hz' )

subplot(4,1,3), plot(i,x),axis([0 ,500,-5 ,5 ])

title('Resulting signal'),

subplot(4,1,4), plot(i,F8)

title('Signal after filtering')

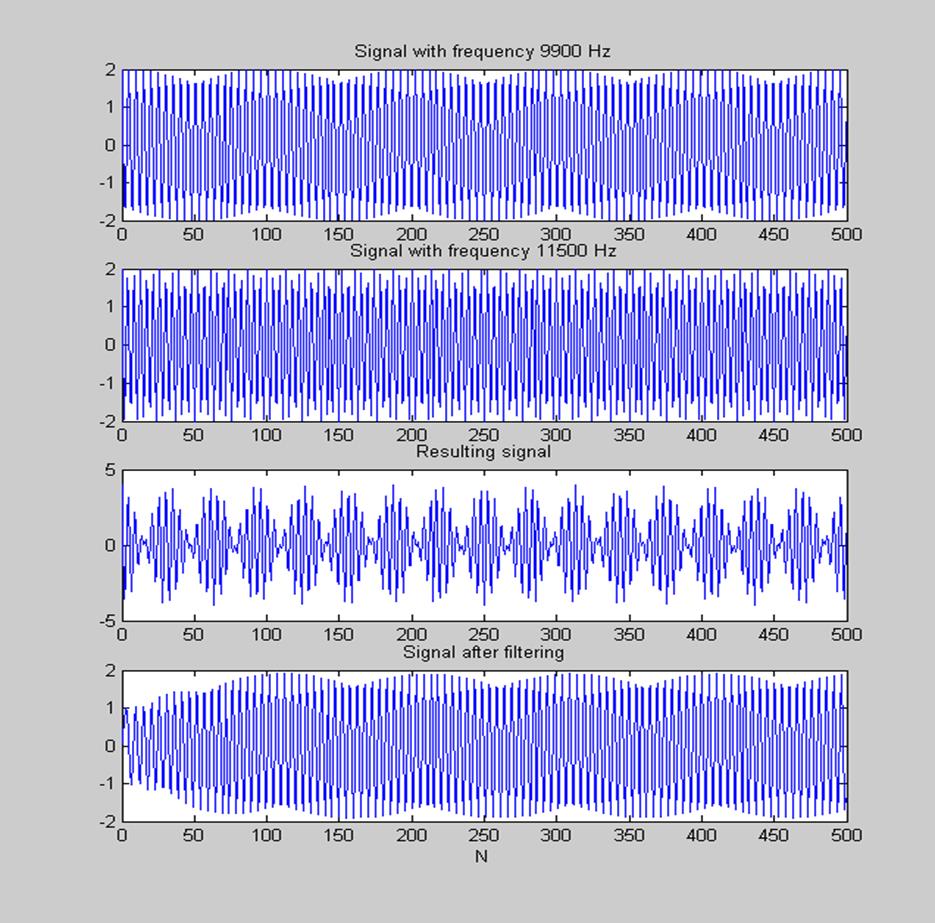
Рис. 18.Сигналы с частотами 9900 и 11500Гц, суммарный сигнал  и сигнал на выходе фильтра

Из графика видно, что фильтр хорошо пропускает низкочастотную составляющую  и подавляет высокочастотные помехи.

По результатам тестирования можно сделать выводы:

фильтр пропускает гармоники сигнала, входящие в полосу пропускания фильтра (0-10000Гц),

с относительно большим ослаблением пропускает гармоники, частоты которых входят в переходную полосу фильтра (от 10000 Гц до 11000 Гц),

практически не пропускает гармоники, входящие в полосу задерживания (от 11000 Гц).

6. Программирование фильтра и оценка быстродействия

Для оценки быстродействия полученного фильтра была разработана программа на языке C++, в качестве компилятора использовался Microsoft Visual C++ 6.0.

Листинг программы:

#include <stdio.h>

#include <iostream.h>

#include <math.h>

#include <windows.h>

#include <conio.h>

#define MAXS 100000     // максимальная размерность массивов входного и выходного сигналов

#define N 20000                 // число отсчетов

int por=2;                            // порядок фильтров для каскадной формы

short b,B,a,A;                    // переменные для вычисления отсчетов выходного сигнала

short pi=3.1415;               

short Fd=20000;                                           

short Td=1/Fd;                                              

short y[MAXS];                // массив для формирования отсчетов выходного сигнала

short x[MAXS];                // массив для формирования отсчетов входного сигнала

short  exit1[MAXS];         // массивы передачи сигнала между элементами

short exit2[MAXS];          // каскадной формы фильтра

short exit3[MAXS];

short exit4[MAXS];

short exit5[MAXS];

short exit6[MAXS];

short exit7[MAXS];

short exit8[MAXS];

short X1[3]={ 0.0129    0.0251  0.0129 }; // коэффициенты   полиномов числителя ПФ фильтра 2-го порядка

short Y1[3]={ 1.0000  0.4920  0.0712}; // коэффициенты полиномов  знаменателя  ПФ фильтра 2-го  порядка

short X2[3]={ 1.0000    1.5602    1.0000 };                             

short Y2[3]={ 1.0000    0.3965    0.1286 };

short X3[3]={ 1.0000    1.0172    1.0000};

short Y3[3]={ 1.0000    0.2323    0.2300 };

short X4[3]={ 1.0000    0.5158    1.0000 };

short Y4[3]={ 1.0000    0.0373    0.3566 };

short X5 [3]={ 1.0000    0.1323    1.0000 };

short Y5[3]={ 1.0000   -0.1555    0.4933 };

short X6[3]={ 1.0000   -0.1310    1.0000 };

short Y6[3]={ 1.0000   -0.3247    0.6320 };

short X7[3]={ 1.0000   -0.2923    1.0000 };

short Y7[3]={ 1.0000   -0.4590    0.7724};

short X8[3]={ 1.0000   -0.3686    1.0000 };

short Y8[3]={ 1.0000   -0.5526    0.9200 };

short OS(short x[],int n, short m1[],short m2[])   // функция расчета выходного сигнала фильтра 2-го порядка

 {                                                                                                                                                                      

for(int i=0;i<por+1;i++)

                                           {

                                                         b=m1[i]*x[n-i];

                                                         B=b+B;

                                           }

                            for(i=1;i<por+1;i++)

                                           {

                                                         a=m2[i]*y[n-i];