Разработка цифрового БИХ-фильтра нижних частот Чебышева 2-го типа. Вариант 9, страница 3

По графику АЧХ видно соответствие граничных частот: Fp=10000 Гц, Fs=11000 Гц (рис.4).

Графики ЛАЧХ  на рис. 7 и 8. показывают, что неравномерность передачи в полосе пропускания составляет не более 1 дБ, а ослабление в полосе задерживания составляет не менее 60 дБ.

Спроектированный  фильтр соответствует  требуемой спецификации.

4.  Реализация фильтра

Цифровые фильтры могут быть реализованы на основе цифрового процессора, позволяющего выполнить алгоритм фильтрации с помощью соответствующей программы, или на базе специализированного цифрового устройства.

Аппаратная реализация цифровых фильтров основана на использовании той или иной формы уравнения или передаточной функции.

Для прямой формы реализации уравнение ЦФ:

.

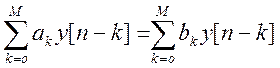Схема, представленная на рис.9 называется прямой формой 1.

Для такой формы реализации характерно избыточное по сравнению с другими формами количество элементов и ярко выраженная чувствительность характеристик фильтра к погрешностям округления коэффициентов [1].

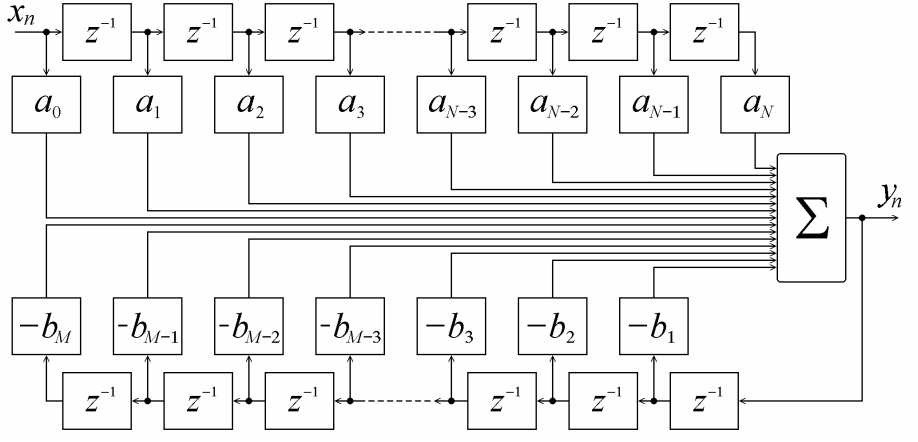
Рис.9. Прямая форма 1 построения ЦФ

На рис.10 изображена вторая прямая форма построения ЦФ (каноническая). По сравнению с формой 1 в ней используется меньшее количество элементов задержки и суммирования [1].

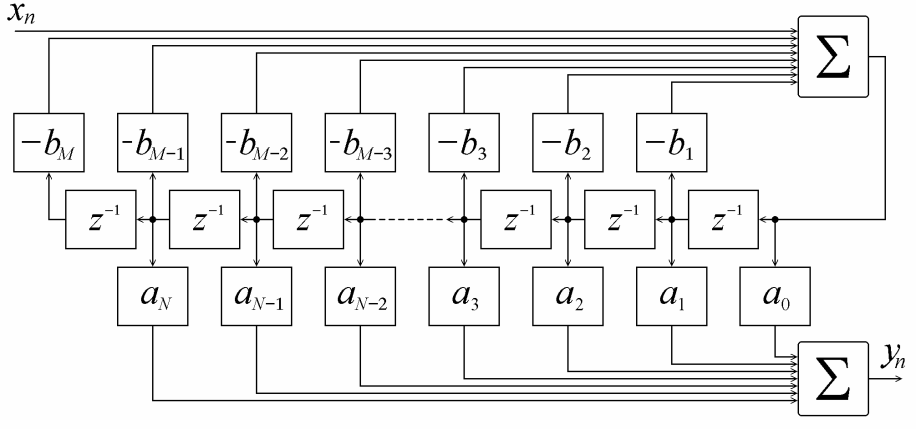
Рис.10. Прямая форма 2 построения ЦФ

Кроме прямых форм выделяют также параллельную и последовательную (каскадную) формы построения ЦФ.

При параллельной реализации функции передачи фильтра  представляется в виде суммы простейших дробей. Каждое из слагаемых при таком представлении соответствует функции передачи рекурсивного фильтра 1-го порядка (возможно, с комплексными коэффициентами) либо 1-го, либо 2-го порядка (если используется представление виде суммы простейших дробей только с вещественными коэффициентами). Сама операция сложения эквивалентна параллельному соединению этих фильтров с суммированием выходных результатов [3].

Для параллельной формы реализации:

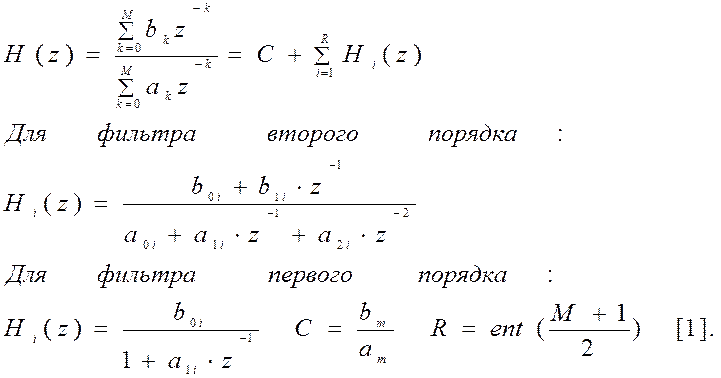
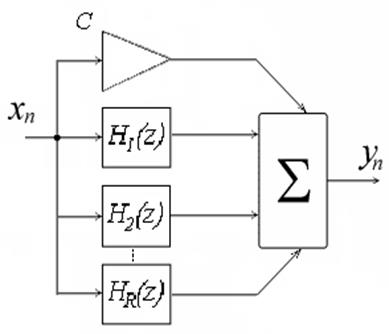
Рис. 11. Структурная схема параллельной формы [4]

Для последовательной формы реализации цифровых фильтров характерна меньшая чувствительность к погрешностям квантования. Числитель и знаменатель функции передачи физически реализуемого дискретного фильтра можно разложить на линейные (относительно z^-1) множители. Перемножение функций передачи соответствует последовательному (каскадному включению) соответствующих фильтров, поэтому такое представление дает реализацию фильтра в виде последовательно включенных фильтров 1-го порядка (при этом некоторые из них могут иметь комплексные коэффициенты) либо фильтров 1-го и 2-го порядка с вещественными коэффициентами [3].

 Для последовательной формы реализации:

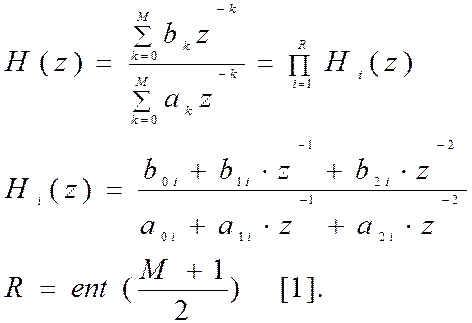
Рис. 12. Структурная схема последовательной формы

В данной работе используется последовательная форма реализации цифрового фильтра, так как она менее чувствительна к погрешностям квантования, возникающим при округлении коэффициентов по сравнению, например, с прямыми формами.

Для осуществления каскадной реализации используем функции:

[z,p,k]=tf2zp(numd, dend);

sos=zp2sos(z,p,k)

Строки матрицы sos содержат коэффициенты фильтров второго порядка

sos =  

    0.0129    0.0251    0.0129    1.0000    0.4920    0.0712

    1.0000    1.5602    1.0000    1.0000    0.3965    0.1286

    1.0000    1.0172    1.0000    1.0000    0.2323    0.2300

    1.0000    0.5158    1.0000    1.0000    0.0373    0.3566

    1.0000    0.1323    1.0000    1.0000   -0.1555    0.4933

    1.0000   -0.1310    1.0000    1.0000   -0.3247    0.6320

    1.0000   -0.2923    1.0000    1.0000   -0.4590    0.7724

    1.0000   -0.3686    1.0000    1.0000   -0.5526    0.9200

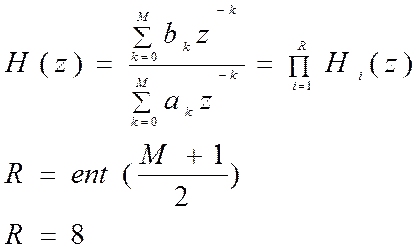
Представим спроектированный фильтр 16-го порядка в виде каскадного соединения восьми фильтров 2-го порядка.

 

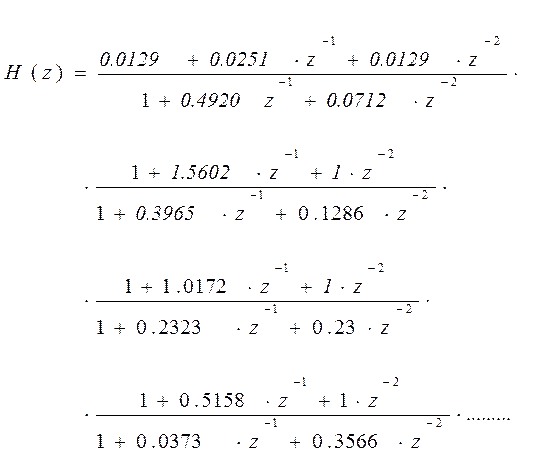
                              Рис. 13. Схема каскадной реализации цифрового БИХ-фильтра НЧ

Чебышева 2-го типа.

Построим графики АЧХ исходного фильтра и фильтра с каскадной реализацией:

[z, p, k]=sos2zp(sos);

[b_q, a_q]=zp2tf(z, p, k);

[H_q, f1]=freqz(b_q, a_q, 256, Ft);

plot(f, abs(H), f1,abs(H_q), '--'), grid

legend('Magnitude response of design filter', 'Magnitude response of cascade filter')

axis([0,25000,0,1.1])

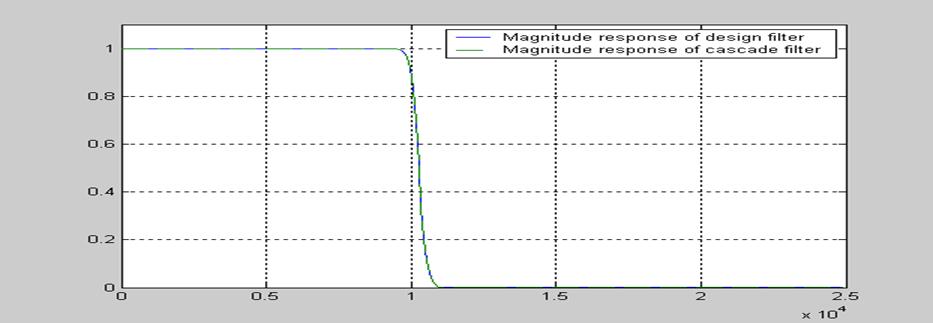
Рис. 14. АЧХ исходного и каскадного фильтров.

Реализация спроектированного фильтра была осуществлена без округления коэффициентов каскадной формы. И как видно из графиков на рис.15, АЧХ исходного и каскадного фильтров совпадают.

5. Тестирование  фильтра

Для проверки работоспособности фильтра проводится процедура тестирования. Необходимо посмотреть действительно ли фильтр пропускает и задерживает частотные составляющие в соответствии с техническим заданием.

Подадим сначала на вход фильтра по отдельности сигналы с частотами в полосе пропускания и в полосе задерживания.

а) сигнал на частоте полосы пропускания, 9900 Гц.

Ft=50000;       % Гц, частота дискретизации

Tt=1/Ft;          % сек, период дискретизации

N=500;

i=0:1:N-1;

n1=[0.0129    0.0251    0.0129];

d1=[1.0000    0.4920    0.0712];

n2=[1.0000    1.5602    1.0000];

d2=[1.0000    0.3965    0.1286];

n3=[1.0000    1.0172    1.0000];

d3=[1.0000    0.2323    0.2300];

n4=[1.0000    0.5158    1.0000];

d4=[1.0000    0.0373    0.3566];

n5=[1.0000    0.1323    1.0000];

d5=[1.0000   -0.1555    0.4933];

n6=[1.0000   -0.1310    1.0000];

d6=[1.0000   -0.3247    0.6320];

n7=[1.0000   -0.2923    1.0000];

d7=[1.0000   -0.4590    0.7724];

n8=[1.0000   -0.3686    1.0000];

d8=[1.0000   -0.5526    0.9200];

s1=sin(2*pi*9900*Tt*i); % сигнал  частоты, входящей в полосу пропускания фильтра