НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Расчетно-графическая работа по курсу
«Теория обработки сигналов»
5 - й семестр
Вариант – 6,7.
Cтудентка: Березикова Н. Преподаватель:
Факультет: АВТ Еленычев С.В.
Группа АО-31
Новосибирск
2005
Раздел1.
1.6. Найдите период сигнала
![]()
Ответ. Период T = π.
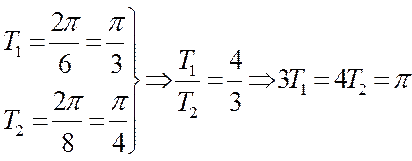
То есть период x(t)=π.
1.7.
Исследуйте характер поведения экспоненциального сигнала дискретного времени ![]() при комплексных значениях
при комплексных значениях ![]() .
.
X[n]= 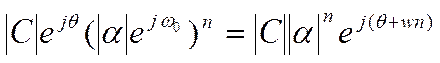
Используя формулу Эйлера ![]() ,
функцию x[n] можно
выразить в виде
,
функцию x[n] можно
выразить в виде
![]()
Если а по модулю меньше единицы, то в области положительных значений n амплитуда функции будет затухающей. В области отрицательных значений n, наоборот – возрастающей. Если а по модулю больше единицы, то функция затухает в области отрицательных значений n, возрастает в положительной области. И действительная, и мнимая части являются затухающими (возрастающими) гармониками.
Изобразим график действительной части для а=e, что >1; ![]() =π/6; w=5; С=1:
=π/6; w=5; С=1:
n=-10:1:10;
x=exp(n).*cos((pi./6)+5*n);
subplot(211);
stem(n,x);
n1=-10:0.05:10;
x1=exp(n1).*cos((pi./6)+5*n1);
subplot(212);
plot(n1,x1);
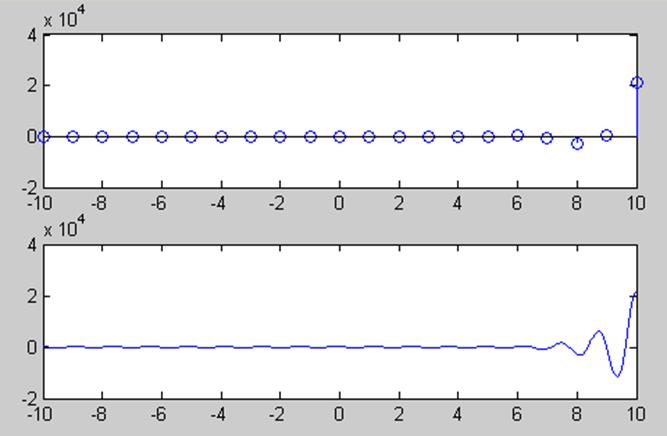
Теперь построим график для а<1, возьмем e-1, остальные данные такие же.
n=-10:1:10;
x=exp(-n).*cos((pi./6)+5*n);
subplot(211);
stem(n,x);
n1=-10:0.05:10;
x1=exp(-n1).*cos((pi./6)+5*n1);
subplot(212);
plot(n1,x1);
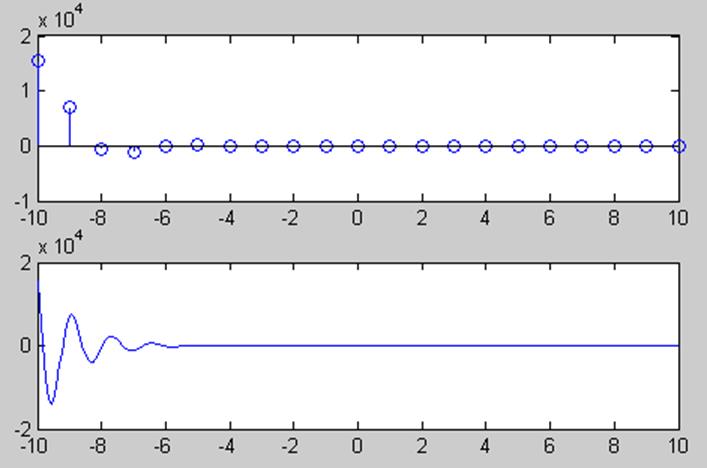
Для каждого случая выведены 2 графика, один из которых является графиком для дискретного времени, а второй выводится для большей наглядности того, что сигнал состоит из возрастающих (затухающих) гармоник действительной и мнимой части (для мнимой гармоникой будет являться синус).
Раздел2.
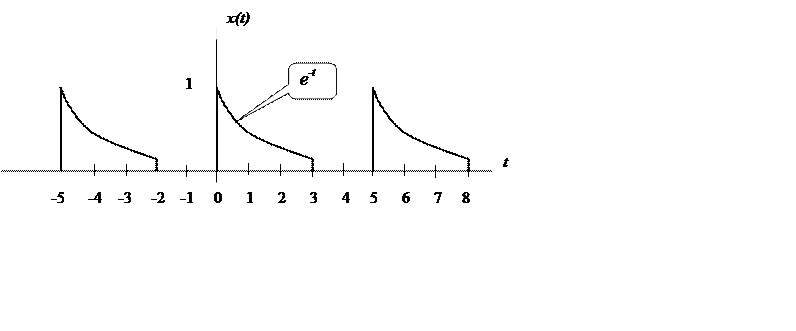 2.6. Определите коэффициенты и
ряд Фурье сигнала
2.6. Определите коэффициенты и
ряд Фурье сигнала
Ответ. 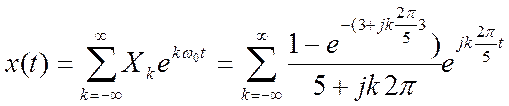
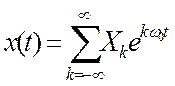
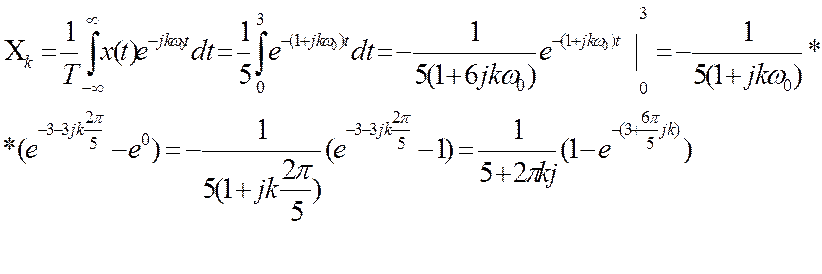
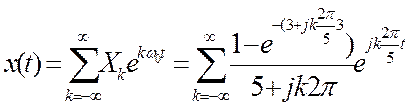
2.7. Определите амплитудный и фазовый спектры периодического сигнала и постройте их графики.
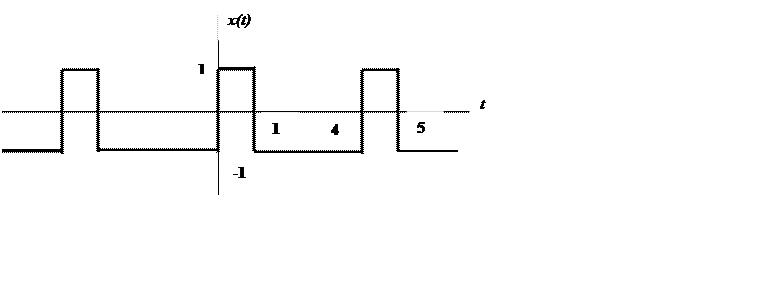 |
Ответ. 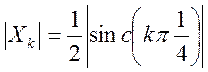 ,
,
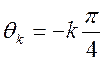
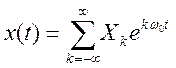
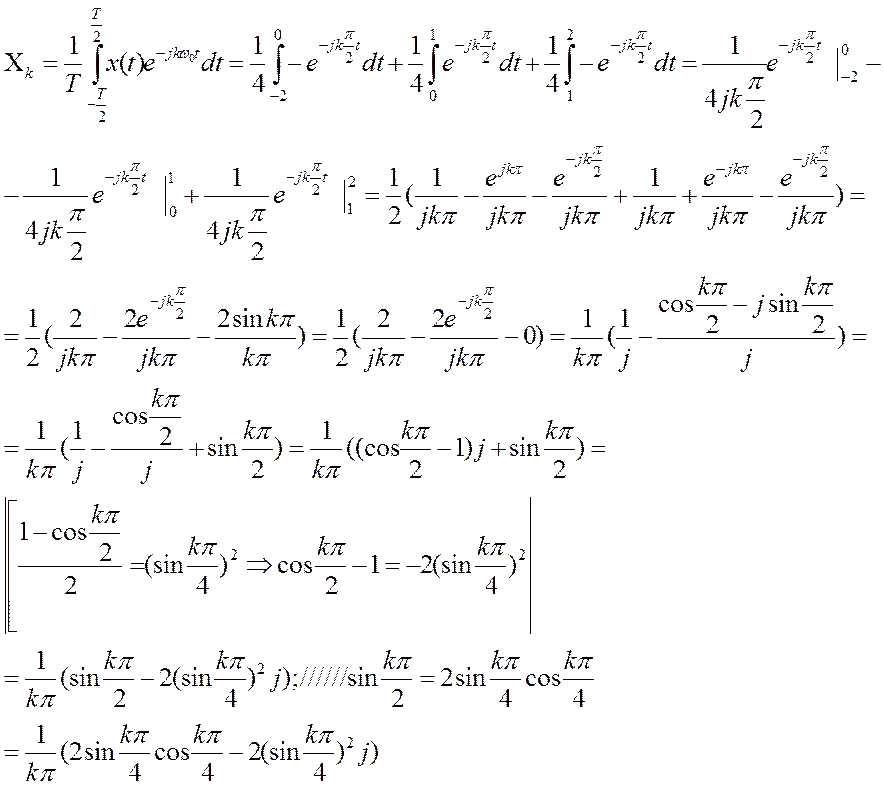
Модуль этого коэффициента равен:
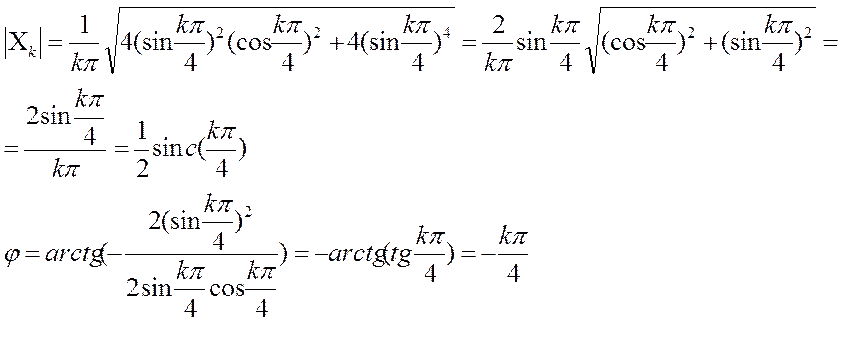
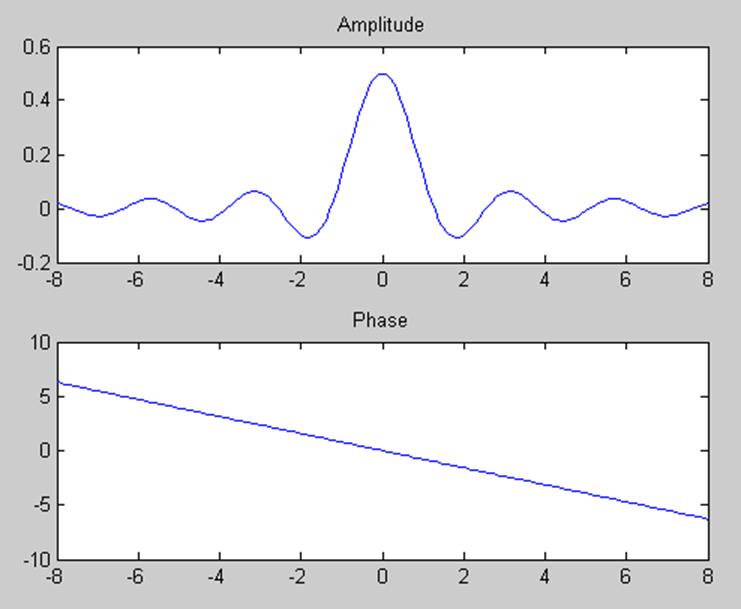
k=-8:0.1:8;
subplot(211);
y=sinc(k*pi./4)./2;
plot(k,y);
title('Amplitude');
f=-k*pi./4;
subplot(212);
plot(k,f);
title('Phase')
Графики для амплитудного и фазового спектров.
Раздел3.
3.6. Найдите преобразование Фурье и постройте график амплитудного спектра сигнала
![]()
Ответ: 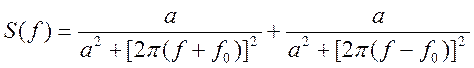
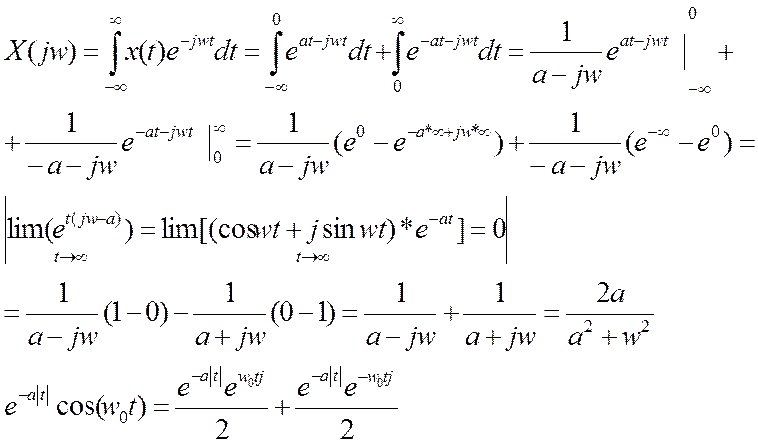
Умножение сигнала на экспоненту, где в степени есть зависимость от времени и мнимого числа во временной области, приведет к сдвигу на w0 в частотной области. Это свойство преобразования Фурье можно применить и в данном примере.
То есть в частотной области преобразование Фурье заданного сигнала будет равно:
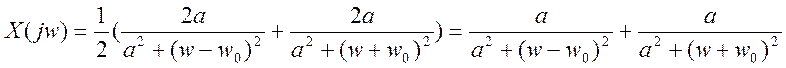
Так как функция является действительной, то она сама будет определять амплитудный спектр, поэтому можно написать такую программу, если присвоить a и w0 какие-то определенные значения, например а=2, w0=1.5:
w=-4*pi:0.01*pi:4*pi;
a=2;
w0=1.5;
x=a./(a.^2+(w-w0).^2);
y=a./(a.^2+(w+w0).^2);
z=x+y;
plot(w,z);
title('Amplitude');
xlabel('Chastota,rad/sec');
ylabel('abs[x(jw)]');
Построим график амплитудного спектра для данных значений а и w0.
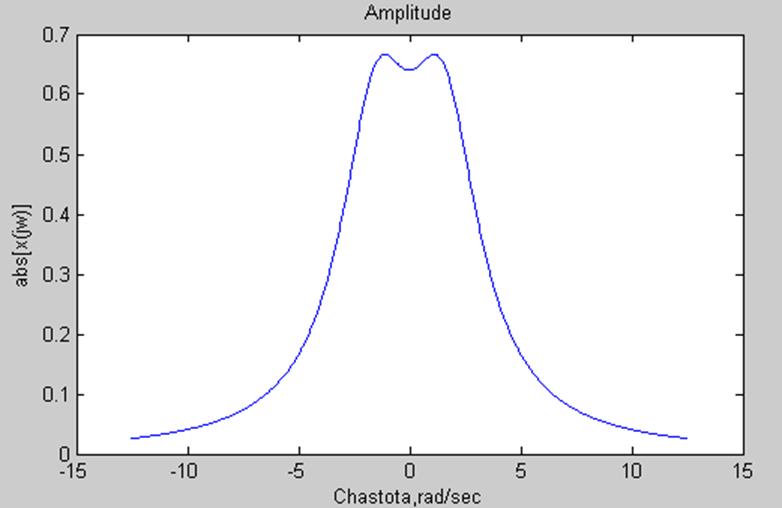
3.7. Дано дифференциальное уравнение, связывающее вход x(t) и выход y(t) системы
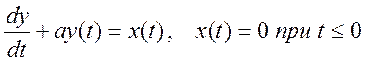 .
.
Найдите преобразование Фурье этого уравнения. Определите отношение
преобразований Фурье левой и правой части, т.е. 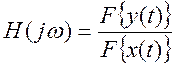 .
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
.
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
Ответ. 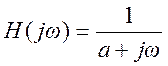 .
.
Преобразование Фурье для y:
![]()
Преобразование Фурье для x:
![]()
![]()
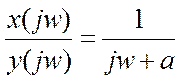
АЧХ:
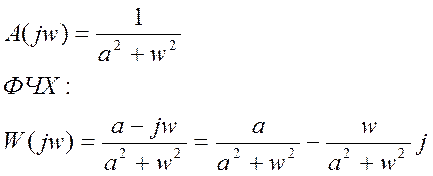
Вещественная часть для a>0 всегда положительна, поэтому:
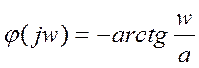
Пусть а=2
w=0:0.1:30;
a=2;
W=(a-w*j)./(a.^2+w.^2);
y=abs(W);
subplot(211);
plot(w,y);
title('Amplitude')
xlabel('Chastota')
subplot(212);
f=angle(W);
plot(w,f);
title('Phase')
xlabel('chastota')
ylabel('Ugol,rad')
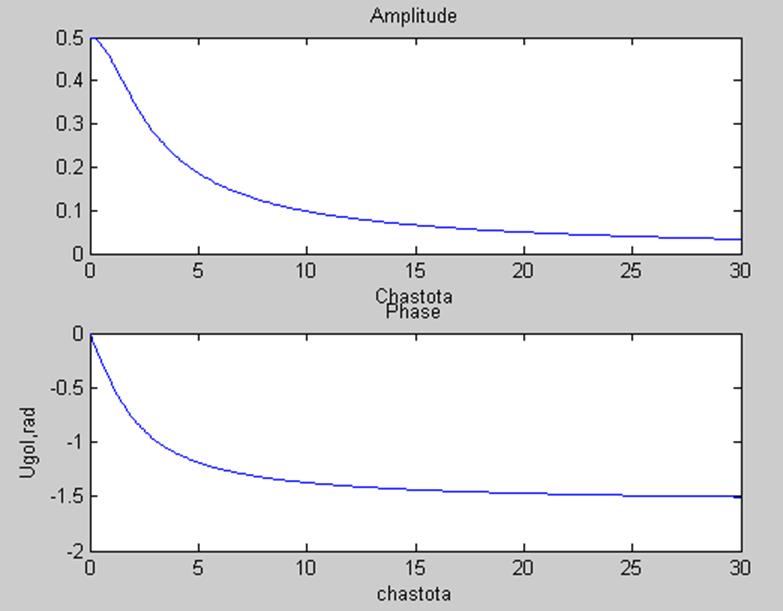
На графиках изображены амплитудный и фазовый спектры. Интерпретацию смысла функций можно показать с помощью рисунка:
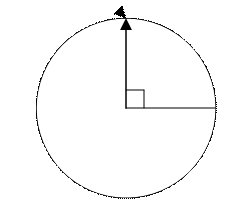
На рисунке показана окружность и стрелка, которая имея какую-либо угловую скорость w может вращаться на угол φ, который определяет фазовый спектр, а ее длину определяет амплитудный спектр. График, который получается в результате «совмещения» двух спектров называется годографом.
Раздел4.
4.6. Докажите, что для
действительной последовательности x[n] амплитудный спектр 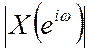 является
четной функцией от ω, а фазовый спектр
является
четной функцией от ω, а фазовый спектр ![]()
- нечетной функцией от ω.
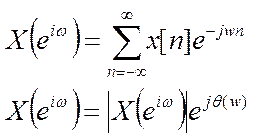
Сигнал x[n] можно представить в виде суммы четной и нечетной составляющей:
X[n]=xe[n]+xo[n], где первая – это четная составляющая, а вторая – нечетная.
Подставим это выражение в первую формулу:
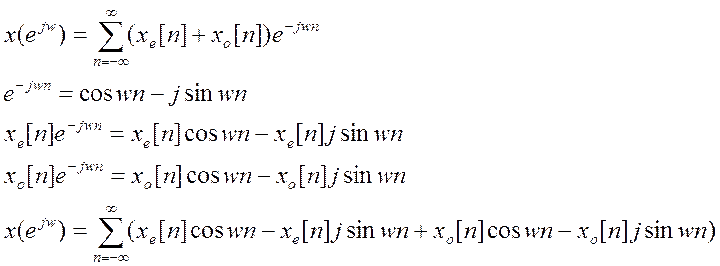
Так как бесконечная сумма нечетной функции равна 0, запишем это равенство в следующем виде:
![]()
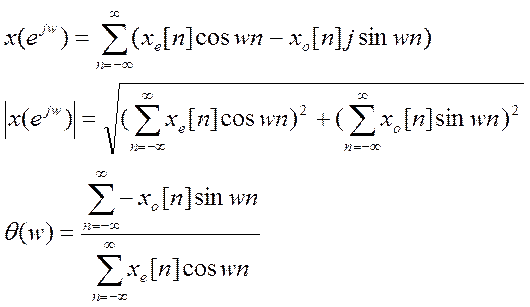
Для амплитудного спектра видно, что под корнем получается четная функция, а значит и сам корень является четной функцией.
Для фазового спектра - так как в сумму числителя входит sin, то функция является нечет.
4.7. Найдите вид сигнала x[n], ДВПФ которого
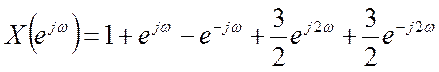 .
.
Ответ. x[-2]=1,5, x[-1]=1, x[0]=1, x[1]= -1, x[2]=1,5.
![]()
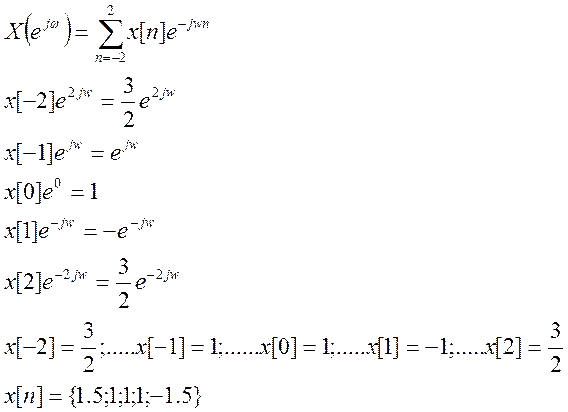
Раздел5.
5.6. Вычислите свертку сигналов
Вычислите свертку сигналов
Изобразите график свертки.
Ответ. 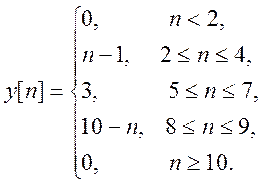
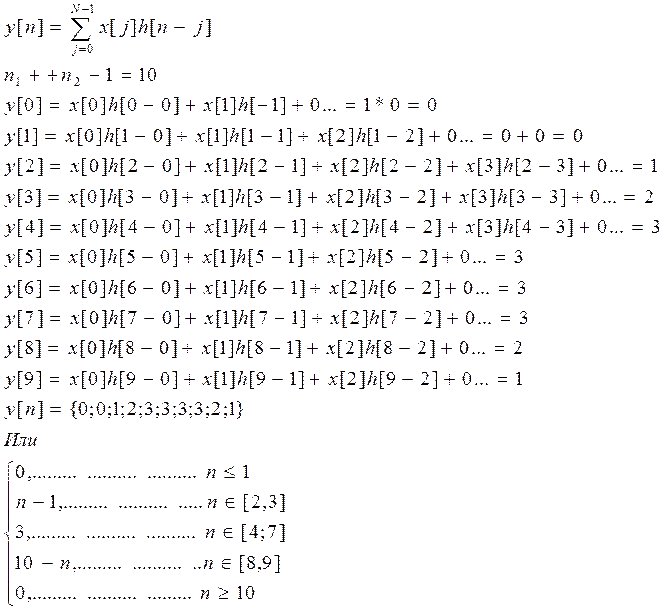
x1=[1 1 1 0 0];
x2=[0 0 1 1 1 1 1 1];
n1=length(x1);
n2=length(x2);
y=conv(x1,x2);
k=1:1:n1+n2-1;
stem(k,y);
Свертка.
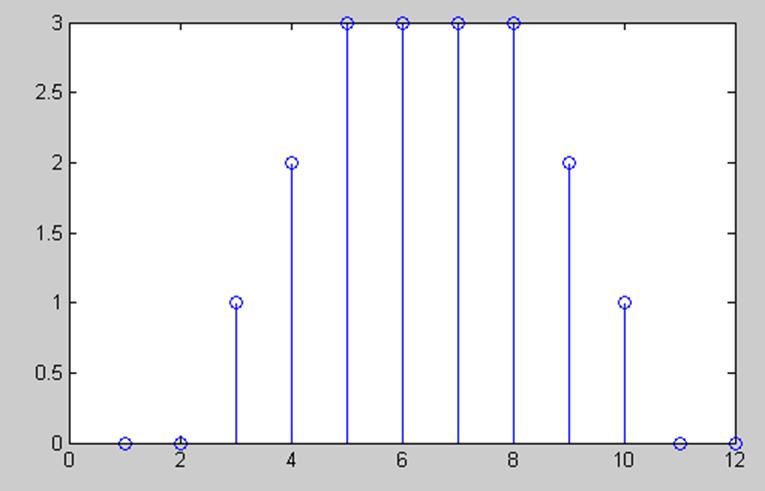
5.7. Вычислите свертку двух
непрерывных сигналов и изобразите её график
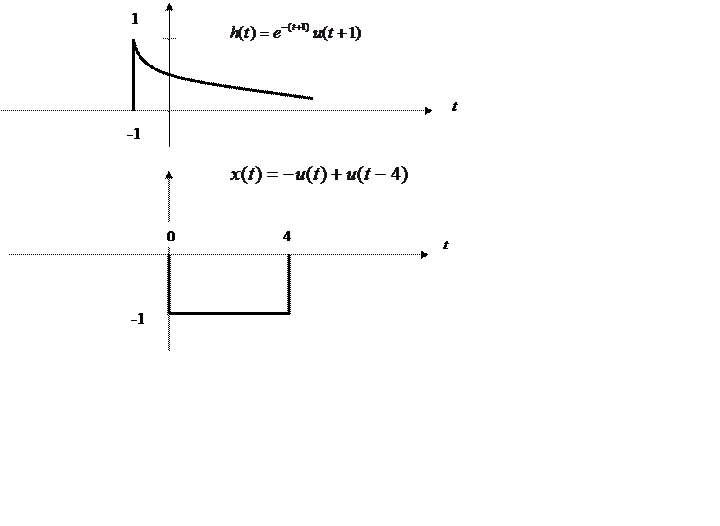 |
Ответ. 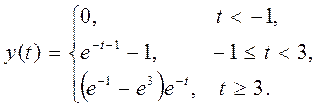
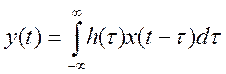
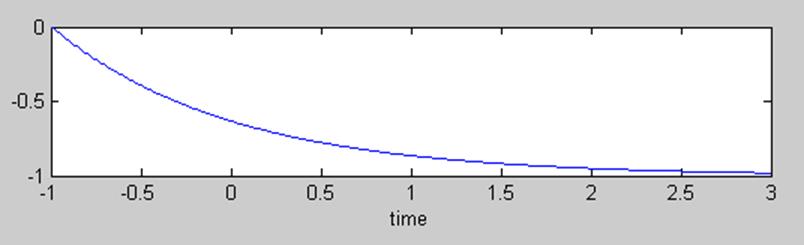
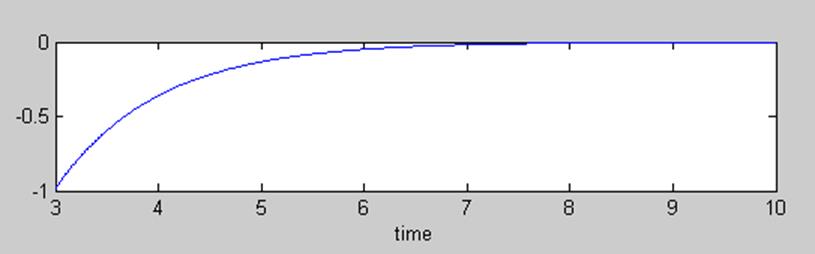
Для данных функций, при зеркальном отображении сигнала x относительно оси ординат, пересечение происходит при значении t=-1. Затем отрезок, на котором происходит пересечение начинает увеличиваться, поэтому пределы интеграла стоит выбрать от -1 и до t. Но с того момента, как t станет равным 3 отрезок пересечения будет постоянным и при t=3 уже стоит брать границы интегрирования такие: от (t-4) и до (t).
То есть
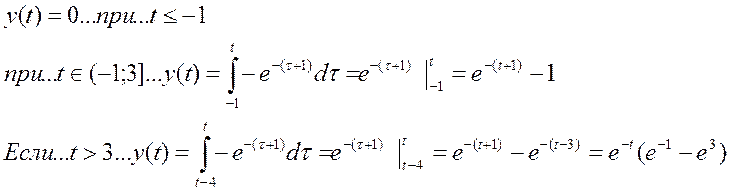
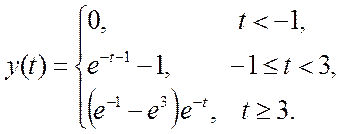
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.