Задачи 7
Лекционный материал - лекции № 15, 16.
1.
Решить следующее неоднородное дифференциальное уравнение второго порядка
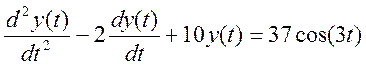 при начальных условиях
при начальных условиях ![]() .
.
Решение.
Решение неоднородного дифференциального уравнения равно сумме общего решения
соответствующего однородного уравнения yc(t) (общего интеграла) и частного решения (частного
интеграла) yp(t).
Вначале находим общее решение однородного ДУ. Составляем характеристическое
уравнение ![]() , определяем его корни
, определяем его корни ![]() . Поскольку это характеристическое
уравнение имеет пару однократных комплексно сопряженных корней вида
. Поскольку это характеристическое
уравнение имеет пару однократных комплексно сопряженных корней вида ![]() , то общий интеграл уравнения имеет
вид
, то общий интеграл уравнения имеет
вид ![]() . Для данного случая
. Для данного случая ![]() .
.
Произвольные постоянные C1
и C2 определяем по начальным
условиям. Исходя из начальных условий, получаем следующую систему уравнений
для C1 и C2
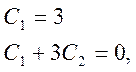
из которой находим C1=3 и C2=-1. Поэтому общее решение ДУ ![]() .
.
Частное решение уравнения определяем соответственно его
правой части ![]() . При правой части уравнения
вида
. При правой части уравнения
вида ![]() частное решение есть функция, отличающаяся
от x(t) только
числовыми коэффициентами. В данном случае a=0, b=3 и поскольку числа
частное решение есть функция, отличающаяся
от x(t) только
числовыми коэффициентами. В данном случае a=0, b=3 и поскольку числа ![]() не
являются корнями характеристического уравнения, то частный интеграл записываем
в виде
не
являются корнями характеристического уравнения, то частный интеграл записываем
в виде ![]() . Определяем производные первого и
второго порядков этой функции
. Определяем производные первого и
второго порядков этой функции
![]() .
.
Подставляем выражения ![]() в исходное
неоднородное ДУ и получаем равенство
в исходное
неоднородное ДУ и получаем равенство ![]() .
Это равенство будет тождеством при равенстве коэффициентов у
.
Это равенство будет тождеством при равенстве коэффициентов у ![]() в левой и правой части, т.е. когда
в левой и правой части, т.е. когда
![]()
Решая эту систему, находим A = 1, B = -6. Следовательно,
![]() .
.
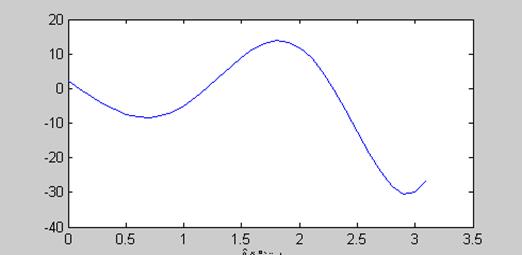
Таким образом, решение данного уравнения
![]() . График решения
. График решения
2.
Является ли линейной и инвариантной во времени (стационарной) система с
уравнением выход – вход
а) ![]()
б) ![]() ?
?
Решение.
а) Для входных сигналов x1(t) и x2(t) выход
соответственно ![]() . Если входной сигнал
. Если входной сигнал ![]() , то выход
, то выход
![]() .
Система удовлетворяет принципу суперпозиции, следовательно, - линейная.
.
Система удовлетворяет принципу суперпозиции, следовательно, - линейная.
Положим вход системы
в виде ![]() , при этом выход
, при этом выход ![]() . Поскольку
. Поскольку ![]() ,
то система – неинвариантная во времени (нестационарная).
,
то система – неинвариантная во времени (нестационарная).
б) Система с уравнением ![]() . Для входных сигналов x1(t) и x2(t) выходные
сигналы
. Для входных сигналов x1(t) и x2(t) выходные
сигналы ![]() и
и ![]() .
Для линейной комбинации входных сигналов
.
Для линейной комбинации входных сигналов ![]() выход
выход
![]() , поэтому система – линейная.
, поэтому система – линейная.
Система – стационарная, так как
![]()
3. Найти
импульсную характеристику (ИХ) системы с уравнением
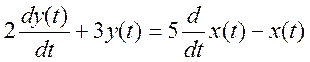 .
.
Решение.
Для определения ИХ h(t) системы будем использовать метод, основанной на нахождении
переходной характеристики g(t)
системы и использовании простой связи между импульсной и переходной
характеристиками, т.е. 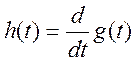 . Переходная
характеристика системы будет определяться, как решение дифференциального уравнения
системы при правой части
. Переходная
характеристика системы будет определяться, как решение дифференциального уравнения
системы при правой части 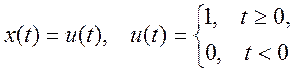 , где u(t) -функция единичного
скачка.
, где u(t) -функция единичного
скачка.
Запишем левую часть исходного уравнения с правой частью u(t)
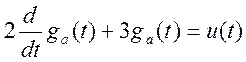 .
(*)
.
(*)
Характеристическое уравнение ![]() . Его корень
. Его корень ![]() .
.
Следовательно, решение однородного уравнения (*) ![]() .
.
Найдем частное решение уравнения (*) при правой части ![]() . При этом исходим из теоретических
положений, определяющих, что для правой части ДУ в виде
. При этом исходим из теоретических
положений, определяющих, что для правой части ДУ в виде ![]() ,
где P(t) – многочлен,
частное решение yp(t) отличается от f(t) только числовыми коэффициентами – константами. Для f(t)=u(t) частное решение будет иметь вид
,
где P(t) – многочлен,
частное решение yp(t) отличается от f(t) только числовыми коэффициентами – константами. Для f(t)=u(t) частное решение будет иметь вид ![]() . Подставим yp(t) в уравнение (*), получим уравнение
. Подставим yp(t) в уравнение (*), получим уравнение
![]() , отсюда
, отсюда 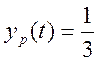 .
Складывая общее решение однородного уравнения и частное решения уравнения (*),
находим решение в виде
.
Складывая общее решение однородного уравнения и частное решения уравнения (*),
находим решение в виде
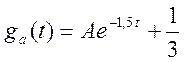 . Для определения значения константы A используем нулевые начальные
условия, характерные для получения переходной характеристики, а именно:
. Для определения значения константы A используем нулевые начальные
условия, характерные для получения переходной характеристики, а именно:
t = 0- ga(0-)=0.
Поэтому 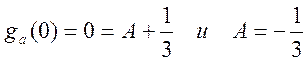 . Следовательно,
. Следовательно, 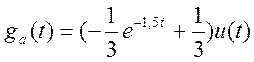 . Дифференцируя ga(t), получаем
промежуточную составляющую искомой импульсной характеристики.
. Дифференцируя ga(t), получаем
промежуточную составляющую искомой импульсной характеристики.
Подставим выражение ha(t) в правую часть дифференциального уравнения системы для
определения окончательного вида ИХ системы
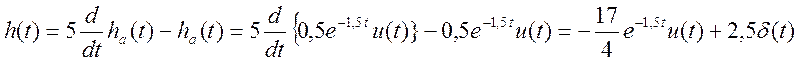 .
.
В этом выражении ![]() - это дельта-функция,
возникающая из-за наличия в правой части исходного уравнения системы
производной входного сигнала
- это дельта-функция,
возникающая из-за наличия в правой части исходного уравнения системы
производной входного сигнала 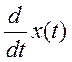 . При этом появляется
необходимость дифференцирования
. При этом появляется
необходимость дифференцирования 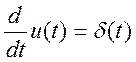 . Если в правой
части исходного уравнения не будет производной, то и дельта – функции в выражении
ИХ не будет.
. Если в правой
части исходного уравнения не будет производной, то и дельта – функции в выражении
ИХ не будет.
4. Получить
дифференциальное уравнение, передаточную функцию, частотные характеристики,
нули и полюса электрической цепи
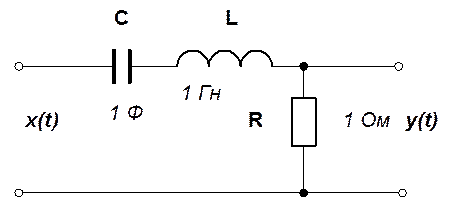
Решение.
![]() , выразим ток в цепи через
выходное напряжение
, выразим ток в цепи через
выходное напряжение 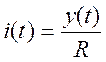 ,
,
при этом 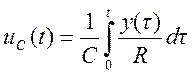 ,
, 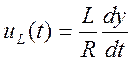 . Уравнение системы
. Уравнение системы
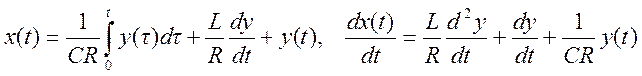 .
.
Для указанных в условии номинальных значений элементов 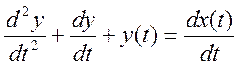 .
.
Передаточная функция: возьмем преобразование Лапласа от обеих частей уравнения
![]() ,
, 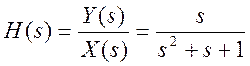 .
.
Нуль передаточной функции z = 0,
полюса 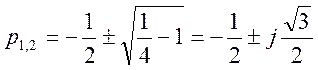
Частотная характеристика цепи
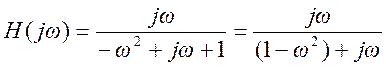 .
.
Амплитудно – частотная характеристика 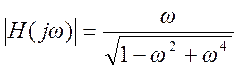 .
.
Фазо – частотная характеристика ![]() .
.
Графики
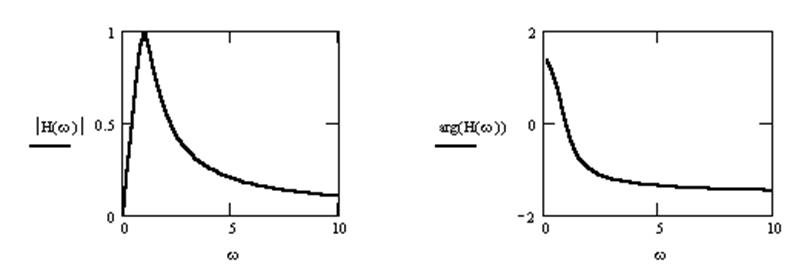
Вид АЧХ свидетельствует, что цепь представляет собой полосовой фильтр.
5.
Найти выходной сигнал RC – цепи первого
порядка, на вход которой поступает прямоугольный импульс x(t) с амплитудой А и длительностью tи.

Решение.
Импульсная характеристика цепи 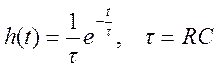 .
.
Запишем прямоугольный импульс в виде разности единичных ступенчатых функций
![]() .
.
Выходной сигнал цепи
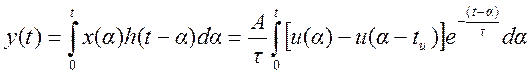 ,
,
для ![]()
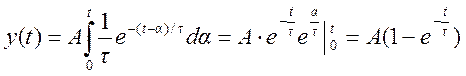 ,
,
для ![]()
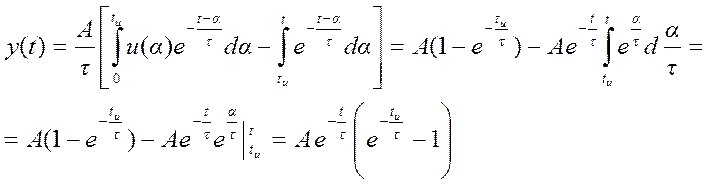
Второй, более простой вариант решения.
Переходная характеристика цепи
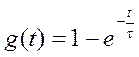 , для
, для ![]()
![]()
Для ![]()
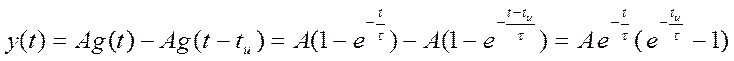
График для A=5, τ = 0,5 , tи = 5
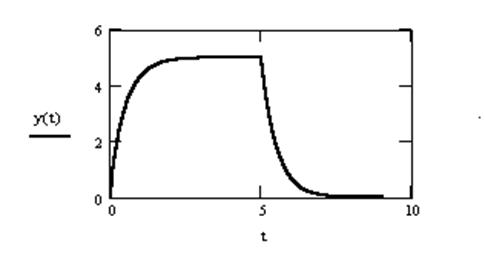
6. 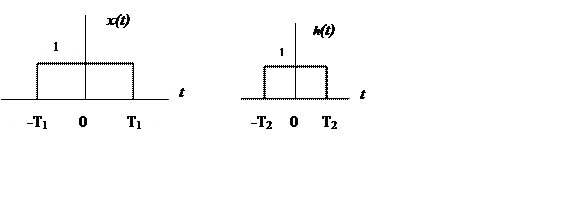 Вычислить
свертку сигналов
Вычислить
свертку сигналов
Решение.
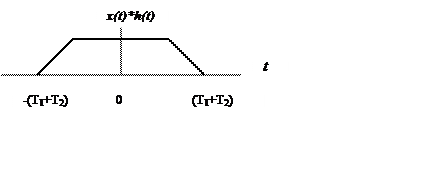
Воспользуемся геометрической трактовкой свертки: зеркальное отображение, сдвиг, перемножение, интегрирование.
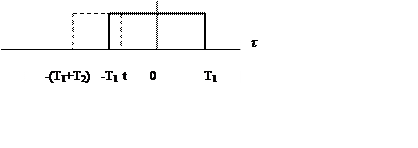
Если ![]() , то h(-τ) не будет перекрываться с x(τ) и их произведение и интеграл равен нулю. Когда
, то h(-τ) не будет перекрываться с x(τ) и их произведение и интеграл равен нулю. Когда ![]() площадь совместного перекрытия
сигналов линейно увеличивается (уменьшается) и интеграл свертки линейно растет
(убывает), в интервале
площадь совместного перекрытия
сигналов линейно увеличивается (уменьшается) и интеграл свертки линейно растет
(убывает), в интервале ![]() площадь перекрытия функций
не изменяется при смещении t и
интеграл свертки – константа.
площадь перекрытия функций
не изменяется при смещении t и
интеграл свертки – константа.
7.
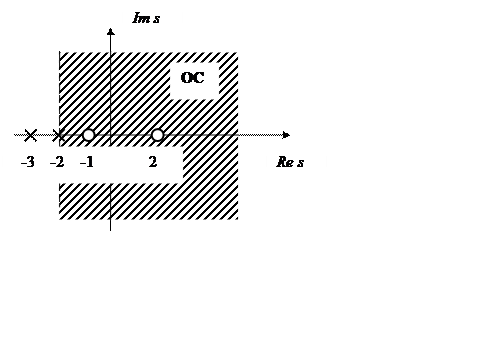
Задана передаточная функция системы 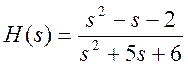 .
Найти область сходимости (ОС) передаточной функции, её полюса и нули и
импульсную характеристику системы.
.
Найти область сходимости (ОС) передаточной функции, её полюса и нули и
импульсную характеристику системы.
Решение.
Найдем нули и полюса системы
Нули ![]() ,
,
 Полюса
Полюса ![]()
Полюсно - нулевое представление передаточной функции
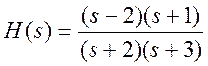 .
.
Расположение полюсов, нулей и области сходимости передаточной функции
Разложим передаточную функцию на простые дроби для упрощения перехода во временную
область (вычисление обратного преобразования Лапласа от передаточной функции
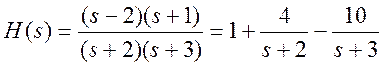 .
.
Обратные преобразования Лапласа 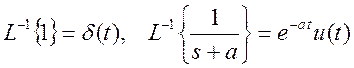 .
.
Поэтому импульсная характеристика системы ![]()
8.
Задана частотная характеристика системы 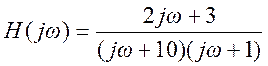 .
Найти её импульсную характеристику.
.
Найти её импульсную характеристику.
Решение.
Запишем H(jω) в виде суммы элементарных дробей 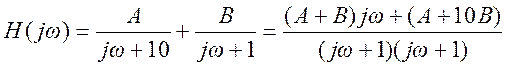
Приравнивая коэффициенты при соответствующих степенях jω числителя H(jω), получаем
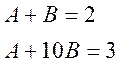 Решая, получим
Решая, получим 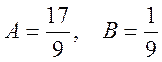 .
.
Отсюда
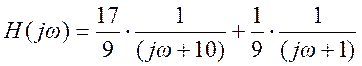 .
.
Обратное преобразование Фурье 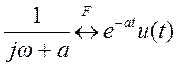 ,
поэтому импульсная характеристика
,
поэтому импульсная характеристика
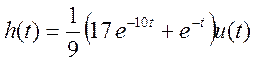
9. Задана
система с передаточной функцией 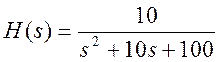 .
.
Найти полюса системы, определить
отклик системы в установившемся состоянии на гармонический входной сигнал ![]()
Решение.
Полюса системы ![]()
Отклик системы H(s) на гармонический
вход ![]() есть
есть
![]() .
.
При ![]() частотная
характеристика для ω = 10
частотная
характеристика для ω = 10
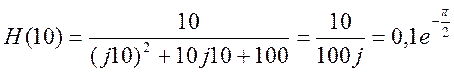 ,
поэтому
,
поэтому
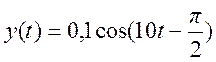
10. Система состоит из
последовательного соединения двух систем

Первая система имеет импульсную характеристику ![]() . Для второй системы известно, что
входному сигналу
. Для второй системы известно, что
входному сигналу ![]() соответствует выходной
сигнал
соответствует выходной
сигнал
![]() . Найти
. Найти
а) частотную характеристику всей системы,
б) дифференциальное уравнение системы,
в) Импульсную
характеристику всей системы.
Решение.
Для последовательного соединения систем частотная характеристика ![]() .
.
Частотная характеристика первой системы 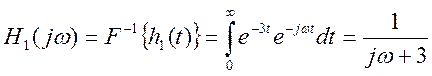 .
.
Для второй системы связь выхода и входа в частотной области ![]() .
.
Частотный спектр выходного сигнала для заданного y(t)
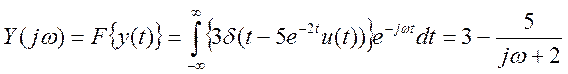 . Частотный спектр
входного сигнала системы 2
. Частотный спектр
входного сигнала системы 2 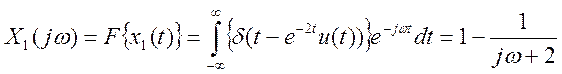 .
.
Найденные выражения спектров
позволяют определить частотную характеристику системы 2 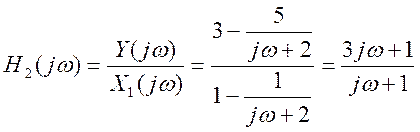 .
.
Частотная характеристика всей системы 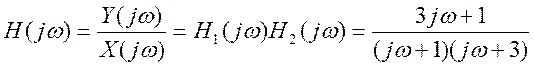 .
.
Отсюда связь выход – вход в частотной области для всей системы
![]() .
.
По теореме дифференцирования
преобразования Фурье
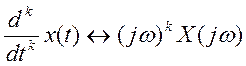 .
.
Применяя это свойство к каждому
члену предыдущего выражения, получаем дифференциальное уравнение системы
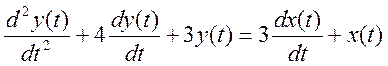 .
.
Для получения импульсной характеристики представим H(jω) в виде суммы простых дробей 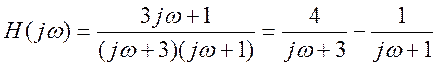 .
.
Беря обратное преобразование Фурье от каждой дроби частотной характеристики,
получаем импульсную характеристику системы
![]() .
.
Задачи для самостоятельного решения
1. Определите,
является ли линейной и стационарной (инвариантной во времени) система с
уравнением
а) ![]() ,
,
б) ![]() ?
?
Ответ. а) Система линейная и нестационарная, б) система –
нелинейная и стационарная

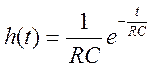 .
.4. Система имеет переходную характеристику вида
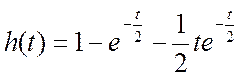 .
.
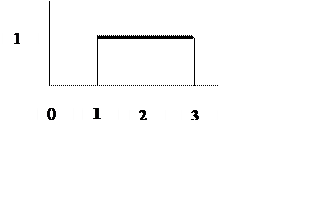 На
вход системы подается сигнал вида
На
вход системы подается сигнал вида
Определите выходной сигнал системы.
Ответ.
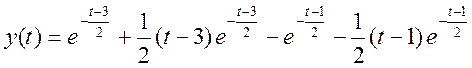 .
.
5. Определите передаточную функцию, полюса, АЧХ и ФЧХ RLC – цепи, изображенной на рис.
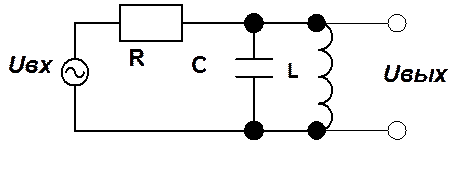
Ответ. 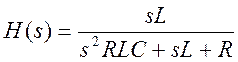
5. Дифференциальное уравнение фильтра нижних частот (ФНЧ)
второго порядка Баттерворта имеет вид
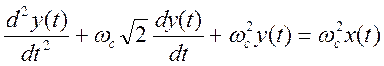 , где ωс –частота среза
фильтра.
, где ωс –частота среза
фильтра.
Найдите частотную характеристику фильтра и его АЧХ, постройте график АЧХ.
Ответ. 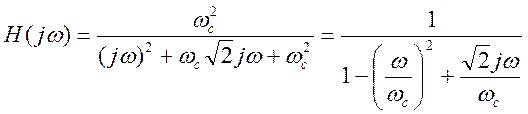
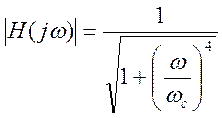
6. Ниже представлены две диаграммы нулей и полюсов системы
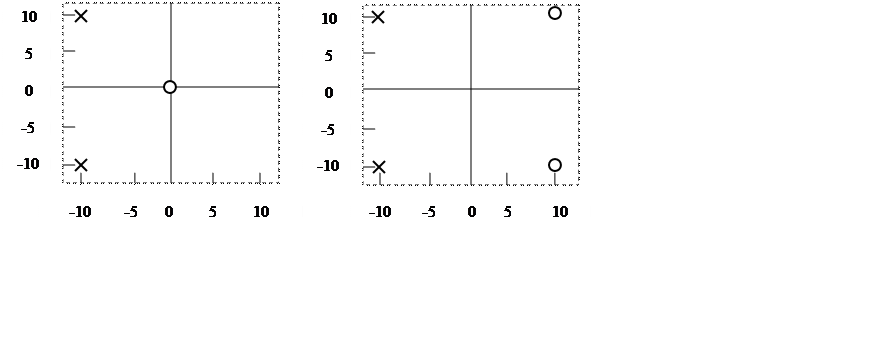
Запишите выражения передаточной функции систем.
Ответ. а) 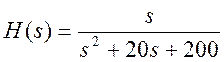 ,
б)
,
б) 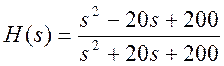 .
.
7. Передаточная
функция системы имеет вид
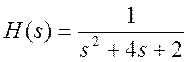 . Найдите полюса системы. Является
ли система устойчивой?
. Найдите полюса системы. Является
ли система устойчивой?
Определите отклик системы на входной сигнал ![]() .
.
Ответ. ![]() .
. ![]()
8.
Найдите выходной сигнал системы с импульсной характеристикой ![]() и входным сигналом
и входным сигналом ![]() .
.
Ответ. ![]()
9.
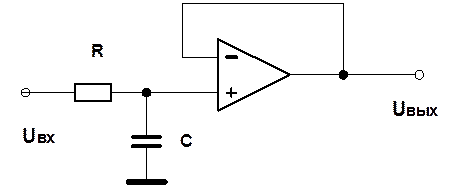 Для цепи, изображенной на рис., определите передаточную функцию,
частотные характеристики, импульсную характеристику. Операционный усилитель
считайте идеальным
Для цепи, изображенной на рис., определите передаточную функцию,
частотные характеристики, импульсную характеристику. Операционный усилитель
считайте идеальным
Ответ. 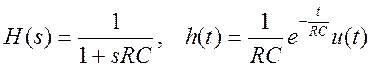
10.
Линейная непрерывная стационарная система
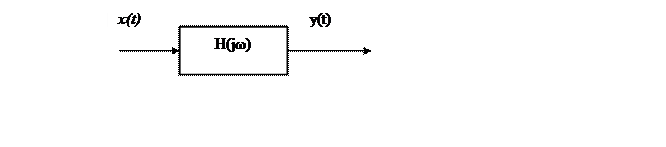
имеет входной сигнал 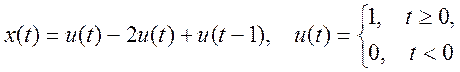 .
.
При этом выходной сигнал ![]() .
.
Постройте графики входного и выходного сигналов, определите преобразование Фурье (спектр) выходного сигнала y(t), найдите частотную характеристику системы.
Ответ. ![]()
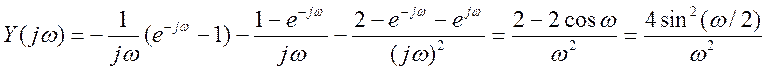
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.