Министерство образования РФ
Новосибирский Государственный Технический Университет
Кафедра Систем Сбора и Обработки Данных
Курсовая работа по предмету ТОС.
«Разработка эллиптического ФНЧ»
Факультет: АВТ
Группа: АО-81
Студент: Киселев М.Н. Преподаватель: Щетинин Ю.И.
Вариант: 22.
Новосибирск, 2001.
Содержание
Техническое задание................................................... 3
Введение............................................................................... 4
1. Определение порядка ФНЧ-прототипа......................................... 5
2. Определение коэффициентов уравнения ФНЧ-прототипа...... 5
3. Определение передаточной функции............................................ 5
4. Получение цифрового фильтра с заданными характеристиками.................................................................................. 7
6. Проверка работоспособности фильтра....................................... 10
Заключение...................................................................... 12
Литература........................................................................ 13
Разработать эллиптический фильтр нижних частот со следующими характеристиками:
![]()
![]() Пульсации в
полосе задерживания не менее дБ.
Пульсации в
полосе задерживания не менее дБ.
![]() Пульсации в полосе пропускания не более дБ.
Пульсации в полосе пропускания не более дБ.
fs1 = 200Гц – граничная частота среза полосы пропускания
fs2 = 230Гц – граничная частота среза полосы задерживания
Существует большое разнообразие фильтров. Они классифицируются по разным параметрам. Например, по типу обрабатываемого сигнала фильтры бывают аналоговые и цифровые; по виду их АЧХ (по частотам пропускания и заграждения) бывают ФНЧ (низких частот), ФВЧ (высоких частот), ПФ (полосовые) и РФ (режекторные); по типу аппроксимирующей функции фильтры бывают: Баттерворта, Чебышева (равноволновые), Бесселя, Кауэра (эллиптические) и др.
Встречаются обстоятельства, когда желательно иметь конечные нули передачи. В 1931 году Кауэр показал, что можно получить гораздо лучшую аппроксимацию идеализированных амплитудно-частотных характеристик фильтров нижних частот, если использовать фильтр с конечными нулями передачи. Он нашел, что при надлежащем выборе нулей и полюсов можно спроектировать фильтр с разноволновым затуханием как в полосе затухания, так и полосе задерживания. Поскольку координаты нулей в таких фильтрах определяются эллиптическими функциями классической теории поля, эти фильтры часто называют эллиптическими. Другое их название – фильтры Кауэра, поскольку впервые их описание появилось в работе Кауэра.
Эллиптический фильтр имеет амплитудно-частотную характеристику, которая содержит пульсации как в полосе пропускания, так и в полосе задерживания и является лучшим среди всех фильтров нижних частот в том смысле, что для заданного порядка и допустимых отклонений характеристики в полосах пропускания и задерживания обладает самой узкой шириной переходной области.
В данной работе будет разработан эллиптический фильтр и продемонстрированы его преимущества.
Постоянные параметры А, В, С
для расчета эллиптического фильтра вычисляются крайне сложно. Этот процесс
требует знаний эллиптический функций Якоби. Поэтому, в данной работе, эти
коэффициенты берутся из таблицы [1, стр. 82].
Расчет
фильтра
Исходя из значений технического задания, а именно пульсаций в полосе задерживания и пульсаций в полосе пропускания по монограмме определяем порядок эллиптического фильтра. По графику он получается около 9.4
Так как порядок фильтра должен быть целым числом, а по монограмме определяется минимальное значение порядка, нужного для реализации фильтра с заданными характеристиками, то округляем n до 10.
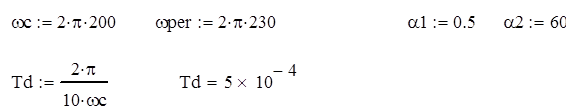 |
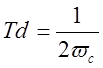
Определяем нормируемую границу полосы задерживания.
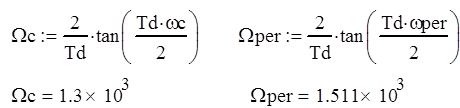 |
Коэффициенты берутся из таблицы для данных [1, стр. 82], соответствующих заданным значениям пульсаций для порядка 10.
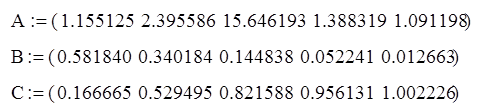
Из справочника возьмем формулу, описывающую эллиптический фильтр n-го порядка. Если
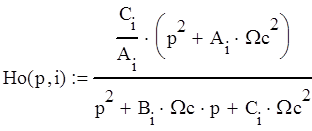
есть передаточная функция 2-го порядка [1, стр.68], то передаточная функция 10-го порядка будет выглядеть так:
![]()
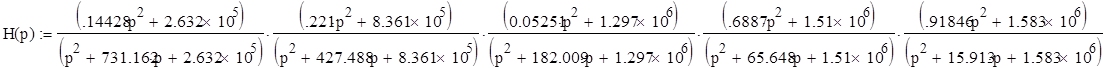
При этом АЧХ фильтра такова:
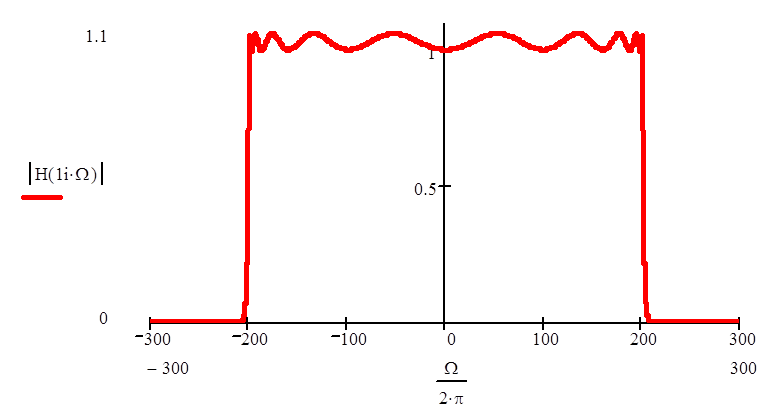 |
Для того чтобы посмотреть на колебания в зоне подавления сигнала немножко увеличим масштаб:
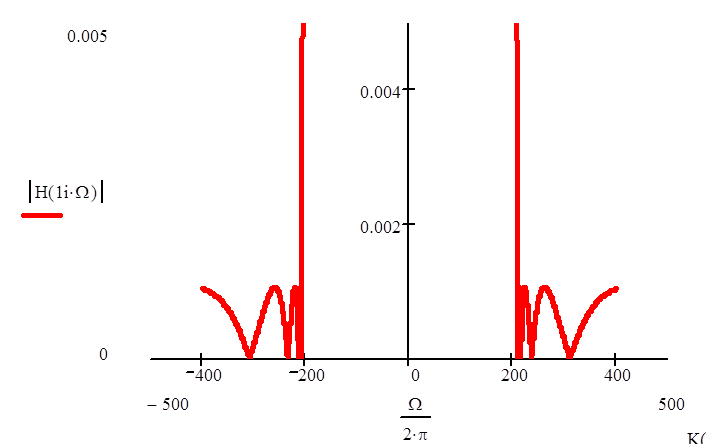 |
В итоге получили характеристику эллиптического фильтра.
Теперь проверим соответствие полученных характеристик теми, что даны в техническом задании. Для этого постоим график, позволяющий оценить пульсации в полосе пропускания и задерживания.
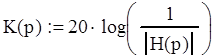
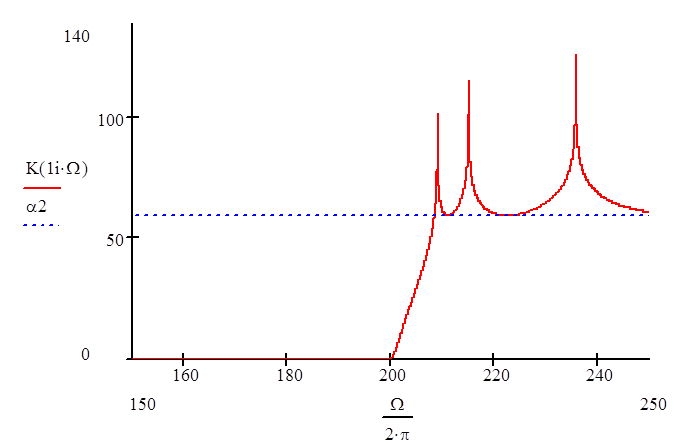 |
Как видно из графика, пульсации в полосе задерживания не менее 60 дБ.
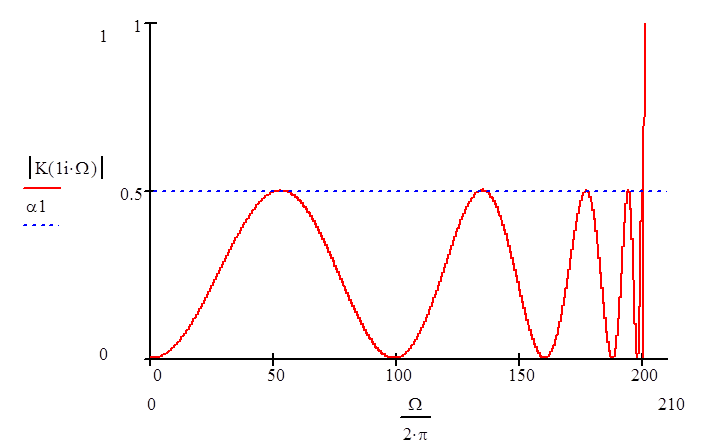 |
Пульсации в полосе задерживания практически не более 0.5 дБ, что тоже соответствует техническому заданию.
Воспользуемся билинейным преобразованием.
Сделаем следующую подстановку в передаточную функцию:
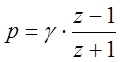
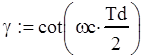 |
|||
Отсюда получаем что:

или, что то же самое

Коэффициенты в маткаде получаются длинные, поэтому их немного округлил. Причем, чтобы не потерять значимость округление производилось так:
Сначала построил график W(z), а потом начинал удалять по одной цифре. Если вид графика заметно не менялся, то удалял еще одну цифру, а если изменялся, то возвращал цифру назад и переходил к следующему коэффициенту.
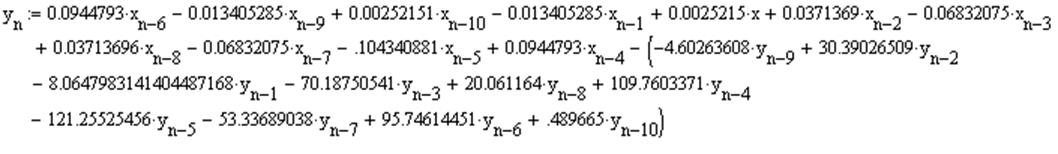
После
этого легко получаем разностное уравнение:
5.Оценка соответствия фильтра техническому заданию
Построим на графике АЧХ цифрового фильтра, а затем оценим, насколько изменились его характеристики по сравнению с аналоговым (частота среза, пульсации в зоне пропускания и задерживания)
АЧХ
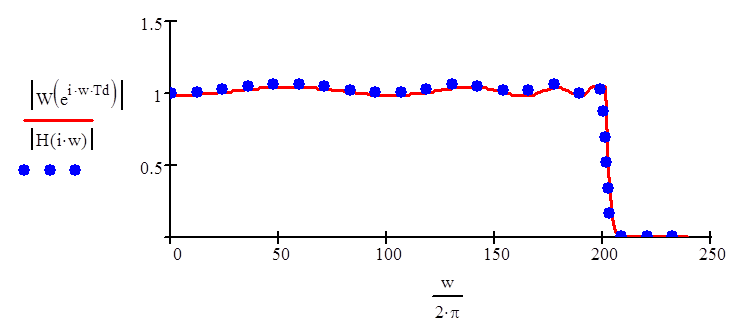 |
Частота среза цифрового фильтра получилась равна 200 Гц, как и требуется в техническом задании. Наклон характеристики получился более крутым, так как порядок взят несколько выше, чем получалось из монограммы (10, а не 9.4) и из-за свойств билинейного преобразования. Но это как раз и есть положительное качество эллиптического фильтра: при не очень больших порядках характеристика получается довольно крутая.
Проверим пульсации в полосе задерживания и сравним их с полученными в аналоговом фильтре:
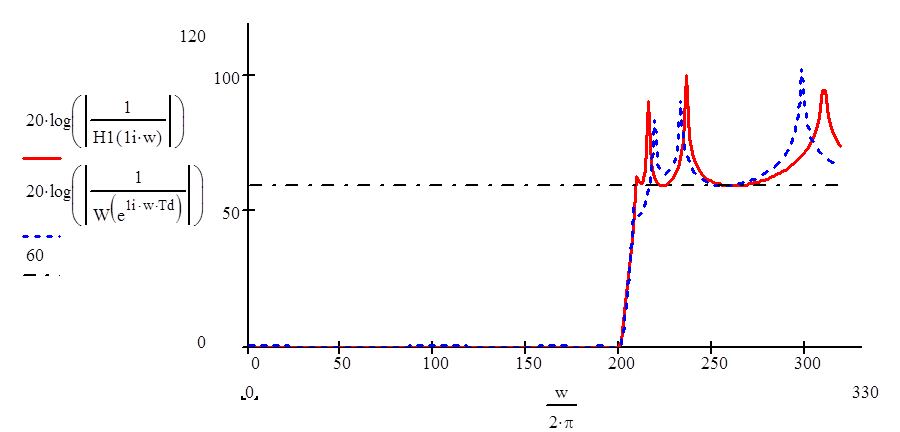 |
Как видно из графика, пульсации в полосе задерживания, начинающейся с 230Гц, более 60 дБ, что соответствует техническому заданию.
Проверим пульсации в полосе пропускания и сравним их с полученными в аналоговом фильтре:
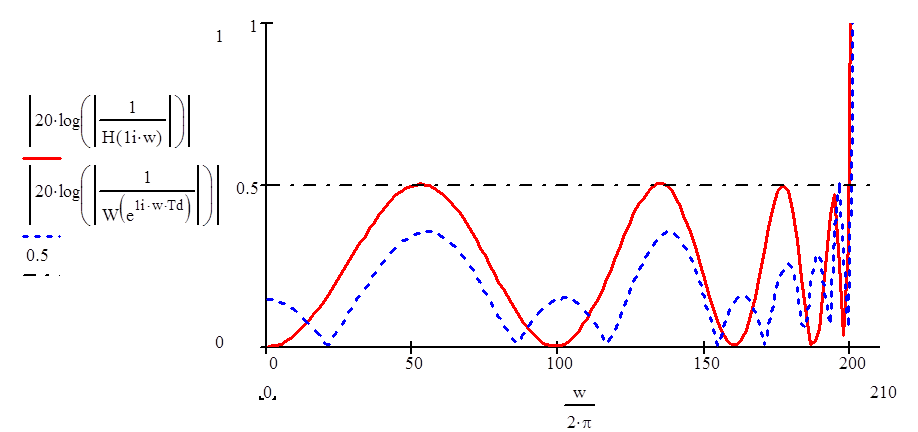 |
Зададим сигнал с частотой 100Гц (полоса пропускания) и наложим на него помеху частотой 300Гц (частота задерживания). Пусть помеха и сигнал равны по амплитуде.
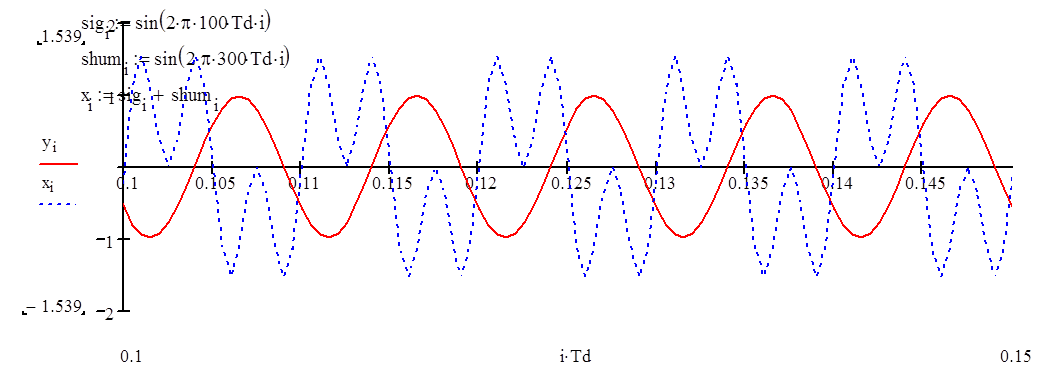
Х – это сигнал, подаваемый на фильтр (полезный сигнал + помеха)
У – это сигнал на выходе фильтра
Если сравнить исходный сигнал и сигнал после фильтра, то получим:
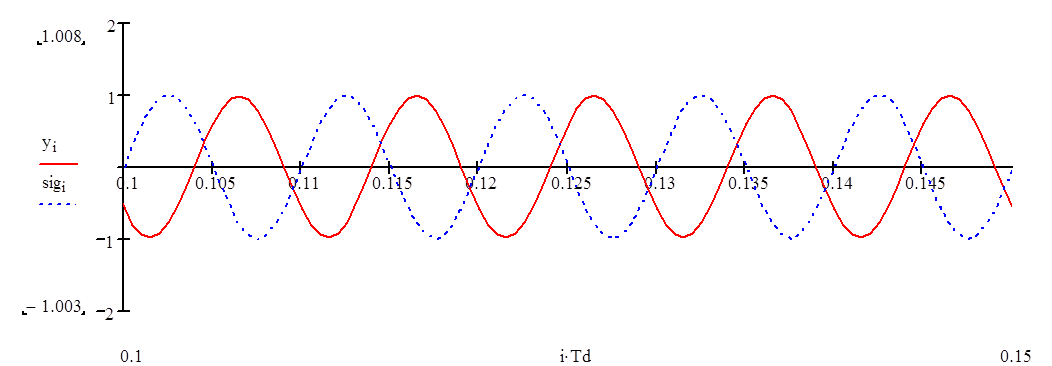 |
Как видно, фильтр немножко сдвигает сигнал, то есть задерживает.
Рассчитаем значения максимального ослабления в полосе пропускания и минимального ослабления в полосе задерживания:
Полезный сигнал на входе фильтра имеет амплитуду 1, на выходе 0.979
Ослабление рассчитывается как:
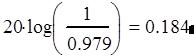 |
Помеха на входе фильтра имеет амплитуду 1, на выходе 0.00037
Ослабление рассчитывается как:
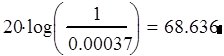 |
В итоге получили малое ослабление полезного сигнала и значительное ослабление помехи. Величины ослабления соответствуют техническому заданию.
В ходе данной работы был выполнен расчет цифрового эллиптического фильтра или фильтра Кауэра. Полученный фильтр соответствует требованиям технического задания, причем переходная полоса получилось очень узкой. Это характеризует фильтр с лучшей стороны, так как основной плюс эллиптического фильтра – это узость его переходной зоны при не очень большом порядке фильтра.
Также с помощью данного фильтра проведена фильтрация тестового сигнала. Сигнал на выходе фильтра совпадает по форме с гармоникой тестового сигнала, частота которой лежит в полосе пропускания фильтра. При этом максимальное ослабление в полосе пропускания и минимальное ослабление в полосе задерживания соответствуют требованиям.
1. Д. Джонсон, Дж. Джонсон Справочник по активным фильтрам. М.: Энергоатомиздат 1983.
2. Голышев Н.В., Щетинин Ю.И. "Теория и обработка сигналов" часть 2, учебное пособие. Новосибирск: НГТУ 1998.
3. Лем Г. "Аналоговые и цифровые фильтры: расчёт и реализация". М.: "Мир" 1982.
4. Зааль Р. Справочник по расчету фильтров. М.: Радио и связь 1983.
5. Голованов В.В. "Проектирование аналоговых и цифровых фильтров". М.: 1983.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.