Проектирование цифрового полосового БИХ-фильтра Баттерворта. Вариант 6, страница 4

Аппаратная реализация цифровых фильтров основана на использовании той или иной формы уравнения или передаточной функции.

Для прямой формы реализации уравнение ЦФ:

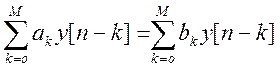
Первая его часть не имеет полюсов передаточной характеристики, ее выход подключается ко входу второй части, передаточная характеристика которой обладает только полюсами и не имеет нулей. Передаточная характеристика всего фильтра воспроизводит выражение уравнения фильтра, то есть обладает как нулями, так и полюсами.

            Для такой формы реализации характерно избыточное по сравнению с другими формами количество элементов и ярко выраженная чувствительность характеристик фильтра к погрешностям коэффициентов.

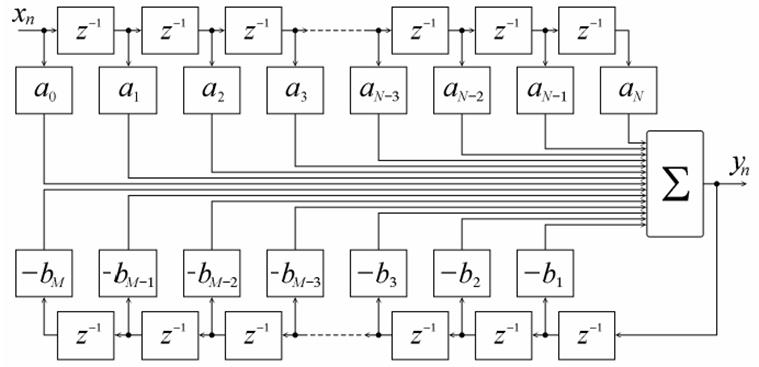
Рис. 7. Первая прямая форма построения цифровых фильтров.

Структурная схема, приведенная на рис. 7, называется первой прямой формой построения цифрового фильтра. Альтернативой первой прямой формы является вторая прямая форма, которая получается из структурной схемы рис. 7 перестановкой частей – первая часть фильтра имеет передаточную характеристику без нулей, а вторая – без полюсов.

Получающаяся при этом структурная схема фильтра приведена на рис. 8. Главным ее достоинством, как это видно из рисунка, является уменьшенное по сравнению с первой прямой формой количество элементов задержки. Действительно, первая прямая форма использует M + N элементов задержки, а вторая – min(N,M). Частным случаем этой формы является так называемая биквадратная форма. Знаменатель такой формы представляет многочлен второго порядка, имеющий два действительных корня или комплексно-сопряженные корни [5].

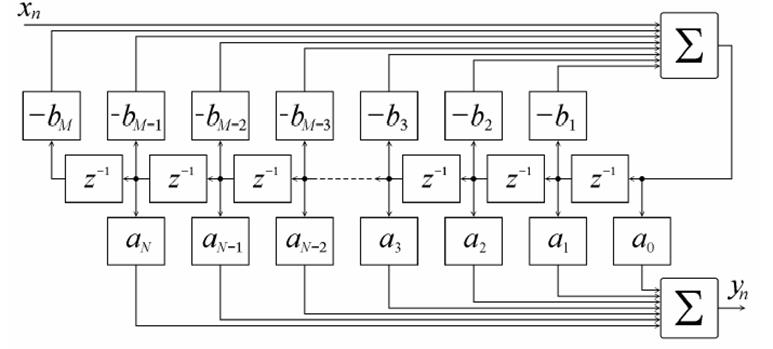
Рис. 8. Вторая прямая форма (каноническая форма) построения цифровых фильтров.

Числитель и знаменатель функции передачи физически реализуемого дискретного фильтра можно разложить на линейные (относительно z^-1) множители. Перемножение функций передачи соответствует последовательному (каскадному включению) соответствующих фильтров, поэтому такое представление дает реализацию фильтра в виде последовательно включенных фильтров 1-го порядка (при этом некоторые из них могут иметь комплексные коэффициенты) либо фильтров 1-го и 2-го порядка с вещественными коэффициентами [4].

Для последовательной формы реализации цифровых фильтров характерно меньшая чувствительность к погрешностям квантования. Передаточная функция цифровых фильтров:

                   

         

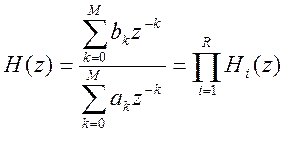
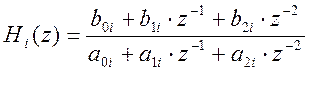
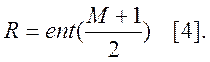
Рис. 9. Структурная схема последовательной формы.

            Еще один способ преобразования функции передачи физически реализуемого фильтра – представление ее в виде суммы простейших дробей. Каждое из слагаемых при таком представлении соответствует функции передачи рекурсивного фильтра 1-го порядка (возможно, с комплексными коэффициентами) либо 1-го либо 2-го порядка (если используется представление виде суммы простейших дробей только с вещественными коэффициентами). Сама операция сложения эквивалентна параллельному соединению этих фильтров с суммированием выходных результатов [4].

Для параллельной формы реализации:

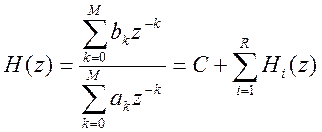
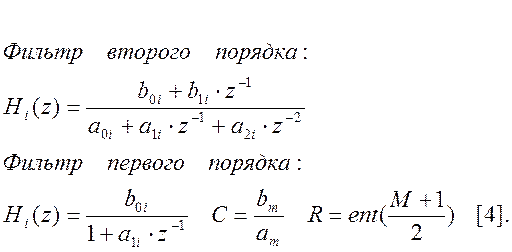
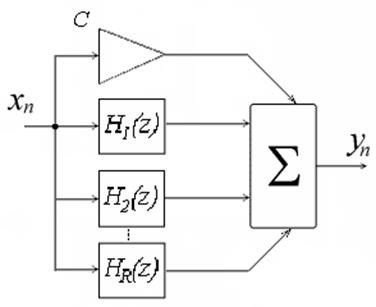
Рис. 10. Структурная схема параллельной формы.

Для реализации спроектированного мною фильтра была использована последовательная форма реализации, так как она позволяет избежать «лишних» погрешностей квантования. Для этого были использованы следующие функции Matlab:

[z,p,k]=tf2zp(numd, dend);

sos=zp2sos (z,p,k)

sos =                     0.00049884915809   0.00099977100790   0.00049925711084

  1.00000000000000  -0.79446737220084   0.22454232410498

   1.00000000000000   2.08152676874561   1.08503305806535

   1.00000000000000  -0.57757068107997   0.28376684681097

   1.00000000000000   1.99585609914310   0.99918417173376

   1.00000000000000  -1.26980348294070   0.43814108500755

   1.00000000000000   1.91846218533915   0.92162971461078

   1.00000000000000  -0.49030029957593   0.46702055865577

   1.00000000000000  -2.05934868034802   1.06038646752032

   1.00000000000000  -1.52185441077850   0.63192681571954

   1.00000000000000  -2.02338380364563   1.02440115075632

   1.00000000000000  -0.49762477042068   0.77772516257355

   1.00000000000000  -1.94234922732428   0.94331682097064

   1.00000000000000  -1.68986092799044   0.78199071968256

   1.00000000000000  -1.97491828868100   0.97590644672408

   1.00000000000000  -1.83632097835579   0.92484763942323

        

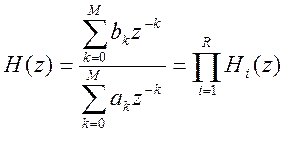
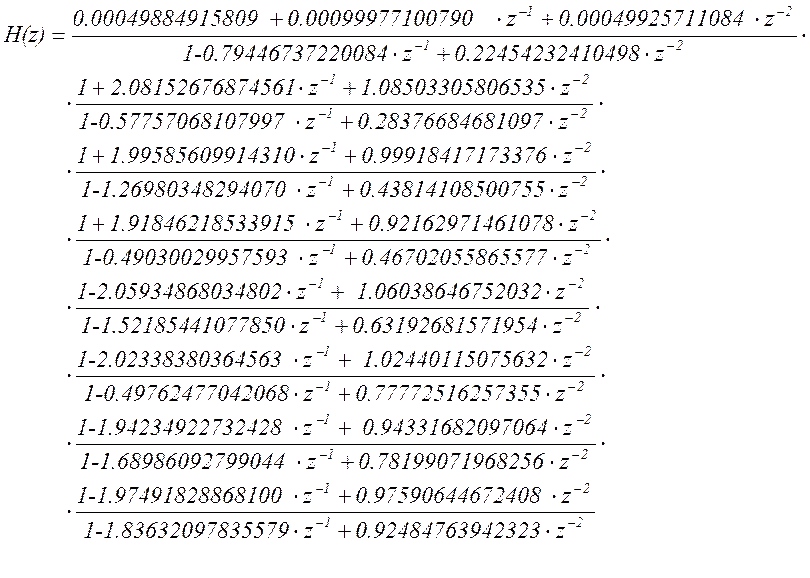
Рис. 11. Структурная схема реализации цифрового полосового БИХ-фильтра Баттерворта.

Графики АЧХ исходного фильтра и АЧХ каскадного фильтра изображены на рис. 12 , построенные с помощью следующих команд:

[z, p, k]=sos2zp(sos);

[b_q, a_q]=zp2tf(z, p, k);

[H_q, f1]=freqz(b_q, a_q, 256, Ft);

figure(6)

plot(f, abs(H), f1,abs(H_q), '--'),set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

grid on

axis([0,12000,0,1.1])

legend('Амплитудный спектр проектируемого фильтра', 'Амплитудный спектр каскадного фильтра')

xlabel('Частота, Гц')

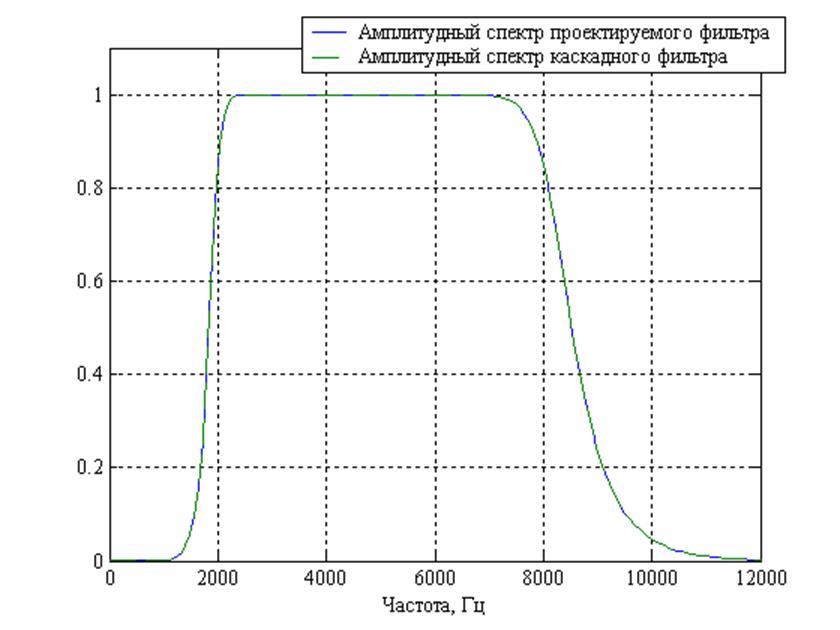
Рис. 12. АЧХ исходного и каскадного фильтров.

Реализация спроектированного фильтра была осуществлена без округления коэффициентов каскадной формы, что обосновывается большой чувствительностью коэффициентов к округлению. Как видно из графиков представленных на рис. 15, что АЧХ исходного и каскадного фильтров совпадают.

Тестирование  фильтра