Проектирование цифрового полосового БИХ-фильтра Баттерворта. Вариант 6, страница 6

double  duration;                            // переменная, в которую запишем время обработки

int i;

for( i=0;i<N;i++)

x[i]=sin(N*2*3.14159*Td*i);         // получаем текущий элемент массива х

printf("Numbers of count N=5000\n");

start = clock();                                  // запоминаем время начала обработки

                for(i=16;i<N;i++)

                        {

                                        for(int k=0;k<=16;k++)

                                                    {

                                                            y[i]+=b[k]*x[i-k];

                                                }

                                        for(int k=0;k<=16;k++)

                                                {

                                                            y[i]-=a[k]*y[i-k];

                                                }

                        }

finish = clock();                               // время завершения

duration = (double)(finish - start) / CLOCKS_PER_SEC; // записываем в переменную время обработки

printf( "Filtering Time=%2.5f seconds\n", duration ); // вывод времени обработки

printf( "Done!\n" );

sleep( (clock_t)4 * CLOCKS_PER_SEC );

};

Будем оценивать время обработки одного отсчета (Т) в режиме реального времени с выводом времени выполнения на экран. А так же определим максимальную частоту (f_max), которую способен обрабатывать цифровой фильтр на базе данного компьютера. Она будет обратно пропорциональна времени обработки одного отсчета, так как если подавать сигнал чаще, чем происходит обработка,  то в режиме реального времени данная система не будет успевать за входным сигналом.

Рис.18.  Работа программы: при N=2000 отсчетов время фильтрации сигнала=16 мсек

Рис.19.  Работа программы: при N=5000 отсчетов время фильтрации сигнала=31 мсек

Рис.20.  Работа программы: при N=10000 отсчетов время фильтрации сигнала=47 мсек

Рис.21.  Работа программы: при N=20000 отсчетов время фильтрации сигнала=62 мсек

Рис.22.  Работа программы: при N=50000 отсчетов время фильтрации сигнала=63 мсек

При запуске программы на компьютере с процессором Intel Pentium D 3.06 ГГц мы получаем следующие результаты:

Количество отсчетов (N)	Общее время (t), сек.	Время обработки одного отсчета (Т), мкс	Максимальная частота (fmax), кГц
2000	0,016	8	125
5000	0,031	6,2	161,3
10000	0,047	4,7	125
20000	0,062	3,1	322
50000	0,063	1,26	793,65

Табл. 2. Результаты выполнения программы.

Т = время обработки всех отсчетов/количество отсчетов

Т = t/N;

f_max =1/T;

Для реальной работы данного фильтра на данной системе надо подавать сигналы, так что бы они в любом случае обрабатывались, а это значит, что для оценки общей f_max надо из всех экспериментов выбрать наихудший: f_max = 125 КГц – максимальная обрабатываемая частота цифровым фильтров.

* для более точного определения f_max стоило бы провезти тестирование большее  количество раз.

Заключение

В ходе данной работы был спроектирован цифровой полосовой БИХ-фильтр Баттерворта, со следующими характеристиками:

§  Нижняя частота среза  - 2 кГц,

§  Верхняя частота среза  - 8 кГц

§  Нижняя граничная частота  полосы задерживания– 1,247  кГц,

§  Верхняя граничная частота полосы задерживания – 11  кГц,

§  Минимальное ослабление в полосе задерживания – 40 дБ,

§  Минимальное ослабление в полосе пропускания – 2 дБ,

§  Частота дискретизации – 40 кГц.

В качестве метода проектирования был выбран метод билинейного преобразования, относящийся к методам с использованием аналогового прототипа. Он был использован в проектировании в виду его простоты и качеств результирующих фильтров.

В результате проделанной работы удалось разработать фильтр с дос­таточно хорошей амплитудно-частотной характеристикой, у которой практически нет отклонения АЧХ от 0 в полосе пропускания, неравномерность в полосах задерживания удовлетворяет заданной. Такой результат был достигнут из-за того, что порядок фильтра достаточно высок. Поэтому ФЧХ далека от иде­альной, она нелинейная.

Для получения полосового фильтра с лучшей АЧХ необходимо нижнюю и верхнюю граничные частоты  задерживания взять равными 1,2 кГц и 8,8 кГц соответственно, частоту дискретизации равной 20 кГц. Остальные характеристики оставить неизменными.  При этом  порядок фильтра останется равным 16, а полученный фильтр будет иметь АЧХ более близкую к АЧХ идеального фильтра.

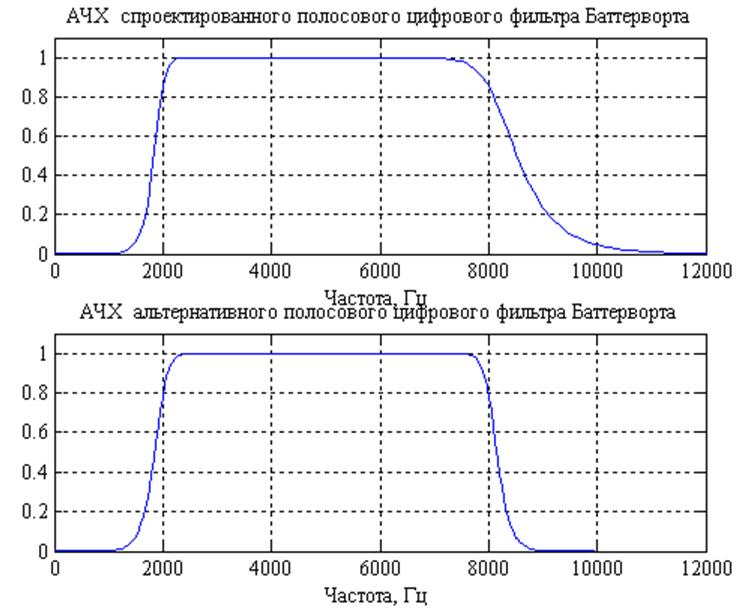
Рис.23. Графики АЧХ спроектированного и альтернативного ПФ Баттерворта.

Тестирование, приведенное в этой работе показало, что спроектированный фильтр удовлетворяет условиям определенным в задании. Фильтр пропускает сигналы с частотами в пределах от 2000 до 8000 Гц, и подавляет гармоники с частотами, выходящими за эти пределы.

Список литературы

1.  Голышев Н.В., Щетинин Ю.И. Задачник – практикум по теории и обработке сигналов: Учеб. пособие. – Новосибирск. Изд-во НГТУ,  2001. – Ч.2. – 80  с.

2.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов: Учеб. пособие. – Новосибирск. Изд-во НГТУ, 1998. – Ч.2. – 115  с.

3.  http://matlab.exponenta.ru/index.php

4.  Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 608 с.: ил.

5.  Белодедов М.В.Методы проектирования цифровых фильтров: Учебное пособие.

Волгоград: Изд-во Волгоградского государственного университета, 2004. – 64 с.

dsp-book.narod.ru/methodNF.pdf