Информатика и выч. техника \ Теория и обработка сигналов

Проектирование цифрового полосового БИХ-фильтра Баттерворта. Вариант 6, страница 2

Вторую группу методов расчета рекурсивных фильтров составляют так называемые прямые методы расчета в z-плоскости, основанные на выборе полюсов и нулей фильтра, обеспечивающих необходимый вид его амплитудной характеристики.

Наконец, к третьей группе методов расчета БИХ-фильтров относятся так называемые методы оптимизации, обеспечивающие минимум ошибки между аппроксимирующей и заданной характеристиками фильтра. [2].

В данной работе использовался метод, относящийся к методам, основанных на использовании аналоговых прототипов, а именно: метод билинейного преобразования. Этот метод применяется наиболее часто ввиду его простоты и ка­честв результирующих характеристик фильтров.  Достоинством метода билинейного преобразования является то, что передаточная функ­ция цифрового фильтра определяется с помощью простых формул из передаточной функ­ции аналогового фильтра, для которых существуют подробные таблицы и справочники. Еще одним достоинством этого метода по сравнению с другими методами преобразования аналоговых фильтров в цифровые (инвариантности импульсной характе­ристики и согласованного z-преобразования) выделяют то, что данный метод обеспечивает построение  такого БИХ-фильтра, выходной сигнал которого приближенно совпадает с выходным сигналом аналогового фильтра-прототипа при одинаковых произвольных вход­ных сигналах.

Метод билинейного преобразования основан на использовании конформного преобразования р-плоскости с помощью функции 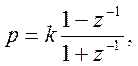                           (1)

где – положительная константа.

            При переходе от ПФ аналогового фильтра к ПФ цифрового фильтра используется следующее выражение:

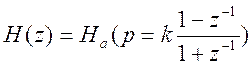
Соответствие между частотами аналогового фильтра W и w цифрового фильтра следует из подстановки в выражение (1) и, где  – интервал дискретизации. При такой подстановке: 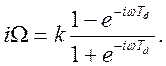 Эквивалентное выражение 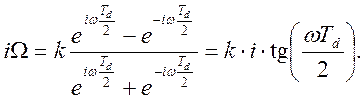 Отсюда  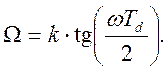Преобразование     является нелинейным, но оно близко к линейному при небольших w. Частота среза   аналогового прототипа соответ­ствует частоте среза  цифрового фильтра. По значениям  и  можно вычис­лить постоянную .

Если аналоговый фильтр нормализован и то 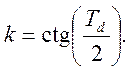 При этом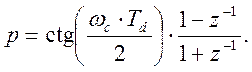

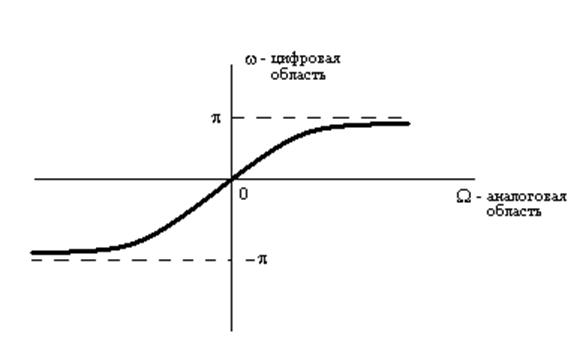
Рис. 2. Связь между частотами аналоговой и цифровой областей.

Как видно из рис. 2. связь между частотами аналоговой и цифровой областей – нелинейная. Чтобы использовать билинейное преобразование, необходимо исходные частоты цифрового фильтра преобразовать в частоты аналогового фильтра – деформация частот, преобразование в частотной области.

Рассмотренное билинейное преобразование (1) позволяет получить передаточную функ­цию цифрового фильтра из передаточной функции аналогового фильтра [1].


Проектирование фильтра

Итак, как было сказано выше, проектирование целевого фильтра будет осуществляться методом билинейного преобразования. Данный метод проектирования можно разбить на три этапа:

1. Получение спецификации аналогового фильтра на основе спецификации цифрового фильтра.

2.  Проектирование аналогового фильтра (прототипа).

3.  Трансформация аналогового фильтра в цифровой.

Проектирование требуемого цифрового фильтра осуществляется в среде MatLab 6.5 фирмы The MathWorks, Inc.

  1. Получение спецификации АФ на основе спецификации ЦФ

Для начала нужно задать характеристики идеального полосового фильтра (ПФ) с требуемыми в задании характеристиками, который мы, собственно, и будем использовать для получения нужного нам цифрового полосового БИХ-фильтра Баттерворта.

Спецификация цифрового фильтра:

Fs1=1200;   %Гц

Fp1=2000;   %Гц

Fp2=8000;   %Гц

Fs2=11000; %Гц

Ft=40000;   %Гц

Rs=40;       %Дб

Rp=3;        %Дб

Определение нормированных частот:

ws1 = 2*pi*Fs1./Ft  %  [pад/с]/отсч

wp1 = 2*pi*Fp1./Ft  %  [рад/с]/отсч

wp2 = 2*pi*Fp2./Ft  %  [рад/с]/отсч

ws2 = 2*pi*Fs2./Ft  %  [рад/с]/отсч

ws1 =   0.18849555921539

wp1 =   0.31415926535898

wp2 =   1.25663706143592

ws2 =   1.72787595947439

Дальнейшее проектирование заключается в вычисление граничных частот аналогового фильтра:

Ws1 = 2*Ft*tan(ws1/2)

Wp1 = 2*Ft*tan(wp1/2)

Wp2 = 2*Ft*tan(wp2/2)

Ws2 = 2*Ft*tan(ws2/2)

Ws1 =    7562.226494342564

Wp1 =    12670.75522596290

Wp2 =    58123.40224042886

Ws2 =    93667.96528900311

Проверка условия геометрической симметрии:

SimWs = Ws1*Ws2=    7.083383687796589e+008

SimWp =Wp1*Wp2=   7.364674026886579e+008

Как видно, что условие геометрической симметрии не выполняется, и, значит, возникает необходимость корректировать граничные частоты в полосе задерживания:

W_s1=Wp1*Wp2./Ws2

F_s1=(Ft*(2*atan(W_s1/2/Ft)))/2/pi

Ws1=W_s1

if(Ws1*Ws2==Wp1*Wp2)

    msgbox('Условие геометрической симметрии выполняется!','Внимание!');

end

В результате корректировки нижней частоты задерживания получаем:

W_s1 =    7.862532301372850e+003

 F_s1  =    1.247354988752664e+003

При корректировке нижней частоты задерживания получаем наилучший результат (Fs1=1247 Гц), так как улучшается вид АЧХ. При корректировке верхней частоты задерживания получили бы F_s2=1.124406275304836e+004, что делает получаемую АЧХ более отдаленной от АЧХ идеального фильтра.

Ширина полосы пропускания:

BW = Wp2-Wp1

BW = 4.545264701446596e+004

Центральная частота полосы пропускания:

W0 = sqrt (Wp1*Wp2)

W0 = 2.713793291112383e+004

2. Проектирование аналогового прототипа

Расчет нормированного ФНЧ:

Определение граничной частоты полосы задерживания:

Omega_s = (Ws2-Ws1)/(Wp2-Wp1))

Omega_s = 1.88779837091383

Скачать файл