Проектирование цифрового полосового БИХ-фильтра Баттерворта. Вариант 6, страница 3

Нахождение порядка НФНЧ: выбрать минимальный порядок фильтра позволяет функция buttord(). Данная функция позволяет выбирать порядок как для дискретных, так и для аналоговых фильтров. Признаком дискретного расчета является отсутствие  строки ‘s’ в конце списка входных параметров. Входной параметр Rp –допустимый уровень пульсаций в полосе пропускания (в децибелах), Rs – минимально необходимое затухание в полосе задерживания (в децибелах) [4].

[n, Wn] = buttord(1, Omega_s, Rp, Rs, 's'))

            n =  8

Wn = 1.06159367286336

Порядок фильтра равен 8, частота среза фильтра – 1.06159367286336

Определение передаточной функции НФНЧ выполняется с помощью функции MatLab butter(). Входной параметр n – порядок фильтра, Wn – частота среза, ‘s’ – строка, указывающая на то, что производится расчет аналогового фильтра [3], [4].

[num, den] = butter(n, Wn, 's');

Преобразование НФНЧ в ПФ производится с помощью функции lp2bp. Входными параметрами функции являются описание фильтра (в виде коэффициентов полиномов числителя и знаменателя функции передачи – num, den), средняя частота W0  и ширина BW полосы пропускания фильтра (в радианах в секунду) [4].

[BT, AT] = lp2bp(num, den, W0, BW);

При этом преобразовании порядок фильтра увеличивается вдвое, таким образом, порядок аналогового прототипа равен 16.

Таким образом, характеристики полученного аналогового фильтра таковы:

Характеристики	Ws1	Wp1	Wp2	Ws2	Rs	Rp	Ft
Желаемые	1200 Гц	2000 Гц	8000 Гц	11000 Гц	40 дБ	3 дБ	40000 Гц
Полученные	1247 Гц	2000 Гц	8000 Гц	11000 Гц	40 дБ	3 дБ	40000 Гц

Таблица 1. Желаемые и полученные характеристики аналогового фильтра.

3. Преобразование аналогового прототипа в ЦФ

Для преобразования аналогового прототипа в ЦФ используется функция bilinear(), где ВТ, АТ – коэффициенты полиномов числителя и знаменателя функции передачи  аналогового прототипа. Параметр  Ft задает частоту дискретизации в герцах [4].

[numd, dend] = bilinear(BT, AT, Ft)

numd =

  0.00049884915809         0.00000000000001          -0.00399079326485

  0.00000000000040       0.01396777642546               0.00000000000205

-0.027935552855810         0.00000000000307            0.03491944106372

  0.00000000000190       -0.02793555285419                          0.00000000000046

  0.01396777642641            0.00000000000005          -0.00399079326474

  0.00000000000000       0.00049884915809

dend =

  1.000000000000           -8.677802923343                   36.377624181453

-98.198275640578                          191.631314325146               -287.108772148849

  341.728963363368         -329.485746185612                259.925095008817

-168.242894288576           89.022621415581                  -38.096391080543

  12.927857754314             -3.364906624499                    0.634202105561

-0.077466072584              0.004634197868

4. Уравнение фильтра

Передаточная функция полосового фильтра имеет вид дробно-рационального выражения:

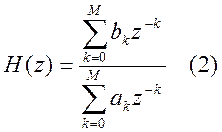
В общем виде линейный цифровой фильтр описывается линейным разностным уравнением с постоянными коэффициентами:

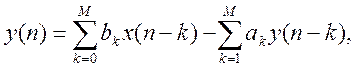
где x(n) – входной сигнал, y(n) – выходной сигнал, a_k, b_k – коэффициенты фильтра.

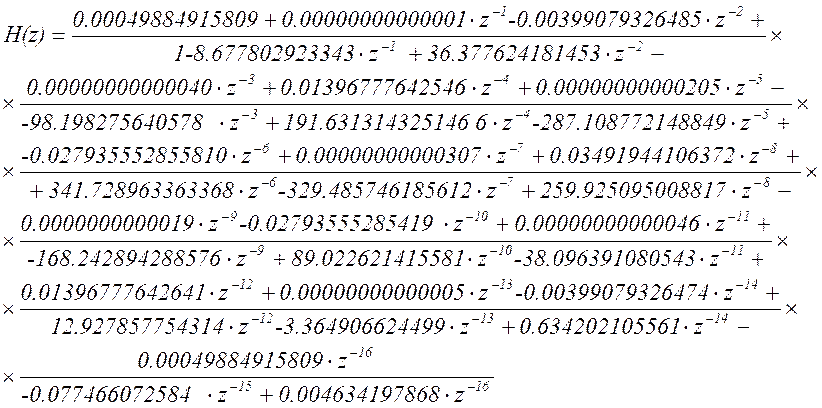
Откуда уравнение фильтра будет иметь следующий вид:

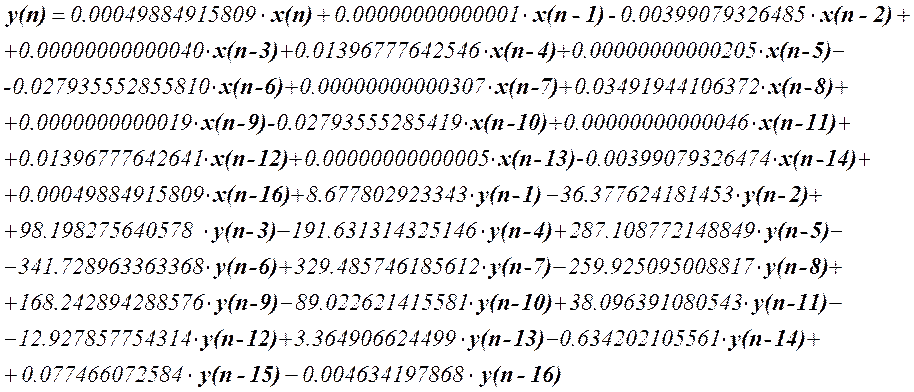
Диаграмма нулей и полюсов:

figure(1)

zplane(numd, dend);

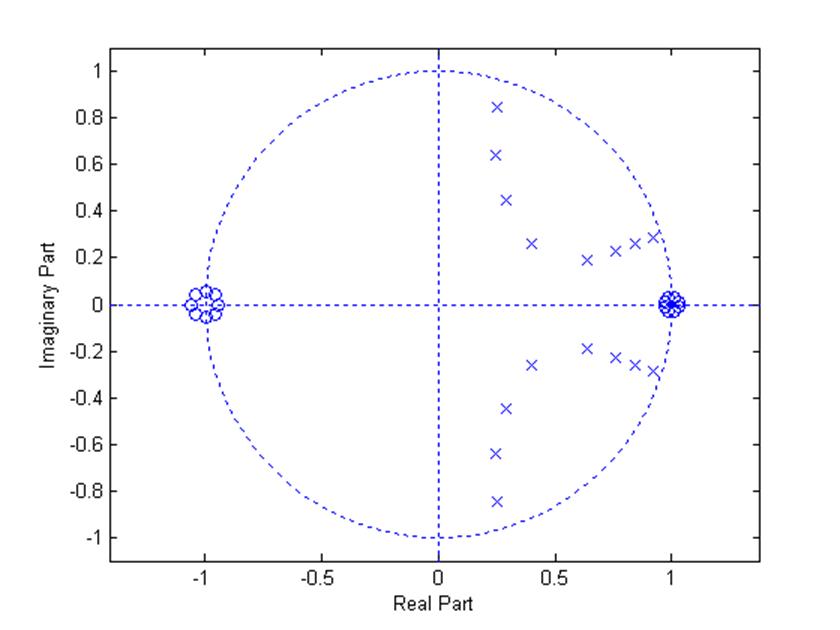
Рис. 3. Диаграмма нулей и полюсов.

По условию устойчивости полюсы должны быть внутри единичного круга на плоскости z. Из полученной диаграммы видно, что спроектированный фильтр устойчив, так как все его полюса строго лежат внутри круга единичного радиуса.

Построение АЧХ и ЛАЧХ цифрового полосового фильтра Баттерворта:

figure(2)

subplot(211)

plot(f, abs(H),'LineWidth',2),

set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

grid on

title('АЧХ полосового цифрового фильтра')

xlabel('Частота, Гц ')

subplot(212)

plot(f, 20*log10(abs(H)),'LineWidth',2),set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

grid

title('ЛАЧХ полосового цифрового фильтра')

xlabel('Частота, Гц ')

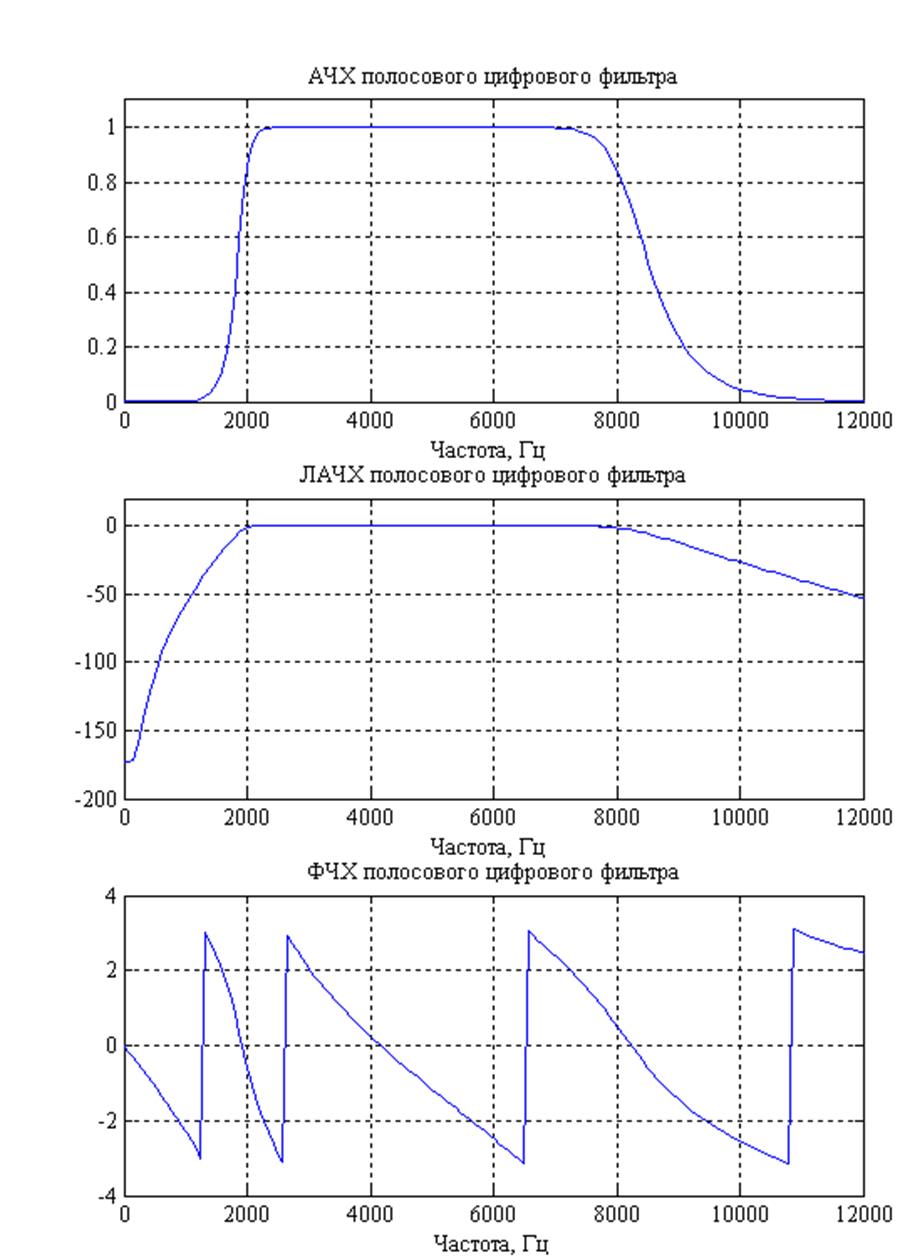
Рис. 4. Графики АЧХ, ЛАЧХ и ФЧХ  цифрового ПФ Баттерворта.

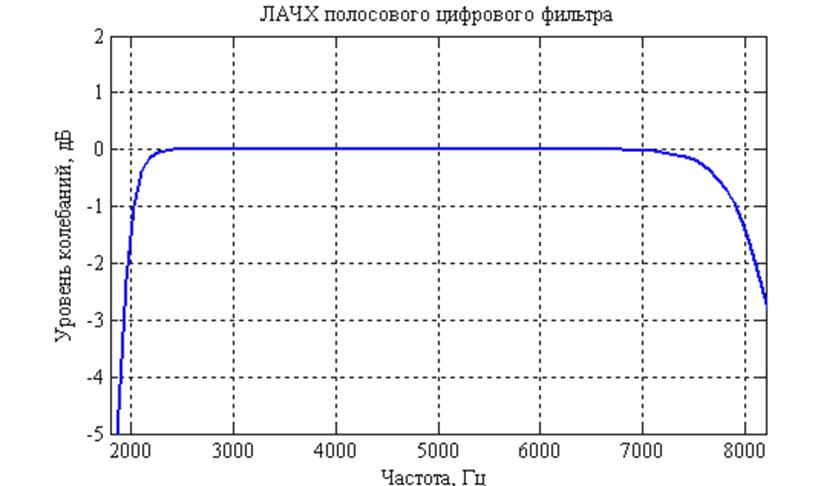
Рис. 5. Полоса пропускания фильтра (увеличенный масштаб).

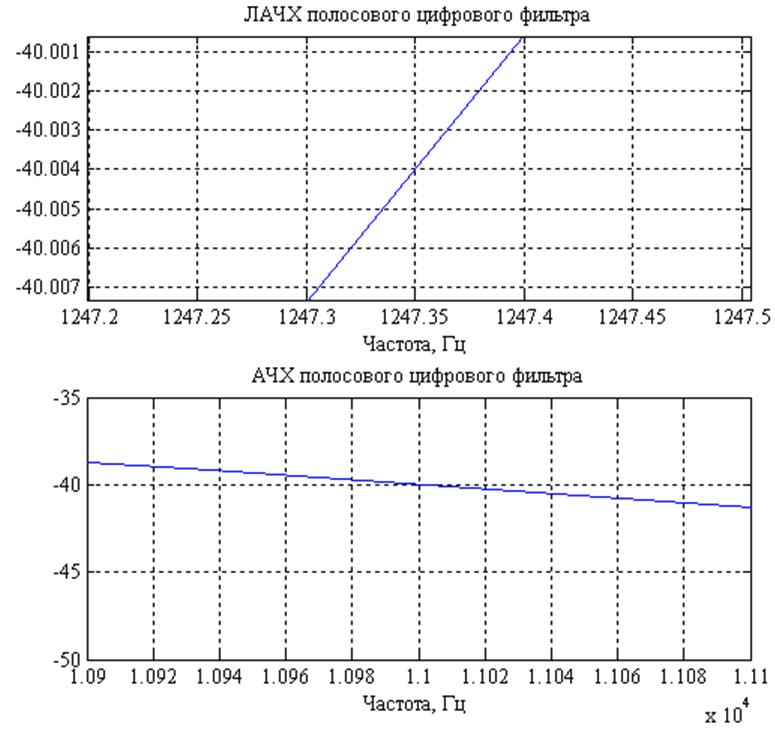
Рис. 6. Увеличенный масштаб нижней и верхней граничных частот полосы задерживания соответственно.

Из рис. 5. видно, что неравномерность в полосе пропускания составляет около 2 дБ. Графики ЛАЧХ  на рис. 6 показывают, что ослабление в полосе задерживания полностью соответствует требуемой спецификации, т.е. ослабление в полосе задерживания составляет не менее 40 дБ: при нижней граничной частоте полосы задерживания эта величина составляет -45.004 Дб, при верхней частоте полосы задерживания – -40 Дб (эти значения были получены с использованием функции MatLab zoomon).

Реализация фильтра

Реализация цифровых фильтров может быть самой разной, причем совершенно различные на первый взгляд фильтры могут обладать идентичными передаточными характеристиками. Цифровой фильтр с заданной передаточной характеристикой можно реализовать различными способами. Это дает разработчику лишнюю «степень свободы», позволяя помимо заданной передаточной характеристики добиться выполнения каких-либо других требований, таких как минимизация шумов дискретизации по уровню, минимизации числа элементов схемы фильтра и т.д.