Информатика и выч. техника \ Теория и обработка сигналов

Проектирование цифрового полосового БИХ-фильтра Баттерворта. Вариант 6, страница 5

В задачах обработки сигналов основное применение фильтров заключается в выделении полезного сигнала из аддитивной смеси его с шумом. Пусть входной сигнал представляет собой сумму дискретных гармоник с частотами 1500 Гц (шум) и 6000 Гц (полезный сигнал). Первая гармоника входит в полосу задерживания фильтра, вторая - в полосу пропускания. Из рис. 13 следует, что выходной сигнал фильтра воспроизводит только вторую гармонику и подавляет первую.

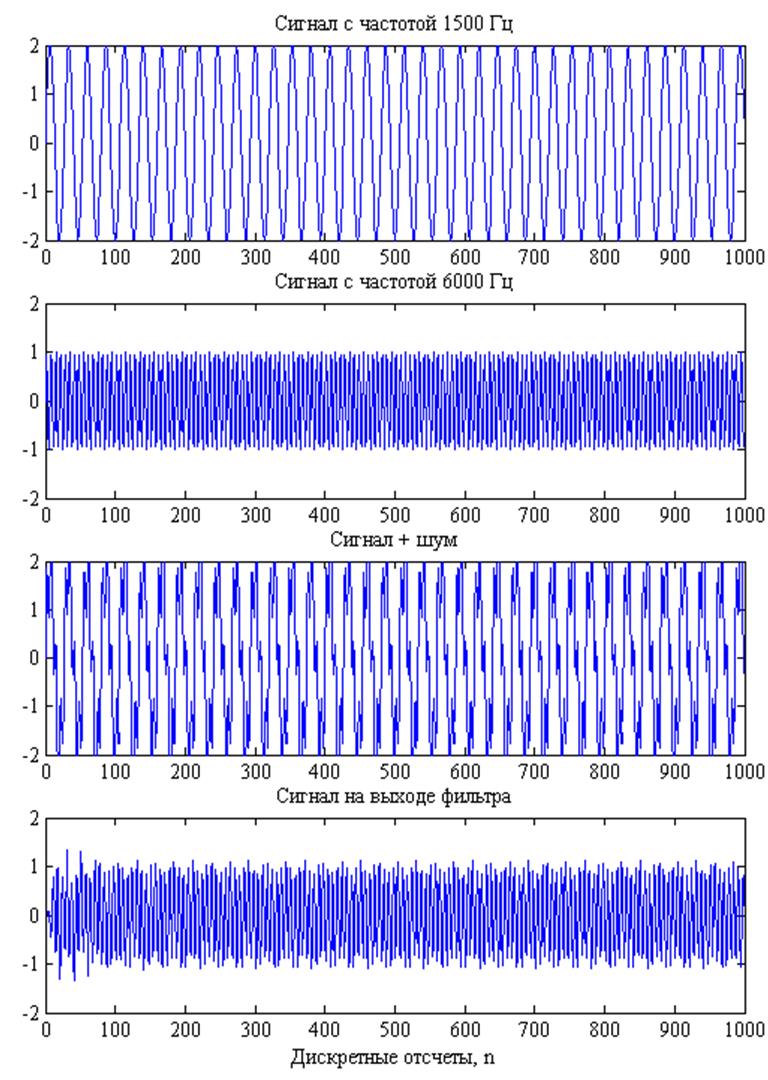
Рис. 13. Сигналы с частотами 1500 и 6000 Гц, суммарный сигнал и сигнал на выходе фильтра.

Код, с помощью которого получены результаты на рис. 13:

N=1000;

i=0:1:N-1;

Tt=1./Ft;

s=2*sin(2*pi*1500*Tt*i);

s1=sin(2*pi*6000*Tt*i);

x=s+s1;

subplot(411)

plot (i, s), axis([0,1000,-2,2]),

set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал с частотой 1500 Гц' )

subplot(412)

plot (i, s1), axis([0,1000,-2,2]),

set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал с частотой 6000 Гц')

subplot(413)

plot (i, x), axis([0,1000,-2,2]),

set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал + шум')

subplot(414)

F=filter(numd, dend, x);

plot(i, F),  axis([0,1000,-2,2]),

set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал на выходе фильтра')

xlabel('Дискретные отсчеты, n')

Пронаблюдаем, каким будет сигнал после фильтрации при подаче сигналов

с частотами  2000 и 8000 Гц:

N=1000;

i=0:1:N-1;

Tt=1./Ft;

s=sin(2*pi*2000*Tt*i);

s1=sin(2*pi*8000*Tt*i);

subplot(411)

plot (i, s), axis([0,1000,-2,2]), set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал с частотой 2000 Гц' )

grid on

subplot(412)

F=filter(numd, dend,s);

plot(i, F),  axis([0,1000,-2,2]), set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал на выходе фильтра')

grid on

subplot(413)

plot (i, s1), axis([0,1000,-2,2]), set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал с частотой 8000 Гц' )

grid on

subplot(414)

F=filter(numd, dend,s1);

plot(i, F),  axis([0,1000,-2,2]), set(gca,'FontName','Times New Roman Cyr','FontSize', 10),

title('Сигнал на выходе фильтра')

grid on

xlabel('Дискретные отсчеты, n')

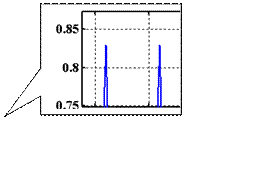
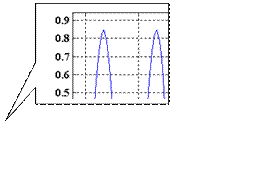
Прямоугольная выноска: Прямоугольная выноска:

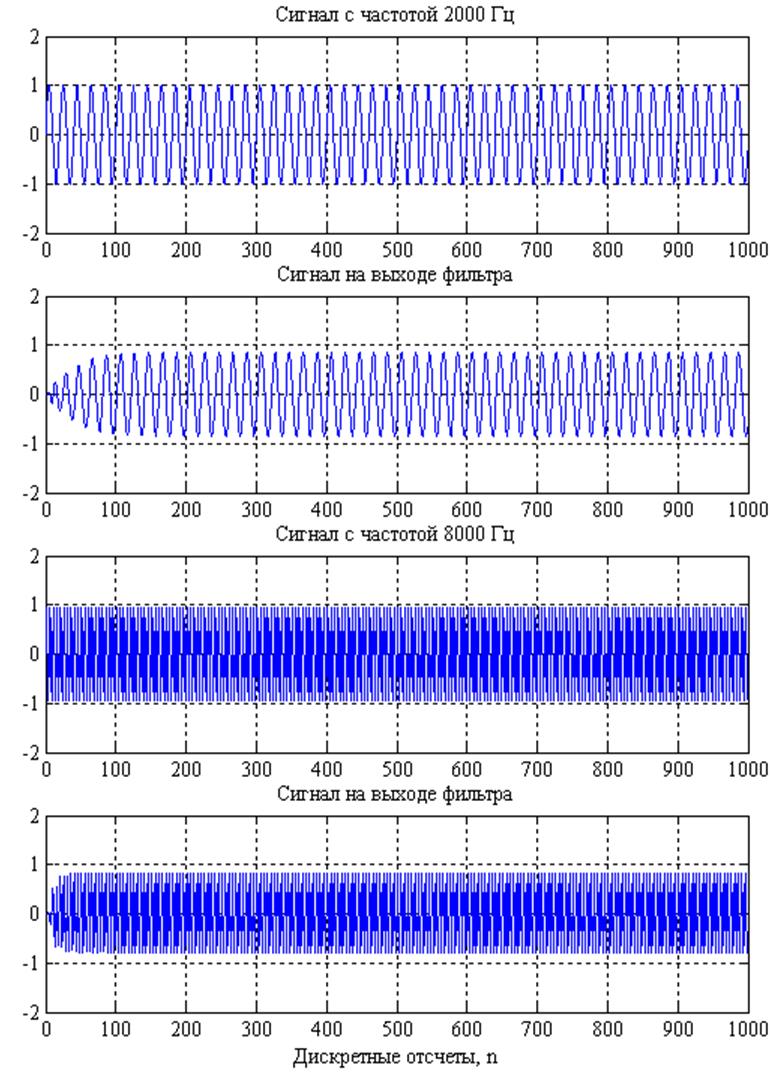
Рис. 14. Выходные сигналы фильтра.

Как видно из представленного графика, что  фильтр пропускает сигналы с частотами 2000 и 8000 Гц, представляющие в спроектированном фильтре верхнюю и нижнюю частоты среза.

Далее, необходимо рассмотреть, как фильтр будет реагировать на сигналы со следующими частотами: 1247 Гц – нижняя граничная частота полосы задерживания и 11000 Гц – частота, которая сходит в переходную полосу фильтра. На рис. 15 приведены графики на выходе фильтра с соответствующими частотами. И судя по ним, можно сказать, что фильтр пропускает их с большим послаблением. Также из графиков видна задержка сигнала на выходе фильтра, обуславливающаяся нелинейностью ФЧХ фильтра.

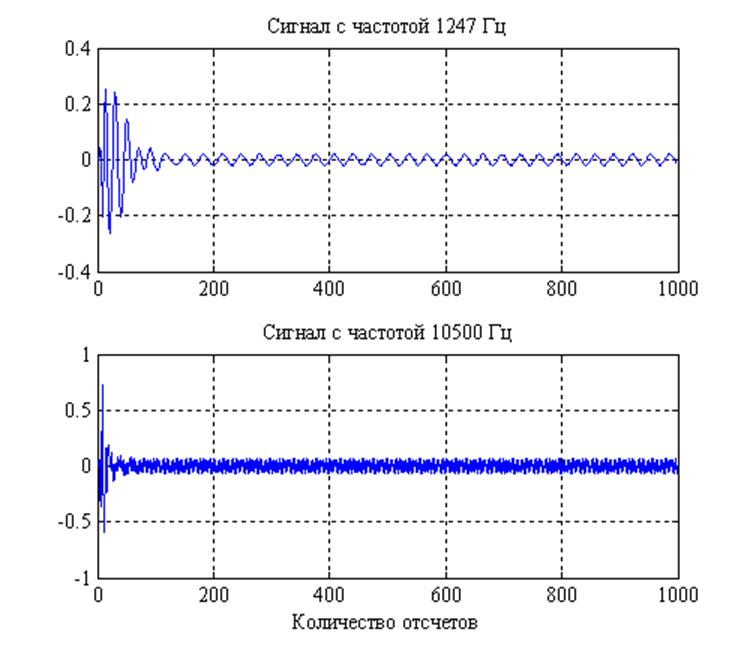
Рис. 15. Выходные сигналы фильтра, при входных с

частотами 1247 Гц и 11000 Гц, соответственно.

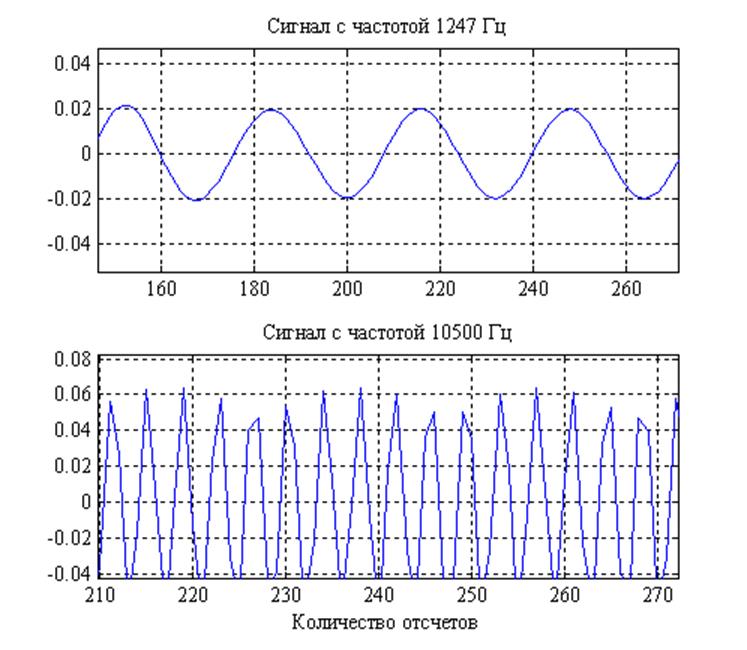
Рис. 16. Выходные сигналы фильтра, при входных с частотами 1247 Гц и 11000 Гц, соответственно (увеличенный масштаб)

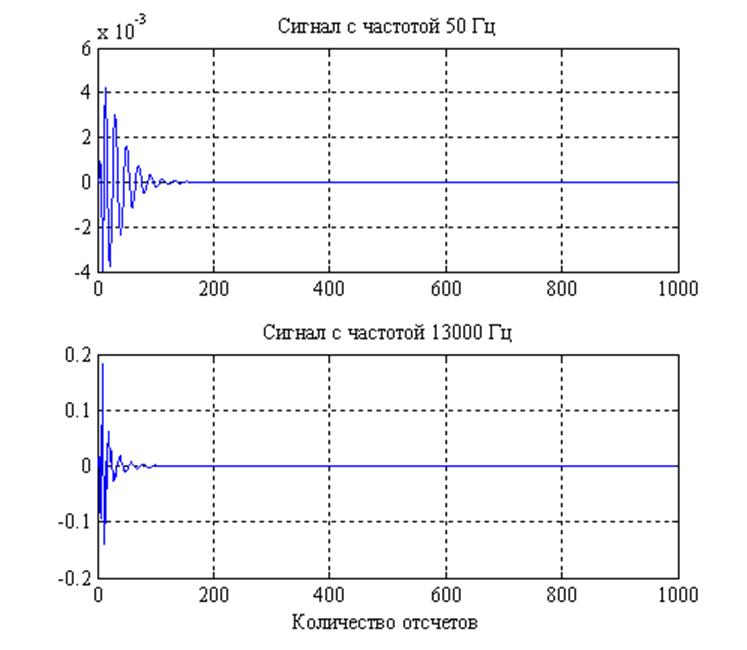
Рис. 17. Выходные сигналы фильтра, при входных с

частотами 50 Гц и 13000 Гц, соответственно.

Фильтр пропускает без искажения гармоники сигнала, входящие в полосу пропускания фильтра (в интервале от 2000 до 8000 Гц),  с допустимым ослаблением (не более 0,707), пропускает те гармоники сигнала, частота которых входит в переходную полосу фильтра (в интервалах от 1247 до 2000 Гц и от 8000 до 11000 Гц), и практически не пропускать гармоники сигнала, находящиеся в полосе задерживания фильтра.


Программирование фильтра и оценка быстродействия

Для реальной оценки быстродействия фильтра разработана программа на языке Visual С++, иллюстрирующая один из примеров реализации фильтра.

В программе за входной сигнал принят уже использованный ранее с частотой 5000 Гц, что входит в полосу пропускания фильтра.

Листинг программы реализации фильтра с комментариями:

#include <iostream.h>

#include <math.h>

#include <windows.h>

#include <stdio.h>

#include <stdlib.h>

#include <time.h>

void sleep( clock_t wait )

{

   clock_t goal;

   goal = wait + clock();

   while( goal > clock() )   ;

}

#define N 5000                     //  Количество отсчетов

#define L 1                              //  Количество раз обработки этих отсчетов

void main()

{

double y[N],x[N]; // определяем  массивы a и b

double a[17]={          1.00000000000000,        -8.677802923343,

36.377624181453,               -98.198275640578,

191.631314325146,              -287.108772148849,

341.728963363368,            -329.485746185612,

259.925095008817,            -168.242894288576,

89.022621415581,               -38.096391080543,

12.927857754314,                -3.364906624499,

0.634202105561,                 -0.077466072584,

0.004634197868

};

double b[17]={         0.00049884915809,            0.00000000000001,

-0.00399079326485,            0.00000000000040,

0.01396777642546,                        0.00000000000205,

-0.027935552855810,            0.00000000000307,

0.03491944106372,                        0.00000000000190,

-0.02793555285419,            0.00000000000046,

0.01396777642641,             0.00000000000005,

-0.00399079326474,            0.00000000000000,            0.00049884915809

};

int Fd=40000;                                 //частота дискретизации

double Td=1/Fd;                  

clock_t start, finish;                                    // обозначаем переменные, работающие со временем

Скачать файл