МИНИСИЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Курсовая работа
по дисциплине “Вычислительная математика”
Факультет: АВТ
Группа: АМ-411
Студент: Ерофеев С. С.
Вариант: 7
Проверил:
Новосибирск, 2006
Содержание
Содержание. 2
1. Задание. 3
2. Вычисление корней многочленов. 4
2.1. Метод Ньютона – Радсона………………………………………………………………………………..4
2.2. Решение алгебраических уравнений методом Лобачевского…………………………………….11
3. Решение обыкновенных дифференциальных уравнений (ОДУ) 18
3.1. Метод Адамса……………………………………………………………………………………………...18
3.2. Метод Адамса – Крылова………………………………………………………………………………...29
4. Заключение. 34
5. Литература. 36
Курсовая работа содержит две задачи из различных разделов вычислительной математики.
Первая задача посвящена вычислению корней многочлена p(x) = x6 + 5x5 – 7x4 + 3x3 – 6x2 + x +12 различными методами, такими как: метод Ньютона - Радсона; метод Лобачевского, который в свою очередь включает в себя метод квадрирования и использование формулы Энке.
Вторая задача посвящена решению обыкновенных дифференциальных уравнений такими методами, как метод Адамса и метод Адамса - Крылова.
В заключительной части работы должны быть приведены результаты сравнения расчетов с результатами, полученными на основе применения математического пакета (любого из доступных) для непосредственного решения задачи. Должны быть сделаны выводы о проведенной работе, отмечены недостатки и достоинства алгоритмов, указаны (по возможности) перспективы развития проблем, связанных с данной задачей.
В основе метода лежит хорошо известный метод касательных (метод Ньютона):
|
|
Этот метод позволяет
построить итерационную последовательность, сходящейся к корню уравнения ![]() . Как известно, для этого надо иметь
достаточные условия сходимости (теорема 1).
. Как известно, для этого надо иметь
достаточные условия сходимости (теорема 1).
Теорема 1. Пусть ![]() определена и дважды дифференцируема
на
определена и дважды дифференцируема
на ![]() , причем
, причем ![]() ,
а производные
,
а производные ![]() ,
, ![]() сохраняют
знак на
сохраняют
знак на ![]() . Тогда, исходя из начального
приближения
. Тогда, исходя из начального
приближения ![]() , удовлетворяющего неравенству
, удовлетворяющего неравенству ![]() , можно построить последовательность
, можно построить последовательность ![]() 0, 1, 2, … , сходящуюся к
единственному на
0, 1, 2, … , сходящуюся к
единственному на ![]() решению
решению ![]() уравнения
уравнения ![]() .
.
Для оценки погрешности n-го приближения корня можно воспользоваться неравенством
|
|
где ![]() — соответственно,
значения наименьшей по модулю первой производной, и значение наибольшей второй
производной на отрезке
— соответственно,
значения наименьшей по модулю первой производной, и значение наибольшей второй
производной на отрезке ![]() .
.
Если задана погрешность ![]() вычисления корня (т. е. корень
вычисляется с точностью
вычисления корня (т. е. корень
вычисляется с точностью ![]() ), то итерационный
процесс может быть прекращен, когда выполняется условие
), то итерационный
процесс может быть прекращен, когда выполняется условие
|
|
В этом случае величина ![]() принимается за приближенное значение
корня, вычисленного с точностью
принимается за приближенное значение
корня, вычисленного с точностью ![]() .
.
Метод Ньютона (иногда его называют методом Ньютона-Радсона) наиболее эффективен, если известно хорошее начальное приближение для корня и в окрестности корня график функции имеет большую крутизну, что обеспечивает быструю сходимость метода.
Процесс нахождения корней
полинома ![]() по методу Ньютона имеет итерационный
характер и состоит в понижении степени многочлена за счет удаления найденных
уже корней. Пусть, например, найден один корень
по методу Ньютона имеет итерационный
характер и состоит в понижении степени многочлена за счет удаления найденных
уже корней. Пусть, например, найден один корень ![]() (действительный).
Тогда многочлен
(действительный).
Тогда многочлен ![]() можно разделить (без
остатка) на
можно разделить (без
остатка) на ![]() :
:
|
|
и задача сводится к отысканию корней многочлена,
степень которого на единицу меньше степени многочлена ![]() .
.
Метод Ньютона (применительно для полинома)
|
|
позволяет находить комплексные корни. В этом
случае многочлен будет делиться без остатка на ![]() ,
где
,
где ![]() и
и ![]() —
коэффициенты пары комплексных (сопряженных) корней
—
коэффициенты пары комплексных (сопряженных) корней ![]() и
и
![]() .
.
Таким образом, можно последовательно определить все корни многочлена.
|
Задан полином: |
|
|
|
|
|
|
|
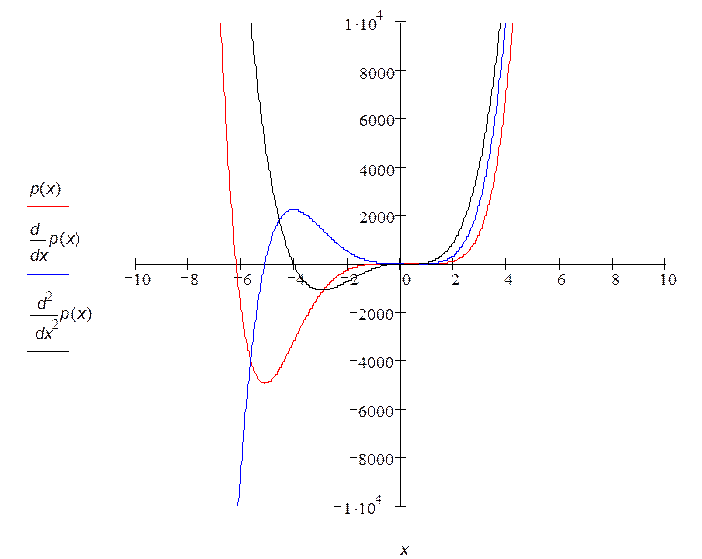
Отделим графически действительные корни p(x) = 0. |
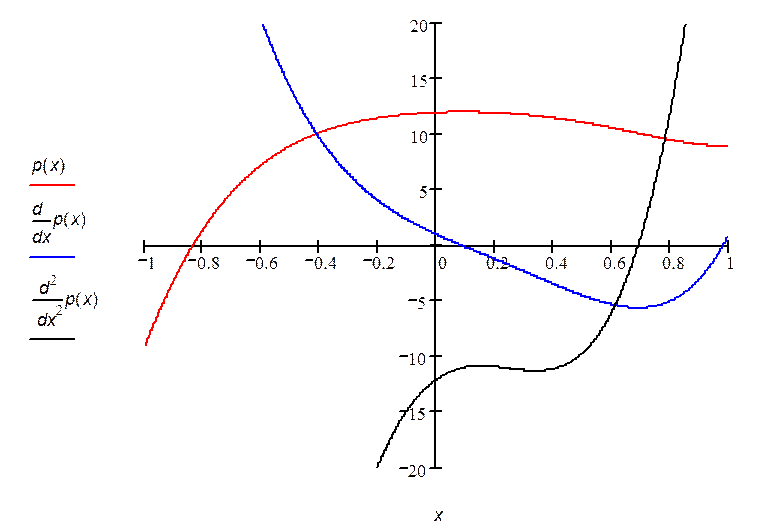
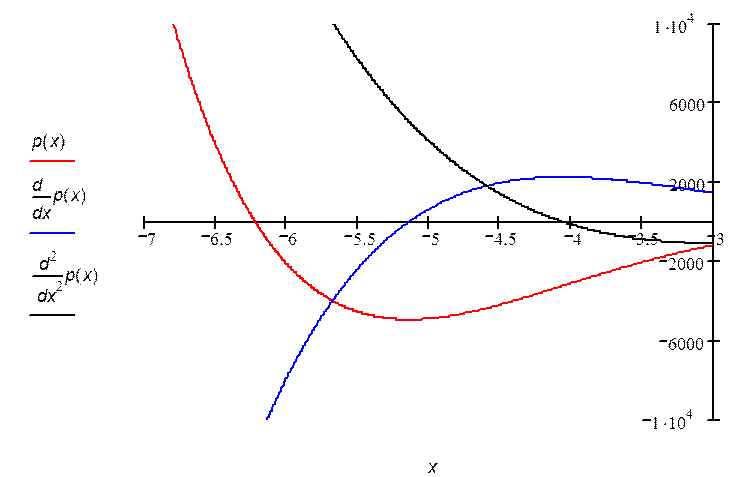
|
По графику p(x) и результатам трассировки графика определяем, что один из действительных корней полинома располагается на интервале [-0.85;-0.8], второй - на интервале [-6.5;-6]. |
|
Убедимся, что на заданном отрезке p(x) удовлетворяет условиям сходимости метода Ньютона. |
|
p(x) определён на [-0.85;-0.8] и дважды дифференцируем на [-0.85;-0.8] p(x) определён на [-6.5;-6] и дважды дифференцируем на [-6.5;-6] |
|
|
|
|
|
|
|
|
|
|
|
(меньше нуля) |
|
|
|
Первая и вторая производная сохраняют свой знак на [-0.85;-0.8]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Первая и вторая производная сохраняют свой знак на [-6.5;-6]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее произведём выбор значения e для условия окончания итерационного процесса |
|
Запрограммируем метод Ньютона: |
|
|
|
|
|
|
|
|
|
Найден действительный корень. Многочлен p(x) можно разделить без остатка на (x-x1). Задача сводится к отысканию корней многочлена, степень которого на единицу меньше степени многочлена p(x), |
|
|
|
|
|
|
|
|
|
Далее: |
|
|
|
|
|
Поскольку для любого x на интервале [-10;10] полином p3(x) > 0, то p3(x) на интервале [-10;10] не удовлетворяет условиям сходимости метода Ньютона, и процесс нахождения корней следует прекратить. |
|
Чтобы определить комплексные корни данного многочлена, воспользуемся методом Ньютона - Радсона, но в качестве первого приближения будем использовать определённое комплексное число |
|
|
|
Первая пара сопряжённых корней: |
|
|
|
|
|
|
|
|
|
Вторая пара сопряжённых корней: |
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.