Вычисление корней многочлена p(x) = x6 + 5x5 – 7x4 + 3x3 – 6x2 + x +12 различными методами. Решение обыкновенных дифференциальных уравнений, страница 2

Сравним найденные корни с корнями, полученными с помощью стандартной функции Mathcad:

Возвращает все корни уравнения (с использованием метода ЛаГуэрре (LaGuerre))

Действительные корни, найденные с помощью метода Ньютона-Радсона:

Комплексные корни, найденные с помощью метода Ньютона-Радсона:

Корни, найденные с с помощью метода Ньютона-Радсона, с точностью до 0.001 совпадают с корнями, найденными с помощью стандартной функции Mathcad.

2.2. Решение алгебраических уравнений методом Лобачевского

Метод Лобачевского считался (до середины 50-х годов) одним из самых совершенных способов решения нелинейных алгебраических уравнений, благодаря следующим достоинствам метода:

1) решение уравнений производится без выполнения громоздких операций по предварительному отделению корней;

2) все корни уравнения определяются практически одновременно;

3) определяются различные типы корней — действительные и комплексные;

4) корни вычисляются, как правило, с весьма высокой точностью;

5) процесс вычислений всегда сходится.

Вместе с тем он не нашел широкого применения при реализации на ЭВМ из-за недостатков:

1) метод недостаточно универсален;

2) громоздкость алгоритмического описания;

3) недостаточно высокая точность определения корней с близкими и равными модулями.

Для устранения отмеченных недостатков разработано несколько его вариантов, которые, впрочем, не свободны от дополнительных недостатков.

В свою очередь метод Лобачевского включает в себя метод квадрирования и применение формул Энке для отыскания комплексных корней. Остановимся на этих методах поподробнее.

Метод Энке

Этот метод был предложен немецким математиком и астрономом Энке для уравнений любой четной степени.

Формулы Энке имеют следующий вид:

а) n = 4

б) n = 6. Для уравнения 6-ой степени:

Аналогичные формулы можно построить и для уравнений четных степеней, больших 6.

Искомая величина t в уравнениях является общим корнем обоих уравнений Энке, поэтому определив t, находим значение действительной и мнимой части комплексного корня:

Уравнение Энке (при n = 4) можно использовать также и в случае двух пар действительных корней.

Кроме того, для уравнений нечетных степеней можно применять этот метод, предварительно исключив действительный корень.

И наконец, важным достоинством метода является то обстоятельство, что погрешности определения корней не оказывают влияния на погрешности определения других корней.

Метод квадрирования

Этот метод предложен Белановым А. А. Сущность этого метода в следующем. После m циклов квадрирования определяют квадратные уравнения, содержащие комплексные корни.

Затем с помощью формул Лобачевского преобразуют одно из квадратных квадрированных уравнений m-го цикла в уравнение, соответствующее предыдущему (m–1) циклу, т. е. в уравнение

Этот метод целесообразно применять при большом различии между модулями корней, и он требует информации о знаках коэффициентов в каждом цикле квадрирования. В случае, если модули комплексных корней близки или равны, то для обеспечения большого различия между модулями является разложение по степеням двучлена , где 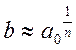, с помощью схемы Горнера, причем знак коэффициента b соответствует знаку .