Методы аппроксимации и интерполяции функций. Вариант 3

Министерство образования и науки Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра ВТ

Лабораторная работа №6

«Методы аппроксимации и интерполяции функций»

Студент:                                                                                                                   Преподаватель:

Кириллова Мария                                                                                                   Рабинович Е.В.

Группа: АТ – 93

Вариант №3

Новосибирск - 2011

Цель работы:

Научиться методам аппроксимации и интерполяции с помощью методов кубического сплайна и тригонометрической интерполяции.

Для достижения цели лабораторной работы мы должны выполнить следующие задания:

Задание 1:

Вычислить значения заданной функции  в узлах интерполяци  на отрезке . Из вычисленных значений построить таблицу и по ней построить интерполяционный кубический сплайн , вычислить его значения в промежуточных точках . Сравнить вычисленные значения с точными значениями функции в точках . Построить графики  и .

Задание 2:

Построить интерполяционный тригонометрический многочлен, аппроксимирующий функцию , заданную таблицей значений в точках   .

С помощью полученного полинома вычислить значение функции и в точках

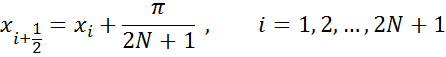
Ход работы:

Метод аппроксимации с помощью кубического сплайна.

Начальные условия:

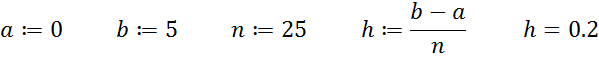
Пусть. Зададимся опорными точками, которые вычисляются по формуле:

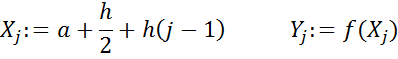
Получаем таблицу значений:

-0.1	0.9049882
0.1	1.1049868
0.3	1.3438252
0.5	1.6151463
0.7	1.9044965
0.9	2.1887419
1.1	2.4380715
1.3	2.6210059
1.5	2.711481
1.7	2.6957186
1.9	2.5761604

Производная функции в нулевой опорной точке:

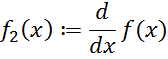
С помощью программы Spline вычисляем сплайн-коэффициенты:

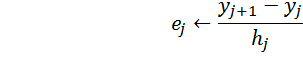
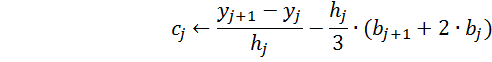
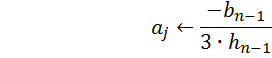
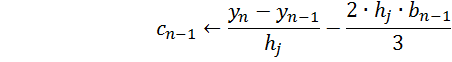
При помощи функции Functionвычисляем значения кубического сплайна в узлах интерполяции:

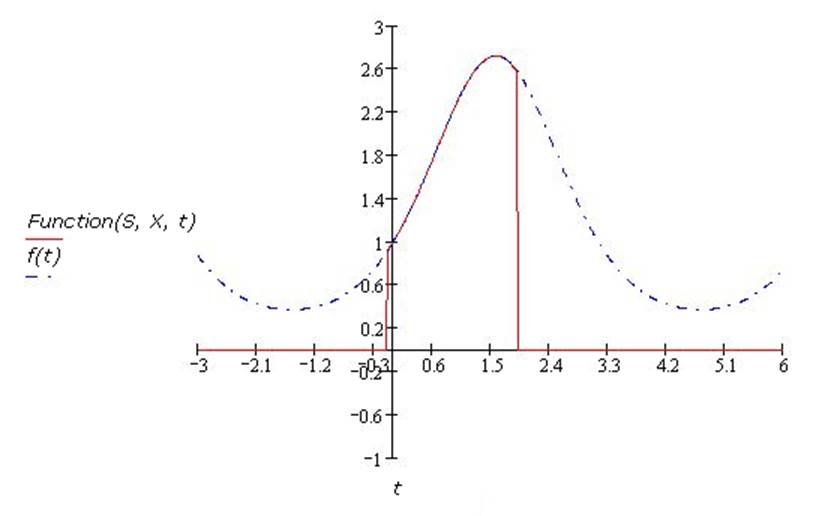
Построим графики реальной  и аппроксимированной  функции по значениям сплайна.

		При данном n значения реальной и аппроксимированной функций совпадают вплоть до 8го порядка. При больших nточность вычисления возрастает. Это говорит о высокой эффективности интерполирования с применением сплайн-функции.
0.90498816	0.90498816
1.10498683	1.10498683
1.34382524	1.34382524
1.6151463	1.6151463
1.90449653	1.90449653
2.18874191	2.18874191
2.43807151	2.43807151
2.62100593	2.62100593
2.71148102	2.71148102
2.6957186	2.6957186
2.57616044	2.57616044

Метод интерполирования тригонометрическими многочленами.

Построим интерполяционный тригонометрический полином, аппроксимирующий функцию, заданную в точках

n		Коэффициенты тригонометрического многочлена  : -тригонометрический многочлен;
1	-1.24
2	-1.17
3	-1.08
4	-0.96
5	-0.84
6	-0.79
7	-0.8
8	-0.9
9	-1.1
10	-1.21
11	-1.02
12	-1.28
13	-1.32
14	-1.34
15	-1.36
16	-1.37
17	-1.37
18	-1.36
19	-1.35
20	-1.33
21	-1.3

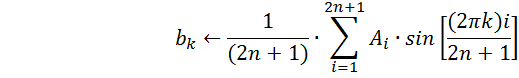
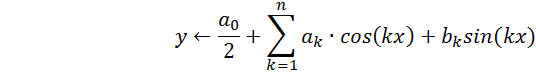
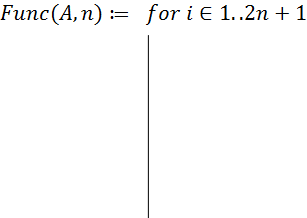
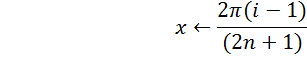
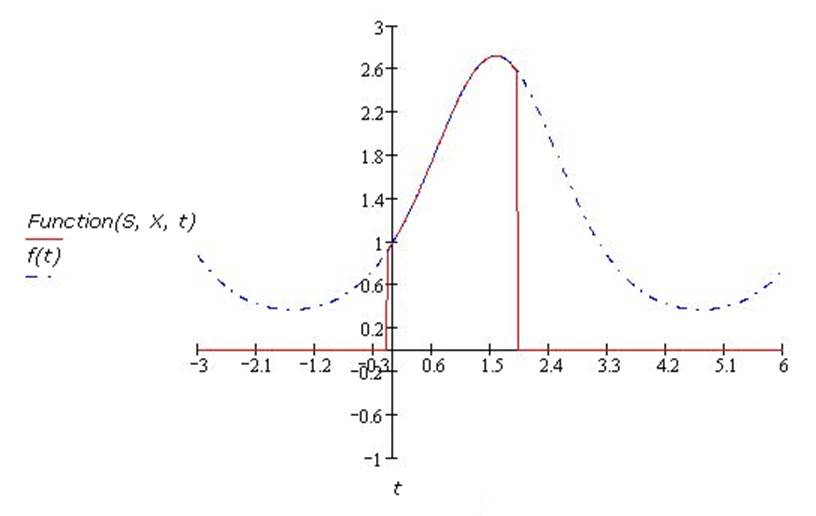
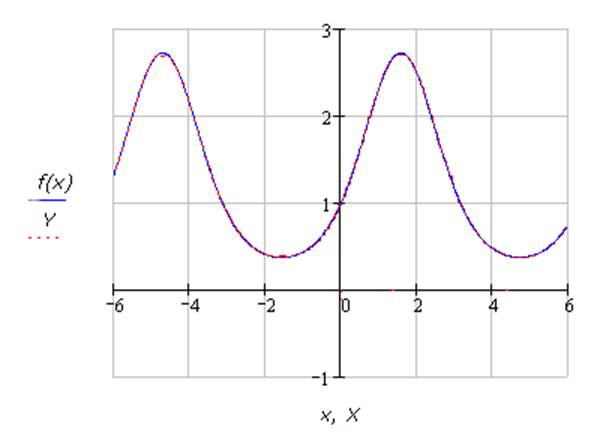
Построим графики реальной функции  и функции Y, полученной с помощью аппроксимации тригонометрическим многочленом. Сравнивая эти графики, можно сказать, что при данном значении n аппроксимированная функция не совпадает с реальной.

Вывод:

Сравнение результатов приближения функции различными методами.

О точности приближения сплайн методом выше было сказано, что для заданного nпозволяет вычислять значения функции с точностью до 8-го знака (и выше). Тригонометрическая же интерполяция дала малую точность вычисления, т.е. для данной функции оказалась неэффективна. Так как результаты применения методов были удовлетворительны, то для их проверки не использовались встроенные функции интерполирования.