МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ВТ
 |
Расчётно-графическая работа
по дисциплине «Вычислительная математика»
Вариант 16
Факультет: АВТ
Группа: АМ-311
Студент: Трофимов А.В.
Преподаватель: Рудковский В.П.
НОВОСИБИРСК 2005
Содержание.................................................................................................................................... 2
Задача №1. «Приближение функции различными методами»................................................ 3
Метод наименьших квадратов, классический вариант........................................................ 3
Метод наименьших квадратов с использованием ортогональных многочленов Чебышева. 15
Метод интерполирования с применением сплайн-функций.............................................. 18
Метод интерполирования тригонометрическими многочленами..................................... 21
Сравнение результатов приближения функции различными метолами.......................... 23
Задача №2. «Численные методы интегрирования»................................................................. 24
Численное интегрирование с использованием сплайн-функции...................................... 24
Метод трапеций....................................................................................................................... 26
Метод Симпсона..................................................................................................................... 29
Сравнение результатов интегрирования функции различными методами...................... 30
Задача №3. «Нахождение числовых значений производных функций численным методом». 31
Использование первой интерполяционной формулы Ньютона для вычисления производных функций.................................................................................................................................................... 31
Заключение.................................................................................................................................. 39
Список литературы..................................................................................................................... 40
При использовании классической формы МНК возникает необходимость повысить степень полинома, если вычисленные с его помощью коэффициенты сильно отличаются от наблюдаемых. В этом случае следует производить пересчёт всех коэффициентов Аi, полученных ранее.
Для данной функции f(x)=1/(1+x2) на интервале от a=1 до b=6 получаем:
|
Число узлов интерполирования: |
|
|
|
Начальная степень полинома: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Промежуточные точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
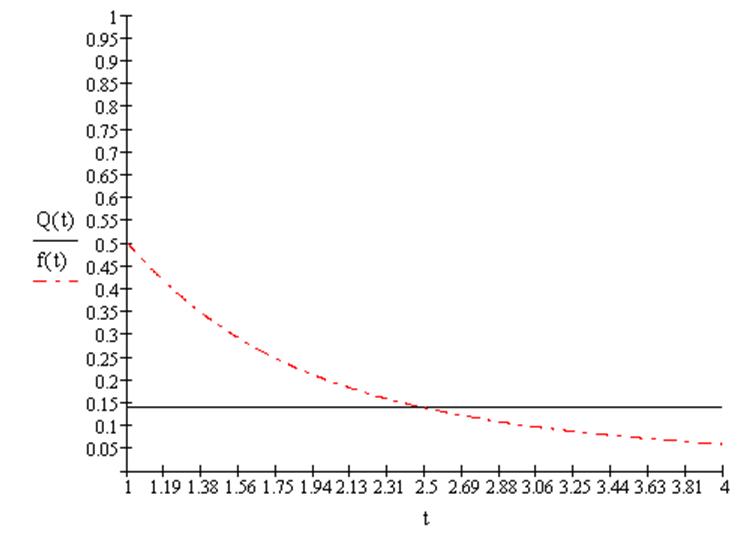
Величина остатков достаточно велика, поэтому будем искать полином первой степени (все расчёты аналогичны).
|
Степень полинома: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Промежуточные точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
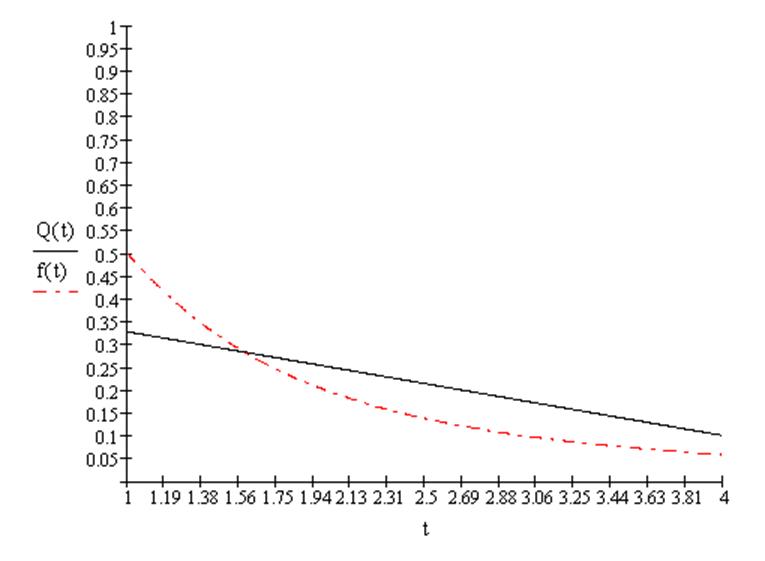
Величина остатков dy по-прежнему слишком велика по сравнению с заданной точностью, поэтому будем искать полином второй степени.
|
Степень полинома: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Промежуточные точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим полином 3-й степени: |
|
Степень полинома: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
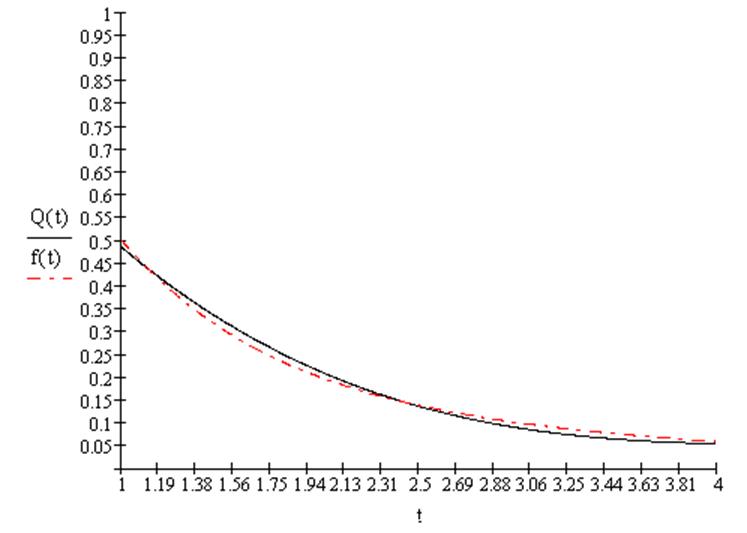
|
Промежуточные точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
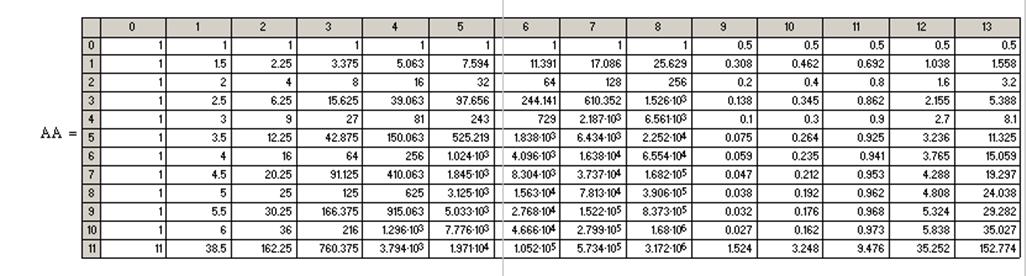
Полином 4-й степени: |
|
Степень полинома: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
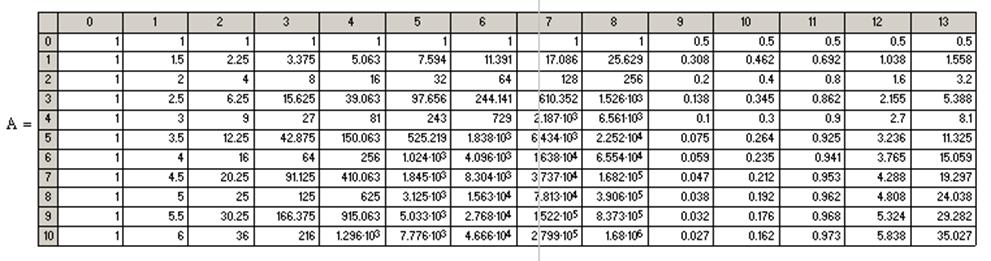
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Промежуточные точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.