Метод наименьших квадратов с использованием ортогональных многочленов Чебышева даёт ещё более точный результат вычислений. При той же степени полинома (m=4) метод Чебышева даёт простое отклонение около 0.001. Квадратичное же отклонение, естественно, будет ещё меньше.
О точности приближения сплайн-методом было уже сказано выше. Этот метод для заданного n позволяет вычислять значения функции с точностью до 8 знака (и выше).
Тригонометрическая интерполяция даёт малую точность вычисления. Это связано с небольшим значением n. При увеличении n точность заметно возрастает.
Нам известно, что кубический сплайн приближает исходную функцию f(x) на интерполяционной сетке x0<x1<…<xn с высокой точностью. Поэтому интеграл можно приближённо вычислить по формуле:
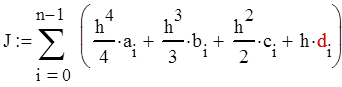 |
Зададимся опорными точками:
|
|
Значение интеграла функции f(x)=1/(1+x2) на интервале [a;b] равно:
|
|
|
|
|
|
|
|
Значение интеграла, вычисленного с использованием сплайн функции:
|
|
|
|
Погрешность вычисления составляет:
|
|
|
|
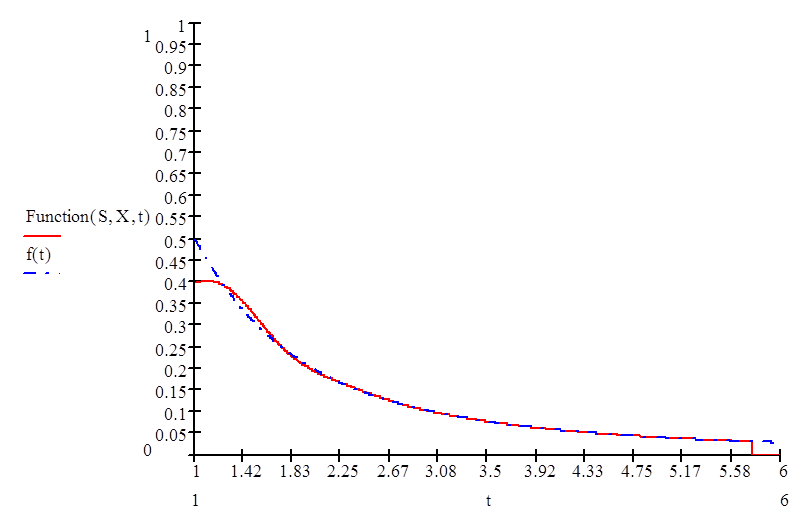
Эта погрешность отражена на графике:
 |
Решение задачи вычисления интеграла методом трапеций заключается в разбиении отрезка [a;b] на множество отрезков меньших размеров и вычислении интеграла как суммы, приближённо вычисленных площадей полосок, получившихся при таком разбиении (см. рис. 1).
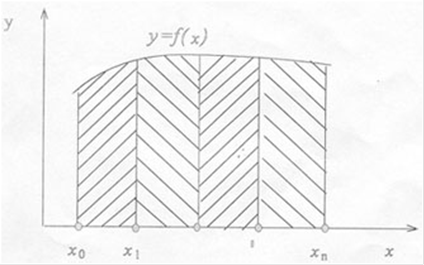
Рис. 1
Таким образом величину определённого интеграла можно оценить по следующей формуле:
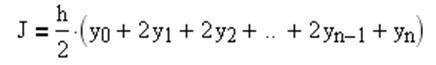
Исходные данные:
|
|
|
|
|
|
|
|
|
|
|
|
Реальное значение интеграла (вычисленное в среде MathCAD):
|
|
|
|
Вычисление интеграла методом трапеций:
|
|
|
|
|
|
Как видно, метод трапеций даёт отклонение от реального значения.
|
|
|
|
Ошибку ограничения метода трапеций можно вычислить по следующей формуле:
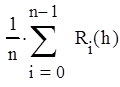
где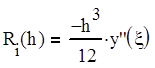 , а
, а
|
|
|
x |
|
(xi ,xi+1). |
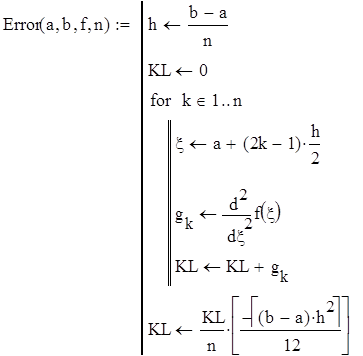 |
|
|
![]()
- значение ошибки
Окончательное значение функции с учётом ошибки:
|
|
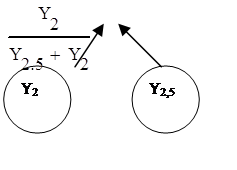
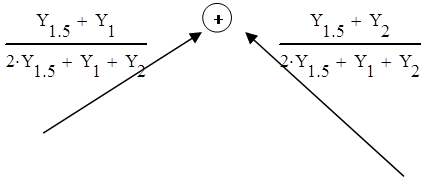
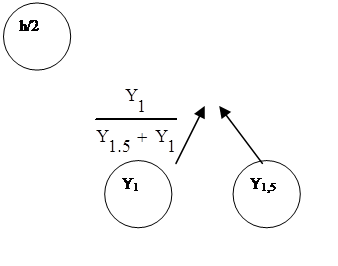
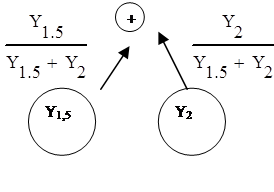
Граф вычислительного процесса:
 |
![]() +1
+1
 |
|||||
+1
 |
|||
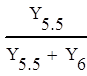 |
|||
![]()
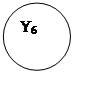
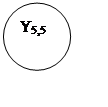 * * *
* * *
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||

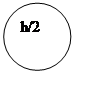 +1
+1
 |
+1
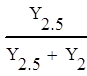


 |
|||||
 |
|||||
 +1
+1

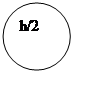
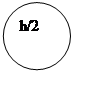
![]()
 +1
+1
![]() +1
+1
![]()
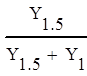
 +1
+1
 |
|||
 |
|||
Для правила Симпсона в качестве функции, с помощью которой осуществляется приближение исходной функции на частичных отрезках интегрирования, выбрана парабола. Это позволяет уменьшить ошибку интегрирования по сравнению, например, с методом трапеций, в котором приближение на отрезках осуществляется линейными функциями.
Формула для вычисления интеграла по методу Симпсона имеет следующий вид:
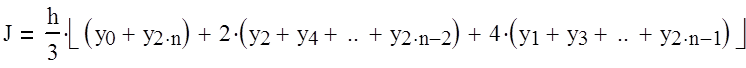
Начальные условия:
|
|
|
|
|
|
|
|
|
|
|
|
Реальное значение интеграла:
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.