Математика \ Вычислительная математика

Приближение функции различными методами. Численные методы интегрирования. Поиск числовых значений производных функций численным методом, страница 4

Процедура для вычисления интеграла по методу Симпсона:

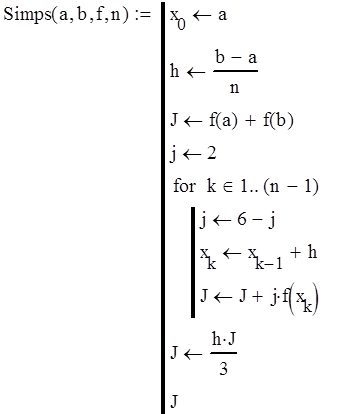
Значение интеграла, вычисленного по методу Симпсона:

Разность между реальным значением интеграла и вычисленным по методу Симпсона составляет:

Как видно, метод Симпсона даёт более точный результат, чем метод трапеций.

Вычисление ошибки метода Симпсона осуществляется по формуле:


Процедура для вычисления ошибки:

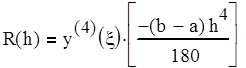
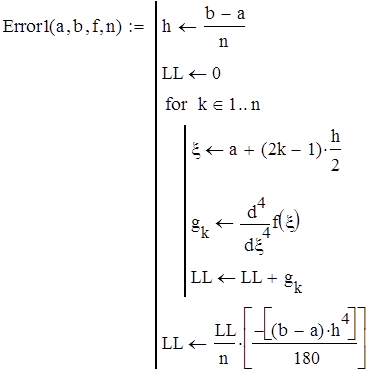Ошибка составляет:

- окончательное значение интеграла по методу Симпсона

Сравнение результатов интегрирования функции различными методами.

Метод интегрирования с использованием сплайн-функции даёт относительно большую погрешность вычисления при малых значениях n (по сравнению с методами трапеций и Симпсона). Погрешность составляет 0.047.

Метод трапеций даёт более точный результат. Ошибка этого метода составляет –0.01.

Наиболее точным из предложенных методов интегрирования является метод Симпсона. Ошибка метода Симпсона – порядка 10-5.

Задача №3. «Нахождение числовых значений производных функций численным методом».

Использование первой интерполяционной формулы Ньютона для вычисления производных функций.

Первая интерполяционная формула Ньютона для вычисления производных имеет вид:

y(x)=y0+q.∆y0+q.(q-1). ∆2y0/2!+…+ q.(q-1).….(q-n+1). ∆ny0/n!

где q=(x-a)/h.

Учитывая, что dy/dx=dy/dq=dq/dx=1/h.dy/dq получаем:

y’(x)=1/h.( ∆y0+(2q-1).∆y20/2+(3q2-6q+2).∆y30/3+…).

Для вычисления второй производной получаем:

y’’(x)=1/h2.( ∆2y0+(q-1).∆y30/3+(6q2-18q+11). ∆y40+…).

Производная функции в точке вычисляется по следующей формуле (с учётом того, что q=0):

y’(xi)=1/h.(∆yi-∆2yi/2+∆3yi/3+…), где ∆jyi – коэффициенты, взятые из матрицы разностей.

Аналогично считается вторая производная:

y’’(xi)=1/h2.( ∆2yi-∆3yi+11/12. ∆4yi+…)

Задаим начальные условия:

- процедура составления матрицы значений х в узлах

и значений f(x)



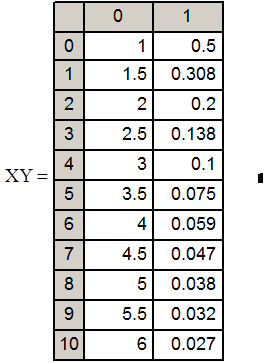Процедура, задающая матрицу разностей из коэффициентов ∆jyi для подсчёта значений производных в точках xi:

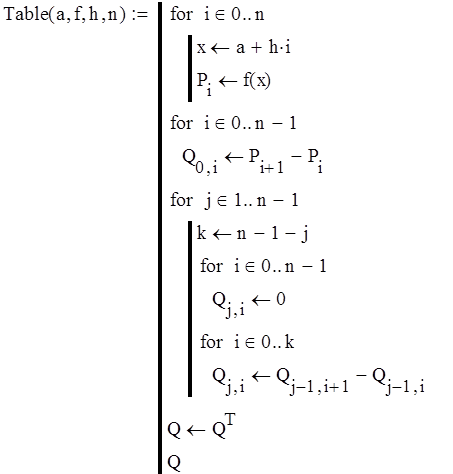-  подсчёт коэффициентов при ∆jyi для вычисления первой производной в точке xi

 

 

 

Функция вычисления значения первой производной:

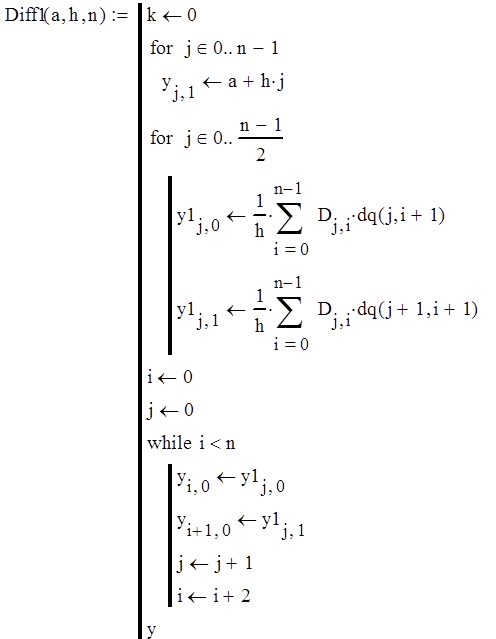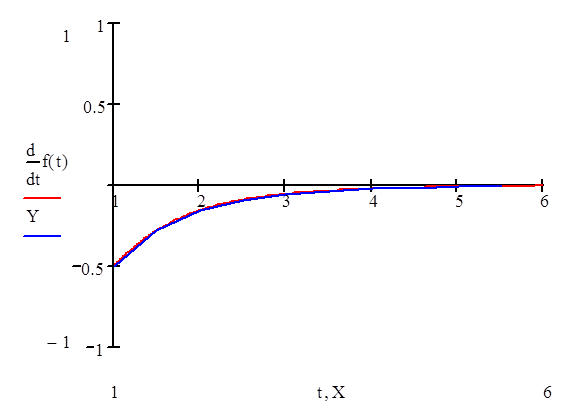
Построим графики производных, вычисленных процедурой Diff1 и встроенной функцией MatCAD:


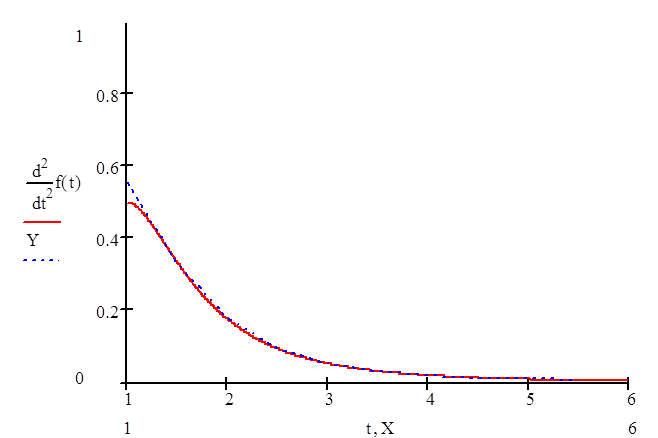
Аналогично для второй производной:






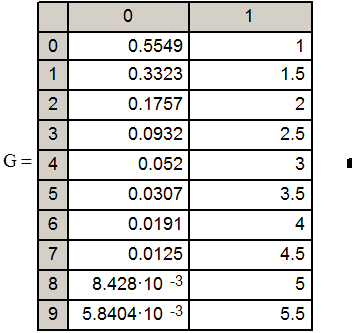
Погрешность для вычисленя первой производной:

где Rxi – ошибки в точках xi.

Погрешность для вычисления второй производной:

Как видно из таблиц, точность вычисления производных достаточно велика. Ошибка находится впределах @10-7…10-4.


Заключение.

Численные методы, исследованию которых была посвящена расчётно-графическая работа, в большинстве случаев позволяют нам найти решение той или иной задачи.

При выполнении расчётно-графической работы было проведено приближение заданной функции различными методами. Наиболее приемлеемыми для данного случая оказались методы наименьших квадратов с использованием ортогональных многочленов Чебышева и сплайн-интерполяции. Эти методы дают наименьшую погрешность вычислений.

 Численное интегрирование функции было осуществлено тремя методами. Явный приоритет имеет метод Симпсона, для которого погрешность составляет порядка 10-5. Построен граф вычислительного процесса для метода трапеций.

Численное дифференцирование функции с использованием первой интерполяционной формулы Ньютона даёт достаточно неплохой результат для первой и второй производных. Ошибка составляет порядка 10-7…10-4.


Список литературы.

1. Волков Е.В.  Численные методы: Учеб. Пособие для вузов.- 2-е изд.,испр. –М.: Наука, Гл. физ.-мат. Лит.,1987.-248с.

2. Баврин И. И. Высшая Математика. – М.: Издательский центр “Академия” Высшая Школа, 2000

3. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, Гл. физ.-мат. лит.,1989.-432с.

4. Методические указания к лабораторным работам по дисциплине “Вычислительная математика”.

Скачать файл