Приближение функции различными методами. Численные методы интегрирования. Поиск числовых значений производных функций численным методом, страница 2

Метод наименьших квадратов с использованием ортогональных многочленов Чебышева.

Суть метода Чебышева состоит в том, что приближающий многочлен находится (строится) в виде суммы многочленов, выбранных специальным образом:

где , , и вообще:

Зададим начальные условия:

Перейдём теперь к построению самих многочленов. Эти многочлены строятся рекурсивным путём на основе применения рекуррентной формулы второго порядка, позволяющей вычислять следующий многочлен по двум предыдущим.

Значения, полученные при аппроксимации полиномами различных степеней (0,1,2,3,4) заданной функции и отклонения от точных значений:

Метод интерполирования с применением сплайн-функций.

Специальным видом кусочной интерполяции является интерполяция с помощью сплайн-функции. Образованные в процессе такой интерполяции кривые обладают достаточным приближением и образуют кусочно-кубический полином. Сплайн-интерполяция по сравнению с другими методами интерполяции обеспечивает наилучшее приближение.

Исследуем интерполяцию кривой f(x)=1/(1+x²) в интервале [1;6].

Пусть, j=0…10. Зададимся опорными точками (они вычисляются по формуле:

X_j=a+h/2+h(j-1)).

- получаем таблицы значений

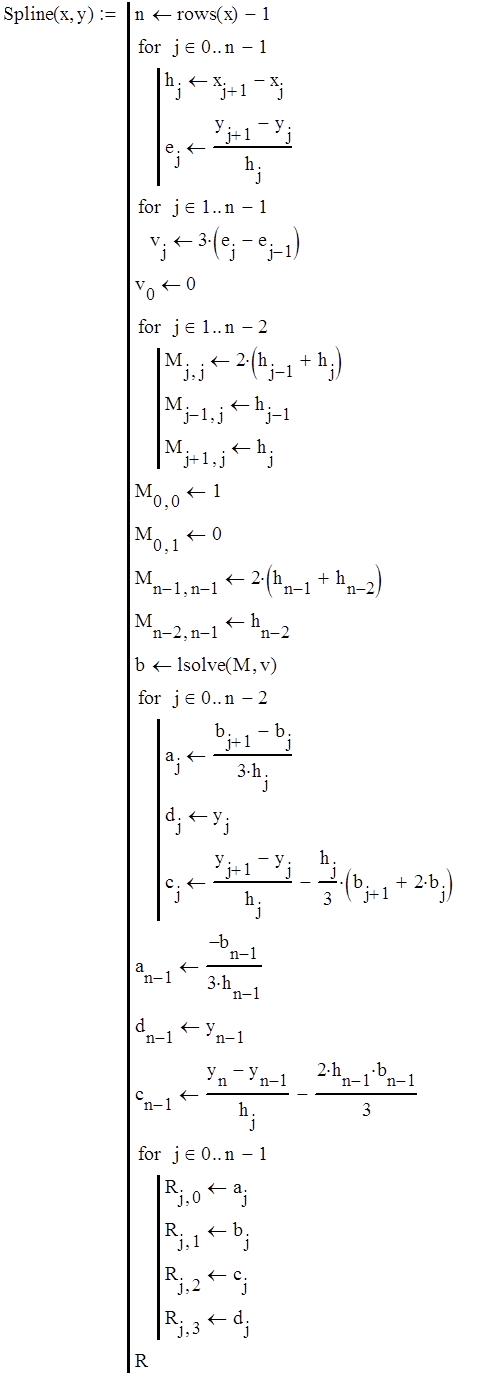
Построим графики реальной и аппроксимированной функций в заданном интервале:

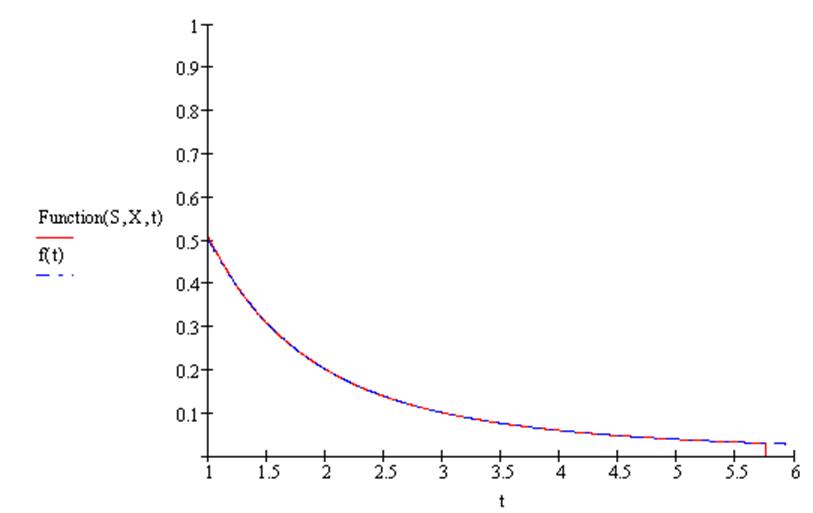
Сравним таблицы значений:

При данном n значения реальной и аппроксимированной функций совпадают вплоть до 8-го порядка. При больших n точность вычисления возрастает. Это говорит о высокой эффективности интерполирования с применением сплайн-функции.

Метод интерполирования тригонометрическими многочленами.

Задача тригонометрической интерполяции состоит в построении тригонометрического интерполяционного многочлена наименьшей степени, удовлетворяющего условиям Pм(x_i)=f(x_i), i = l,…, 2n+1.

Решением этой задачи является тригономет­рический многочлен

         ,

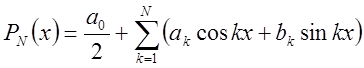коэффициенты которого вычисляются по следующим формулам:

        

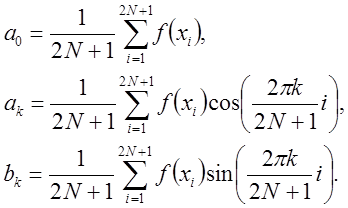
Широкие возможности тригонометрической интерполяции сле­дуют из того факта, что с возрастанием n многочлен Р(х) аппроксимирует f(x) с возрастающей точностью, т. е.

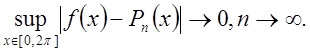
В нашем случае (согласно заданию) n берётся небольшим (n=6-8), поэтому велика погрешность вычислений.

Зададим таблицу значений и n:

Эта таблица значений взята из предыдущего метода интерполяции с применением кубического сплайна (таблица значений f(X_j)).

Получим тригонометрический многочлен:

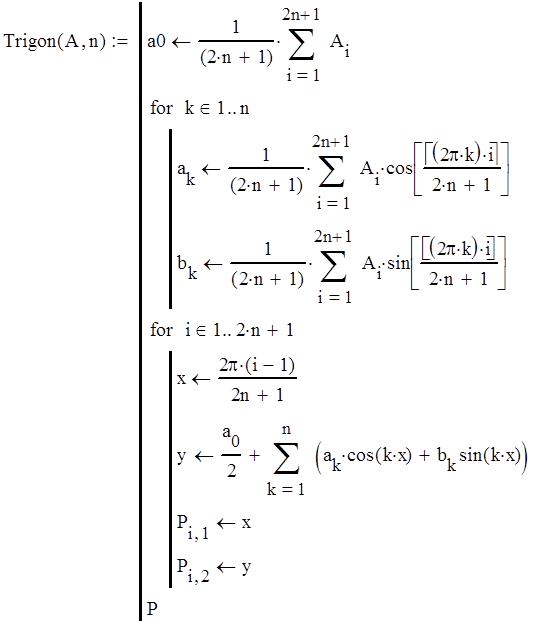
Построим графики реальной функции f(x), функции, полученной с помощью аппроксимации тригонометрическим многочленом, а также с помощью функции Func(A,n). Даже сравнивания эти графики, можно заключить, что при данном значении n аппроксимированные функции не совпадают с реальной, хотя и повторяют её контуры.

Сравнение результатов приближения функции различными метолами.

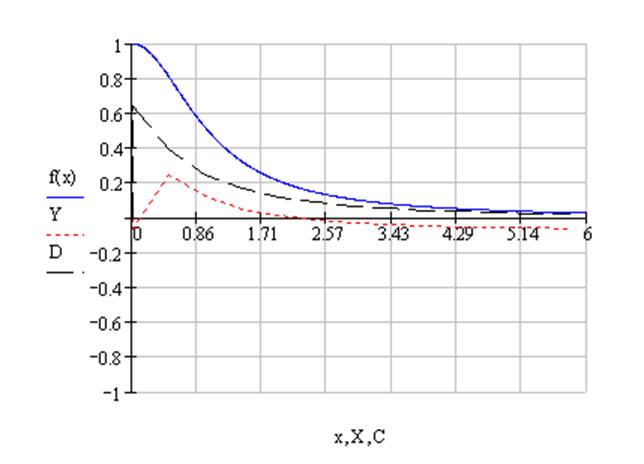
Метод наименьших квадратов (его классический вариант) даёт достаточно хороший результат. Уже при степени полинома равной четырём квадратичное отклонение равно 0.00011639.