Многочлены
Многочленом (или полиномом) степени n от переменного z (комплексного или вещественного) называется выражение вида
![]() ,
,
где ![]() - коэффициенты
полинома.
- коэффициенты
полинома.
Рассматриваемые в технических задачах полиномы имеют вещественные (действительные) коэффициенты.
Корень многочлена (нуль) – это
число λ, при котором ![]() .
.
Согласно основной теореме алгебры комплексных чисел C всякий многочлен ненулевой
степени с любыми числовыми коэффициентами имеет хотя бы один действительный или
комплексный корень. Число λ является корнем многочлена a(z) тогда и только
тогда, когда a(z)
делится без остатка на z – λ. Если a(z) делится без остатка
на ![]() , но не делится на
, но не делится на ![]() , то λ является k – кратным корнем или
корнем кратности k многочлена
a(z). Корни
кратности k = 1 называются простыми корнями.
Каждый полином степени n имеет
n корней, в том числе и
кратных. Поэтому полином можно представить в виде произведения (факторизованная
форма)
, то λ является k – кратным корнем или
корнем кратности k многочлена
a(z). Корни
кратности k = 1 называются простыми корнями.
Каждый полином степени n имеет
n корней, в том числе и
кратных. Поэтому полином можно представить в виде произведения (факторизованная
форма)
![]()
![]() .
.
Пример 1. ![]() .
.
На рис.1 показан график этого полинома при вещественных z.
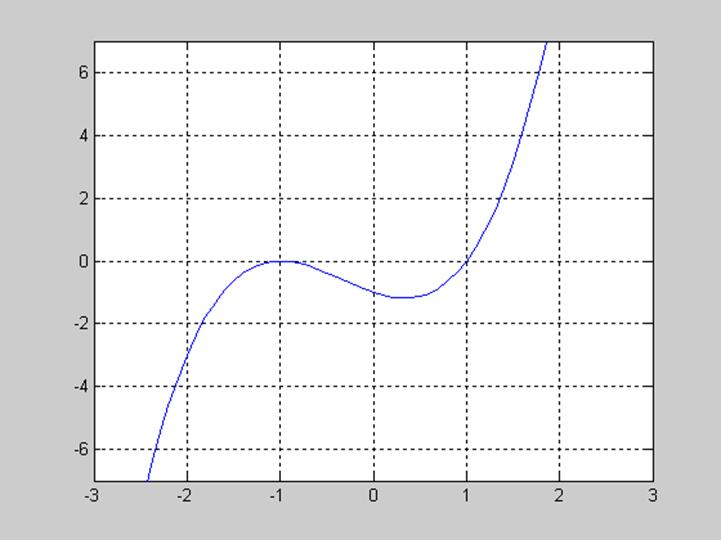
Рис.1
Число λ является k-кратным корнем полинома a(z), когда многочлен a(z) и его производные до порядка k
– 1 включительно обращаются в нуль при ![]() ,
а
,
а ![]() .
.
Если коэффициенты многочлена ![]() - действительные числа и λ –
корень полинома, т.е.
- действительные числа и λ –
корень полинома, т.е. ![]() , то для комплексно
сопряженного числа
, то для комплексно
сопряженного числа ![]() имеем
имеем ![]() , т.е.
, т.е. ![]() -
тоже корень a(z).
Поэтому для полиномов с действительными коэффициентами комплексные корни
всегда встречаются только комплексно сопряженными парами.
-
тоже корень a(z).
Поэтому для полиномов с действительными коэффициентами комплексные корни
всегда встречаются только комплексно сопряженными парами.
При действительных коэффициентах факторизованный вид полинома
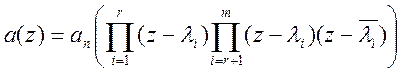 ,
,
где ![]() - действительные
корни
- действительные
корни
![]() - комплексные
корни.
- комплексные
корни.
Произведение ![]() представляет
собой квадратный полином с действительными коэффициентами.
представляет
собой квадратный полином с действительными коэффициентами.
Факторизованный полином 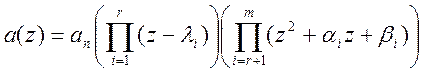 состоит
из полиномов первой и второй степени с действительными коэффициентами.
состоит
из полиномов первой и второй степени с действительными коэффициентами.
Пример 2. Полином ![]() имеет
корни
имеет
корни 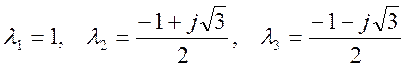 .
.
Факторизованная форма полинома ![]() ,
,
факторизованная форма полинома с действительными
коэффициентами ![]() .
.
Многочлен ![]() называется
устойчивым, если все его корни лежат в левой полуплоскости, т.е. если
все вещественные части корней - отрицательны.
Многочлены из примеров 1 и 2 относятся к неустойчивым. Легко доказать, что
многочлен первой или второй степени с вещественными коэффициентами и положительным
старшим коэффициентом an устойчив только тогда, когда все его коэффициенты
положительны. Для устойчивости многочленов более высоких степеней условие положительности
коэффициентов необходимо, но недостаточно.
называется
устойчивым, если все его корни лежат в левой полуплоскости, т.е. если
все вещественные части корней - отрицательны.
Многочлены из примеров 1 и 2 относятся к неустойчивым. Легко доказать, что
многочлен первой или второй степени с вещественными коэффициентами и положительным
старшим коэффициентом an устойчив только тогда, когда все его коэффициенты
положительны. Для устойчивости многочленов более высоких степеней условие положительности
коэффициентов необходимо, но недостаточно.
Составил: доц. Щетинин Ю.И.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.