Комплексные числа и алгебраические действия над ними
Рассмотрим квадратное
уравнение ![]() .
.
Определим его корни ![]() .
.
Не существует действительного
числа, квадрат которого равен -1. Но если формулой ![]() определить
оператор i как мнимую единицу, то решение этого уравнения можно записать
в виде
определить
оператор i как мнимую единицу, то решение этого уравнения можно записать
в виде ![]() . При этом
. При этом ![]() и
и
![]() - комплексные числа, в которых -1
это действительная часть, 2 или во втором случае -2 – мнимая часть. Мнимая
часть – это также действительное (вещественное) число. Мнимая часть,
умноженная на мнимую единицу, означает уже мнимое число.
- комплексные числа, в которых -1
это действительная часть, 2 или во втором случае -2 – мнимая часть. Мнимая
часть – это также действительное (вещественное) число. Мнимая часть,
умноженная на мнимую единицу, означает уже мнимое число.
В общем виде комплексное число имеет вид
z = x + iy ,
где x, y – вещественные
числа, ![]() – мнимая единица. В ряде прикладных
наук, например, в электротехнике, электронике, теории сигналов мнимая единица
обозначается через j. Вещественные числа x = Re{z} и y = Im{z} называются вещественной и мнимой частями числа
z. Выражение
– мнимая единица. В ряде прикладных
наук, например, в электротехнике, электронике, теории сигналов мнимая единица
обозначается через j. Вещественные числа x = Re{z} и y = Im{z} называются вещественной и мнимой частями числа
z. Выражение ![]() называется алгебраической
формой записи комплексного числа.
называется алгебраической
формой записи комплексного числа.
Любое
действительное число есть частный случай комплексного числа в виде ![]() . Мнимое число тоже частный случай
комплексного числа
. Мнимое число тоже частный случай
комплексного числа ![]() .
.
Определение множества комплексных чисел С
![]() .
.
Это выражение читается следующим
образом: множество С, состоящее из элементов ![]() ,
таких что x и y принадлежат множеству действительных
чисел R и
,
таких что x и y принадлежат множеству действительных
чисел R и ![]() - это мнимая единица. Отметим, что
- это мнимая единица. Отметим, что ![]() и т.д.
и т.д.
Два комплексных числа ![]() и
и ![]() равны, если и только если равны их
действительные и мнимые части, т.е.
равны, если и только если равны их
действительные и мнимые части, т.е. ![]() и
и ![]() .
.
Комплексные числа и функции широко используются в науке и технике, в частности, в механике, анализе и расчете цепей переменного тока, аналоговой электронике, в теории и обработке сигналов, в теории автоматического управления и др. прикладных науках.
Сложение двух комплексных чисел состоит в сложении их действительных и мнимых частей, т.е.
![]() .
.
Соответственно разность двух комплексных чисел
![]() .
.
Комплексное число ![]() называется
комплексно сопряженным числу z
= x + iy.
называется
комплексно сопряженным числу z
= x + iy.
Комплексно сопряженные числа z и z* отличаются знаками мнимой части. Очевидно, что
![]() .
.
Отсюда
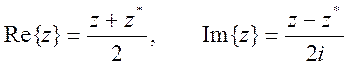 .
.
Любое равенство между комплексными выражениями остается
справедливым, если в этом равенстве всюду i заменить на -i,
т.е. перейти к равенству сопряженных чисел. Числа i и –i алгебраически
неразличимы, поскольку ![]() .
.
Произведение (умножение) двух комплексных чисел может быть вычислено следующим образом:
![]() .
.
Поэтому
![]() .
.
Деление двух комплексных чисел:
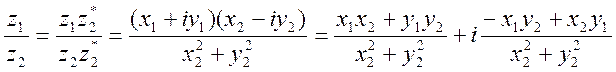 .
.
Пример:
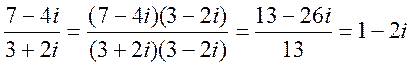 .
.
Комплексное число графически можно представить в прямоугольной системе координат. Зададим в плоскости прямоугольную систему координат (x, y).
На оси Ox будем располагать действительные части x , она называется действительной (вещественной) осью, на оси Oy –мнимые части y комплексных чисел. Она носит название мнимой оси. При этом каждому комплексному числу соответствует определенная точка плоскости, и такая плоскость называется комплексной плоскостью. Точке А комплексной плоскости будет соответствовать вектор ОА.
Число x называется абсциссой
комплексного числа ![]() , число y – ординатой.
, число y – ординатой.
Пара комплексно сопряженных чисел отображается точками, расположенными симметрично относительно действительной оси.
 |
Если на плоскости задать полярную
систему координат, то каждое комплексное число z определяется полярными координатами ![]() . При этом модуль числа
. При этом модуль числа ![]() – это полярный радиус точки, а угол
– это полярный радиус точки, а угол
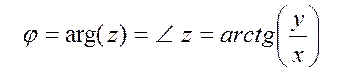 - её полярный угол
или аргумент комплексного числа z.
- её полярный угол
или аргумент комплексного числа z.
Модуль
комплексного числа ![]() всегда неотрицательный. Аргумент комплексного числа не
определяется однозначно. Главное значение аргумента должно удовлетворять
условию
всегда неотрицательный. Аргумент комплексного числа не
определяется однозначно. Главное значение аргумента должно удовлетворять
условию ![]() . Каждой точке комплексной плоскости
соответствует также общее значение аргумента
. Каждой точке комплексной плоскости
соответствует также общее значение аргумента ![]() .
Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент
числа нуль не определен.
.
Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент
числа нуль не определен.
Главное значение аргумента определяют по выражениям:
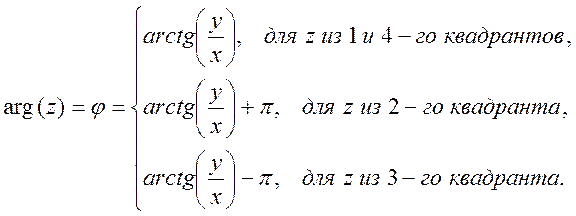
Очевидно, что ![]()
При этом
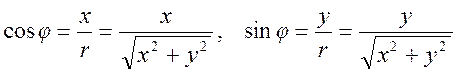 ,
, 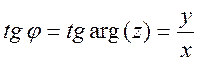 .
.
Представление комплексного числа z в виде
![]()
называется тригонометрической формой комплексного числа.
Пример.
![]()
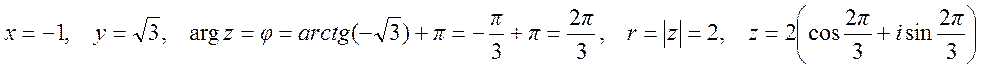
Разложение в ряд Маклорена
для функций действительного аргумента ![]() имеет
вид:
имеет
вид:
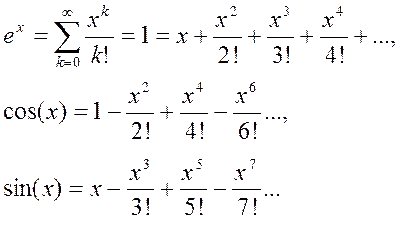
![]() Для экспоненциальной
функции комплексного аргумента z разложение имеет аналогичный характер
Для экспоненциальной
функции комплексного аргумента z разложение имеет аналогичный характер
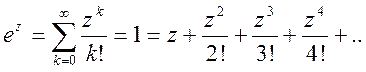 .
.
Разложение в ряд Маклорена для экспоненциальной функции мнимого аргумента можно представить как
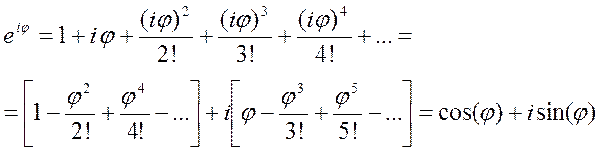
Получившееся тождество называется формулой Эйлера.
Для отрицательного аргумента ![]() оно
имеет вид
оно
имеет вид
![]() .
.
Комбинируя эти выражения, можно определить следующие выражения для синуса и косинуса
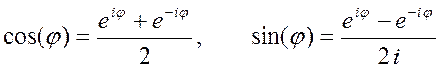 .
.
Пользуясь формулой Эйлера, из тригонометрической формы представления комплексных чисел
![]()
можно получить показательную (экспоненциальную, полярную) форму комплексного числа, т.е. его представление в виде
![]() ,
,
где ![]() - полярные
координаты точки с прямоугольными координатами (x,y).
- полярные
координаты точки с прямоугольными координатами (x,y).
Число, сопряженное
комплексному числу ![]() , в показательной форме записывается
следующим образом
, в показательной форме записывается
следующим образом ![]() .
.
Для показательной формы легко определить следующие формулы умножения и деления комплексных чисел
![]() ,
, ![]()
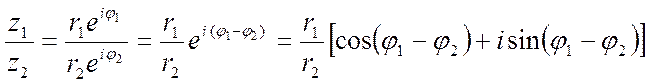 ,
,
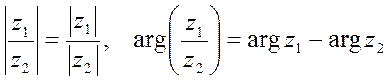
Т.е., в показательной форме произведение и деление комплексных чисел выполняется проще, чем в алгебраической форме. При умножении модули сомножителей перемножаются, а аргументы складываются. Это правило распространяется на любое число сомножителей. В частности, при умножении комплексного числа z на i вектор z поворачивается против часовой стрелки на 90
При делении модуль числителя делится на модуль знаменателя, и из аргумента числителя вычитается аргумент знаменателя.
Используя показательную форму комплексных чисел, можно получить выражения для известных тригонометрических тождеств. Например, из тождества
![]()
с помощью формулы Эйлера можно записать
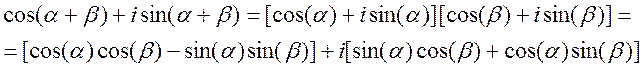
Приравнивая действительную и мнимую части в данном выражении, получаем выражения для косинуса и синуса суммы углов
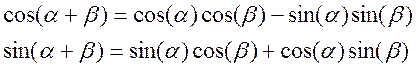
Возведение комплексного числа
![]() в натуральную степень n производится
по формуле
в натуральную степень n производится
по формуле
![]() ,
т.е.,
,
т.е.,
![]()
![]() .
.
Пример. Вычислим ![]() .
.
Представим число ![]() в тригонометрической форме
в тригонометрической форме
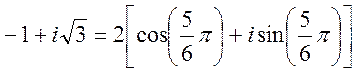 ’
’
Применяя формулу возведения в степень, получим
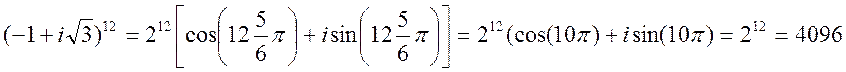 .
.
Положив в выражении ![]() значение r = 1, получим так называемую формулу Муавра
значение r = 1, получим так называемую формулу Муавра ![]() , при помощи которой можно
определять выражения синусов и косинусов кратных углов.
, при помощи которой можно
определять выражения синусов и косинусов кратных углов.
Корень n–й степени из комплексного числа z имеет n различных значений, определяемых по выражению
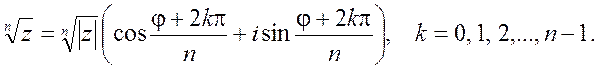
Пример. Найдем ![]() .
.
Для этого выразим комплексное
число (![]() ) к тригонометрической форме
) к тригонометрической форме
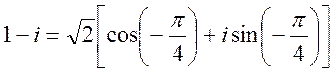 .
.
По формуле вычисления корня из комплексного числа, получаем
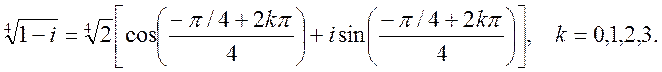
Логарифм комплексного числа z – это число w, для которого ![]() .
Натуральный логарифм комплексного числа имеет бесконечное множество значений и
вычисляется по формуле
.
Натуральный логарифм комплексного числа имеет бесконечное множество значений и
вычисляется по формуле
![]()
При этом ln(r)– обычный вещественный логарифм модуля r.
Пример.
![]() .
.
Справедливо равенство ![]() .
.
В
электротехнике, электронике, обработке сигналов и др. областях часто используются
функции, для которых независимая переменная вещественная, но функция принимает
комплексные значения, например, а) ![]() , б)
, б) ![]() .
.
Подобную функцию можно разложить на вещественную и мнимую части, например,
![]() Таким
образом, комплексная функция от вещественного аргумента представляется двумя
вещественными функциями того же аргумента. Например, комплексное напряжение
Таким
образом, комплексная функция от вещественного аргумента представляется двумя
вещественными функциями того же аргумента. Например, комплексное напряжение
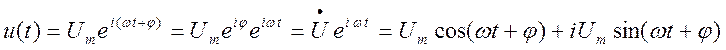 состоит
из действительной (косинусоидальной) и мнимой (синусоидальной) части. Такое
напряжение можно представлять как вектор длиной Um , начальной фазой (углом)
состоит
из действительной (косинусоидальной) и мнимой (синусоидальной) части. Такое
напряжение можно представлять как вектор длиной Um , начальной фазой (углом) ![]() ,
вращающийся с угловой скоростью ω.
,
вращающийся с угловой скоростью ω.
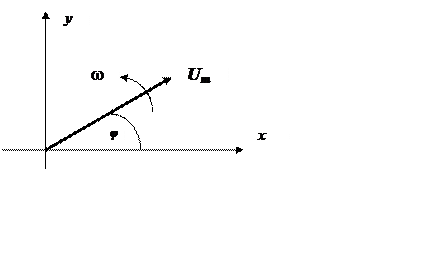
При этом если комплексные функции складываются, то складываются их вещественные и мнимые части. Если комплексная функция умножается на константу или вещественную функцию, то её вещественная и мнимая части умножаются на тот же множитель. Дифференцирование / интегрирование такой комплексной функции сводится к дифференцированию / интегрированию вещественной и мнимой части.
Например, дифференцирование выражения комплексного напряжения
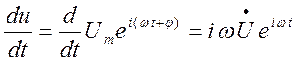 заключается
в умножении его на iω.
заключается
в умножении его на iω.
Поэтому проще и быстрее выполнять все вычисления над всей комплексной функцией, а в качестве окончательного выражения взять вещественную или мнимую часть от результата.
Пусть Е
– множество точек в плоскости ![]() , а G - множество точек в плоскости
, а G - множество точек в плоскости ![]() . На множестве Е задана
функция комплексного переменного
. На множестве Е задана
функция комплексного переменного ![]() , если каждому
числу
, если каждому
числу ![]() по некоторому правилу поставлено в
соответствие единственное число
по некоторому правилу поставлено в
соответствие единственное число ![]() . Функцию f(z)_
можно записать в виде
. Функцию f(z)_
можно записать в виде ![]() , где
, где ![]() - вещественная часть функции f(z),
а
- вещественная часть функции f(z),
а ![]() – мнимая часть функции. Примеры:
– мнимая часть функции. Примеры: 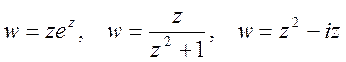 .
.
Значение z изображается точкой в комплексной плоскости z, а соответствующее значение w - точкой в комплексной плоскости w. При отображении w = f(z) линии плоскости z переходят в линии плоскости w, фигуры одной плоскости в фигуры другой, но формы линий или фигур могут существенно измениться.
Упражнения:
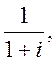 б)
б)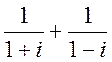 , в)
, в) 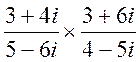 .
.Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.