Электрический ток. Закон Ома. Разветвленные цепи. Правила Кирхгофа. Закон Джоуля-Ленца. О зонной теории, страница 9

В дальнейшем будем предполагать, что в пространстве находятся только линейные магнетики. В этом случае затраченная работа идет на увеличение потенциальной энергии взаимодействия токов. Таким образом   .

С помощью формулы (6) представим последнее соотношение в виде    .(8)

Магнитная энергия не должна зависеть от последовательности включения токов (другая альтернатива противоречит постулатам термодинамики – можно создать вечный двигатель первого или второго рода). Поэтому, сумма в (8) должна сворачиваться в полный дифференциал. Это возможно, если матрица коэффициентов  является симметричной:  (данное свойство называется теоремой взаимности). Воспользуемся этим обстоятельством, чтобы преобразовать (8) к виду

После интегрирования получаем

 .(9)

Потенциальную энергию магнитного взаимодействия токов можно выразить в разных формах. Одна из них в случае объемных токов выглядит как  .

Другое выражение для энергии получим на примере длинного соленоида. Поле соленоида  .

Магнитный поток через соленоид   .

Потенциальная энергия тока в соленоиде длиной l согласно (9) равна    .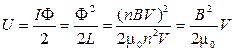

Можно сказать, что энергия локализована в магнитном поле с объемной плотностью 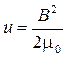  .(10)

Существование электромагнитных волн и перенос ими энергии подтверждают данное заключение. Формула (10) справедлива и в общем случае произвольных токов и переменных полей.

Вопрос №37:

Переходные процессы в цепи с индуктивностью. При изменении тока согласно закону электромагнитной индукции в индуктивности возникает ЭДС самоиндукции

 .
Знак минус показывает, что e препятствует изменению силы тока, т.е. в явлениях самоиндукции ток обладает своего рода инерцией.

Будем рассматривать квазистационарные токи. В этом случае мгновенные значения токов и полей такие же, как и в стационарном режиме и для расчета цепей можно применять законы постоянного тока. Рассмотрим процесс включения и выключения тока, предполагая его квазистационарным. При наличии в цепи индуктивности установление тока происходит не мгновенно, а постепенно.

Замыкание цепи. В момент времени t=0 замкнем цепь (рис.). Согласно закону Ома  .

Решение этого дифференциального уравнения с учетом начального условия  имеет вид

 , где  представляет собой установившийся ток (при ),  – постоянная времени, которая имеет размерность времени и определяет быстроту установления тока. График зависимости  – возрастания силы тока со временем показан на рис. (кривая 1).

Размыкание цепи. Первоначально к цепи подключена внешняя ЭДС и в цепи течет постоянный ток  (сопротивления источника ЭДС e и индуктивности L считаем пренебрежимо малыми). В момент времени t=0 быстро произведем переключение как указано на рис. При этом сохраняется замкнутость цепи, содержащей сопротивление и индуктивность. Для этой цепи согласно закону Ома

 .
Решение этого уравнения с учетом начального условия  имеет вид  ,где  – постоянная времени (время релаксации), которая характеризует скорость убывания тока. На рис. показан график зависимости  – убывания силы тока со временем (кривая 2).

Вопрос №38:

Цепи переменного тока. Рассмотрим линейную цепь с емкостью, индуктивнос­тью, сопротивлением и источником ЭДС. Получим закон Ома для данной цепи (раньше рассматривались частные случаи). С этой целью запишем законы Ома для отдельных элементов, считая их идеальными:

Для сопротивления: ;

для источника ЭДС:     ;

для индуктивности:           ;

для емкости:        .

В каждом уравнении  есть падение потенциала на соответствующем элементе. Сложив эти уравнения, получим

 ,(1)

где для убыли потенциала во всей цепи () использовано обозначение U. Это уравнение можно рассматривать как закон Ома для квазистационарных токов.

Уравнение (1) целесообразно продифференцировать по времени и записать результат в виде

 ,                                                                       (2)

Рассмотрим цепь, в которой ЭДС источников меняются по гармоническому закону. Для ее расчета удобно пользоваться комплексной формой для всех изменяющихся величин. Так как все сторонние ЭДС изменяются по закону

,то, очевидно, что падение потенциала и сила тока в каждой ветви также должны изменяться со временем по закону

 ,    причем , ,  являются комплексными величинами. Поэтому уравнение (2) принимает вид

 .

Разделив обе части уравнения на iw, представим его в виде

 (3)

где  называется импедансом. Уравнение (3) имеет вид закона Ома, в который входит импеданс. Для переменного тока импеданс играет роль сопротивления и учитывает не только соотношение между амплитудами силы тока и напряжения, но соотношения между их фазами.

Правила Кирхгофа для постоянного тока легко обобщаются на переменные токи без изменения их вида:

1) в каждом узле   (4а)

2) для всякого замкнутого контура   (4б)

Решение уравнений (4а) и (4б) позволяет найти как амплитуды, так и фазы всех сил токов.

Сопротивления: индуктивное wL и емкостное 1/(wC).

Вопрос №39:

Резонанс напряжений. Рассмотрим цепь, в которую последовательно с генератором включены R, L, C (рис). На основании  амплитуда тока  и разность фаз j между током и внешним напряжением

 ,  .

Сила тока достигает максимума при частоте  ,

которая называется резонансной частотой контура. При этом амплитуда силы тока равна , а разность фаз j = 0. Векторная диаграмма напряжений изображена на рис. В боль­шинстве случаев в резонансе омическое сопротивление R много меньше индуктивного wL (и емкостного 1/(wC)). Поэтому напряжение на индуктивности (и емкости) много больше внешнего, и на этом основании резонанс называют резонансом напряжений.

Резонанс токов. Рассмотрим цепь, изображенную на рис. Сила тока в цепи равна 

В большинстве практически важных случаев  и поэтому

 .

Следовательно, при частоте  

цепь ведет себя как чисто омическое сопротивление, импеданс цепи достигает максимума, а сила тока – минимума. Однако силы тока  и  при этом не являются минимальными. Внутри контура циркулируют очень большие токи по сравнению с током во внешней цепи. Поэтому сам резонанс называется резонансом токов. Векторная диаграмма токов изображена на рис.