Электрический ток. Закон Ома. Разветвленные цепи. Правила Кирхгофа. Закон Джоуля-Ленца. О зонной теории, страница 11

Исключение составляет случай, когда все пространство заполнено однородным изотропным магнетиком.. Рассмотрим случай объемных токов проводимости.

В магнетике, помещенном в магнитном поле, возникают токи намагничивания  .

Так как магнетик заполняет все пространство, то поверхностные токи намагничивания отсутствуют. Таким образом, конфигурация токов намагничивания и токов проводимости совпадают. Результирующий ток будет пропорционален току проводимости  .

Следовательно, индукция результирующего поля B пропорционально индукции магнитного поля в отсутствии магнетика    .(5)

Магнитное поле при заполнении пространства однородным магнетиком возрастает в m раз.

Если разделить (5) на , то получим  (6) – в рассматриваемом случае поле H оказывается таким же, как и в вакууме.

Вопрос №43:

Уравнения Максвелла.

При релятивистском обобщении закона Кулона были получены осново­полагающие законы электромагнетизма – уравнения Максвелла и выражение для силы Лоренца. Инвариантность уравнений Максвелла относительно преобразований Лоренца обусловливается в этом случае их формой и соотношением , которое постулируется как точное.

Воспроизведем основные моменты наших рассуждений. Законы электростатики (закон Кулона и принцип суперпозиции) в полевой форме выражаются уравнениями

 ,(1)   ,(2)   .(3)

Причем, в системе неподвижных зарядов сила, действующая на заряд q, не зависит от его скорости, что обусловлено (насколько известно в настоящее время) отсутствием в природе магнитных зарядов.

Теория относительности устанавливает, что силу, действующую на заряд q со стороны равномерно движущегося заряда (зарядов), можно представить в виде  .(4)

В свою очередь, для векторов E и B теория определяет уравнения

 ,(5)   ,(6)   ,(7)

,(8)
На следующем шаге уравнения (4)-(8) обобщались на случай произвольно движущихся зарядов. В сочетании с принципом суперпозиции уравнения (4)-(8) приобретают общий характер. Причем под r и j понимается суммарные плотность заряда и плотность тока.

Система (5)-(8), при известном движении зарядов (известных r и j), полная: ее решение однозначно при заданных граничных и начальных условиях.

Из уравнения (8) следует, что помимо электрического тока источником магнитного поля является переменное электрическое поле. Величину  Максвелл назвал током (точнее, плотностью тока) смещения, а сумму  – полным током. Открытие Максвеллом этого явления (тока смещения) аналогично открытию электромагнитной индукции. В отличие от последней оно чисто теоре­тическое открытие.

Уравнения (5)-(8) являются уравнениями электромагнитного поля в вакууме.В среде уравнения Максвелла приобретают вид

 ,(5а)   ,(6а)   ,(7а)

 .(8а)

В отличие от уравнений (5)–(8) система (5а)–(8а) уже не является полной – ее недостаточно для нахождения полей по заданному распределению зарядов и токов. Эти уравнения дополняются так называемыми материальными уравнениями.

,   ,

где e, m – постоянные, характеризующие электрические и магнитные свойства среды (диэлектрическая и магнитная проницаемости).

Если пространство заполняет несколько разных сред, то на их границах выполняются следующие граничные условия

 .                                   (7)
Здесь первое и последнее условия относятся к случаям, когда на границе раздела нет ни сторонних зарядов, ни токов проводимости.

Вопрос №44:

Закон сохранения энергии электромагнитного поля. Поток энергии. При изучении статических полей и постоянных токов были получены формулы для энергии поля и работы, совершаемой ими при изменении конфигурации зарядов и токов.

Рассмотрим некоторый замкнутый объем V, в котором имеются электро­магнитные поля и токи. Мощность, развиваемая действующими на ток силами, равна   (8)

Все силы неэлектрического происхождения характеризуются здесь напряженностью поля сторонних сил . В обобщенной форме эта напряженность описывает сопротивление среды протеканию тока, сторонние ЭДС и т.п. Работа всех сил идет на увеличение кинетической энергии носителей заряда. Выделим в соотношении (8) работу, совершаемую силами электромагнитного поля  (9)

Подставляя в (9) выражение для j из уравнения (8а), получаем

.

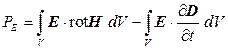По формуле векторного анализа

 имеем

 ,
где использовано соотношение (6а). Учитывая, что в случае линейной среды    и    ,

и преобразуя поверхностный интеграл по теореме Гаусса-Остроградского в интеграл по поверхности S, ограничивающей объем V 

Рассматривая поле как носитель энергии, заключаем, что величина

характеризует плотность электромагнитной энергии, а величина

, которая называется вектором Пойтинга, является плотностью потока энергии.

Строго говоря, для обеих величин, u и S, из уравнений Максвелла нельзя получить однозначных выражений; приведенные выражения являются простейшими из бесконечного числа возможных. Поэтому эти соотношения следует рассматривать как постулаты, справедливость которых подтверждается согласием выводимых из них следствий с опытом.

Вопрос №45:

Электромагнитные волны. Из уравнений Максвелла следует существование электромагнитных волн.   

 (3)  .(4)

Уравнения (3) и (4) представляют собой волновые (векторные) уравнения. Частные решения этих уравнений имеют вид

,    ,(5)

где правые части уравнений (5) есть некоторые векторные функции одного аргумента, а n – единичный вектор.

Смысл этих решений прост. Функции (5) представляют собой волну, движущуюся в направлении вектора n со скоростью c. Волны вида (5) называются плоскими волнами.

Если вектора волны меняются по гармоническому закону

 ,    ,                                            (6)
то такая волна называется гармонической или плоской монохроматической. Очевидно, что модуль вектора k, называемого волновым вектором, равен  .

Длина волны l - это расстояние, на которое точка постоянной фазы перемещается за один период колебаний  .