Цепи с обратной связью. Нелинейные цепи. Усилительные устройства. Автоколебательные системы (12-15 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева)

достигает наибольшего значения. На этой частоте в резонаторе возбуждается наиболее простое по структуре электромагнитное; поле, а сам он имеет минимальные габариты. Кроме того, основ­ная резонансная частота наиболее удалена от нежелательных высших типов колебаний. Более сложные типы колебаний иногда применяются для получения очень высокой добротности резонатора.

              Резонансная частота зависит от размеров резонатора, электро­магнитных параметров ε и μ заполняющей среды и структуры элек­тромагнитного поля. Отсюда следуют способы перестройки резо­нансной частоты резонатора, которую можно осуществлять изме­нением линейных размеров резонатора (чаще всего его длины), его объема (уменьшая его размещением в резонансной полости металлических тел) либо изменением параметров заполняющей диэлектрической среды (внося в резонансный объем диэлектри­ческое тело с другими параметрами ε и μ).

              Добротность резонатора тем больше, чем выше удельная про­водимость материала стенок и чем меньше ток в стенках, т.е. чем меньше напряженность магнитного поля у стенок резонатора. Рас­пределение напряженности магнитного поля в объеме резонатора определяется типом и порядком колебаний, поэтому и доброт­ность имеет различные значения для отличающихся по структуре полей.

             На собственную добротность объемного резонатора значитель­ное влияние оказывает качество внутренней поверхности оболоч­ки. Для уменьшения потерь внутреннюю поверхность резонатора тщательно полируют и покрывают слоем серебра (или золота для дополнительного придания коррозионной стойкости), а швы и соединения располагают параллельно линиям тока на стенках.

              В первом приближении собственная добротность Q₀резонато­ра пропорциональна отношению его объема к площади его пол­ной поверхности и обратно пропорциональна толщине скин-слоя проводника стенок. Такая зависимость объясняется тем, что энер­гия, накапливаемая в резонаторе, пропорциональна его объему, а тепловые потери энергии зависят от проводящих свойств мате­риала и общей поверхности стенок резонатора, по которым про­текают токи проводимости.

              Резонансное сопротивление резонатора представляет собой со­противление между входными зажимами элемента связи. Оно оп­ределяется величиной собственных потерь и потерь, вносимых элементом связи. Максимального значения резонансное сопротив­ление достигает при расположении элемента связи, например штыря, в пучности напряженности электрического поля. В этом случае резонансное сопротивление полого резонатора может со­ставлять несколько МОм.

              При наличии потерь свободные электромагнитные колебания в резонаторе будут затухающими. Запасенная в нем энергия убывает со временем по экспоненциальному закону. Чем выше доб­ротность резонатора, тем дольше в нем продолжаются электро­магнитные колебания. При Q_экв= 100 и f₀= 1 ГГц начальный запас энергии в резонаторе уменьшится в 100 раз за 7,3 мкс. Значит, даже в высокодобротном резонаторе свободные колебания зату­хают очень быстро. Для компенсации потерь и поддержания неза­тухающих колебаний в резонаторы вводят энергию от внешних источников. В этом случае резонатор уже работает в режиме не свободных, а вынужденных колебаний.

             При подключении к резонатору внешнего источника энергии в первый момент в нем возбуждаются свободные колебания на резонансной частоте и вынужденные колебания на частоте источ­ника. Однако вследствие потерь свободные колебания быстро за­тухают, а вынужденные колебания продолжаются, поддерживае­мые энергией источника. Время установления стационарного режи­ма колебаний в резонаторе пропорционально отношению (Q_экв/ω₀).

             Одним из наиболее простых типов объемных резонаторов, широко используемых в устройствах СВЧ, являются резонаторы на отрезках металлических волноводов, ограниченные с торцов металлическими стенками. На рис. 11.12 показаны различные типы закрытых волноводных резонаторов: прямоугольный, цилиндри­ческий и коаксиальный.

              В бесконечном полом металлическом волноводе поле в попе­речной плоскости имеет характер стоячей волны, а в продольном направлении представляет бегущую волну с длиной λ_в. При этом для прямоугольного волновода в плоскости поперечного сечения в стоячей волне между противоположными стенками волновода должно укладываться целое число полуволн. Если ограничить от­резок волновода длиною l в продольном направлении двумя по­перечными металлическими плоскостями, то поле в этом направ­лении в образованном резонаторе будет существовать только в виде стоячей волны. Такая возможность реализуется только на часто­тах, для которых на длине резонатора l укладывается целое число

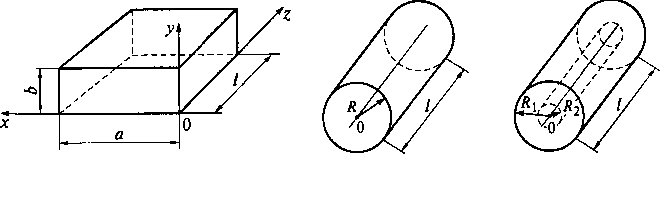
а                                       б                                 в

Рис. 11.12. Типы закрытых волноводных резонаторов:

а — прямоугольный; б — цилиндрический; в — коаксиальный

рполуволн поля бегущей волны, существующей в соответствую­щем волноводе. Таким образом, длина объемного резонатора дол­жна удовлетворять условию l = рλ_в/2, где р = 0, 1, 2, 3, ... . Заме­няя значение λ_в выражением (10.5) и решая полученное уравне­ние относительно λ, находим резонансную длину резонатора:

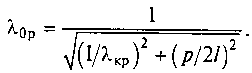                                                                                   (11.1)

                В выражении (11.1) параметр р равен нулю только для волн Е-типа. В этом случае λ₀= λ_кр, т.е. резонансная длина волны соответ­ствует критической длине E-волны в волноводе. Но при этом из (10.5) получается, что λ_в →∞. Таким образом, длина резонатора для волн E-типа при λ₀= λ_кр не определена и может быть произ­вольной. Вариации поля вдоль длины резонатора в этом случае отсутствуют, а резонансная длина волны и частота зависят только от поперечных размеров резонатора. Причиной таких свойств волн E-типа в объемном резонаторе является отсутствие в их структуре при λ₀= λ_кр поперечных компонентов электрического поля.

              Для волн T-типа критическая длина волны стремится к беско­нечности и выражение (11.1) для резонансной длины волны уп­рощается:

                                                                                                       (11.2)

где р = 1, 2, 3, ... .

              Прямоугольный резонатор можно рассматривать как отрезок прямоугольного волновода, замкнутый с обоих концов стенками (см. рис. 11.12, а). Если длина такого отрезка оказывается кратной полуволне, то вдоль нее могут возникнуть стоячие волны, т.е. мо­гут проявляться резонансные явления.

              Структура резонансных полей в резонаторе в плоскости, попе­речной его длине, имеет тот же вид, что и в бегущей волне в соответствующем прямоугольном волноводе. Поэтому колебания в резонаторе обозначаются по аналогии с типами и порядком волн в волноводе, т.е. Е_тпр и Н_тпр. Целые числа т, п и р указывают число полуволн, укладывающихся вдоль размеров соответственно а, bи l. Выражение для резонансной длины волны прямоугольно­го резонатора получим, подставив значение λ_кр из (10.3) в (11.1):