Цепи с обратной связью. Нелинейные цепи. Усилительные устройства. Автоколебательные системы (12-15 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 12

               Приложение бесконечно медленно изменяющегося напряже­ния (например, между эмиттером и коллектором) и постоянного напряжения между базой и эмиттером биполярного транзистора позволяет получить ВАХ нелинейного сопротивления между кол­лектором и эмиттером данного транзистора. Эта ВАХ будет пред­ставлять собой ВАХ двухэлектродного прибора. При дискретном изменении напряжения между базой и эмиттером биполярного транзистора можно получить множество ВАХ двухэлектродных приборов. На рис. 13.4 приведены выходные и проходные ВАХ би­полярного транзистора, а на рис, 13.4, б — соответственно для i_к = f(u_кэ)|_i6=const  и i₆= f(u_бэ)| u_{кэ =const} , а на pис. 13.5 приведены выходные и передаточные ВАХ полевого транзистора соответствен­но для

 i_c=f(u_си)| _uзи=const и i_c=f(u_зи)| _uси=const  этого транзистора.

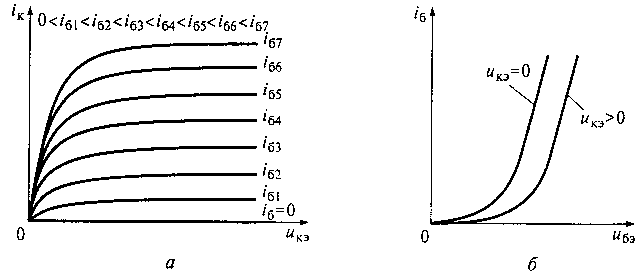
Рис.  13.4. Выходные (а) и входные (б) ВАХ биполярного транзистора

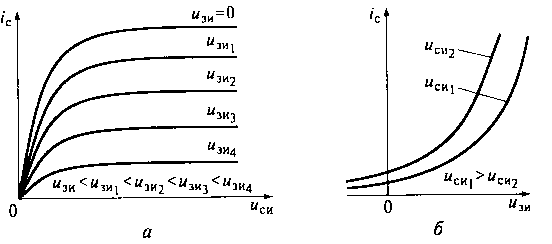
Рис. 13.5. Выходные (а) и проходные (б) ВАХ полевого транзистора

с управляющим р-п-переходом

               В соответствии с ВАХ нелинейных резисторов выделяют стати­стическое и дифференциальное сопротивления, определить кото­рые можно с помощью графика, приведенного на рис. 13.6.

              Статическое сопротивление характеризует сопротивление нели­нейного резистора в конкретной точке ВАХ этого резистора, на­пример точка А на рис. 13.6: R_ст= U₀/I₀= tgα, где U₀- постоянное напряжение, приложенное к нелинейному резистору; а I₀ — по­стоянный ток, протекающий через нелинейный резистор; α — угол между осью напряжений системы координат и прямой, проведен­ной через начало координат и точку А.

               Статические сопротивления нелинейных резисторов всегда имеют положительное значение.

               Дифференциальное сопротивление характеризует сопротивление нелинейного резистора при изменении напряжения и тока в ок­рестности заданной точки ВАХ. Прикладывая, например, к нели­нейному резистору в окрестности точки В его ВАХ (см. рис. 13.6) приращение напряжения Δu = u₂-u₁, получим соответствующее приращение тока

 Δi= i₂- i₁. В этом случае дифференциальное со­противление в точке В ВАХ нели­нейного резистора будет иметь вид R_ст = (Δu/Δi) = tgβ, где β — угол между касательной к точке В и осью напряжений системы ко­ординат. Устремляя к бесконечно малым величинам приращения напряжения Δuи тока Δi, т.е., переходя к пределу, получим выражение, позволяющее вычислить

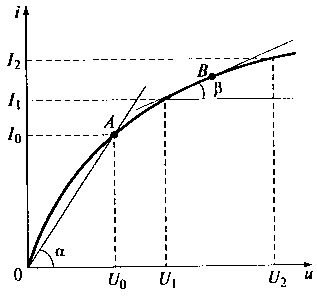
Рис. 13.6. Определение статического и дифференциального сопротивлений нелинейных резисторов

дифференциальное сопротивление нелинейного резистора, если известно, например, аналитическое описание его ВАХ: R_д =du/dt.

              Достаточно часто при анализе радиотехнических устройств ис­пользуют величину обратную дифференциальному сопротивлению. Эта величина называется дифференциальной крутизной нелиней­ного резистора: S_д= 1/R_д=di/du.

               Анализируя ВАХ нелинейных резисторов на рис. 13.4—13.6, отметим следующее. Вольт-амперные характеристики этих элемен­тов могут быть монотонно возрастающими di/du > 0 (входные и вы­ходные ВАХ транзисторов) либо иметь монотонно возрастающие участки (ВАХ туннельного диода и динистора). Для нелинейных резисторов, имеющих N-образные (туннельные диоды) и S-об­разные (динисторы) ВАХ элементов, характерно наличие участ­ков с монотонно убывающими ВАХ, для которых di/du < 0 (уча­стки а—б на рис. 13.2, б, в). Это участки с так называемым отрица­тельным дифференциальным сопротивлением.

               В нелинейных емкостных элементах заряд, накопленный в ем­кости, зависит от величины напряжения, приложенного к вне­шним выводам конденсатора. Емкость плоского (линейного) кон­денсатора определяется выражением: С= εε₀ S/d, где ε — диэлект­рическая проницаемость материала диэлектрика; ε₀ — диэлектри­ческая постоянная; S— площадь обкладок конденсатора; d — рас­стояние между обкладками конденсатора. В нелинейных емкостных элементах диэлектрическая проницаемость ε материала (например, сегнетоэлектроники) и расстояние между обкладками конденсато­ра d(например, обратносмещенный p-n-переход) зависят от при­ложенного к ним напряжения. Соответственно, емкости этих кон­денсаторов будут зависеть от приложенного к ним напряжения.

              Нелинейный емкостной элемент характеризуется статической и дифференциальной емкостями. Статическая емкость нелиней­ного конденсатора в конкретной точке его вольт-фарадной харак­теристики определяется как отношение заряда Q, накопленного в емкости, к напряжению и_cприложенному к внешним выводам конденсатора, т.е. С_cт= Q/u_c. Дифференциальная емкость определя­ется отношением накопленного заряда к приращению напряже­ния на емкости в окрестности какой-то точки его вольт-фарадной характеристики, т.е. С_д= dQ/du_c.

               Нелинейность ампер-веберных характеристик индуктивной ка­тушки, т.е. зависимость индуктивности от тока, протекающего через нее, возникает в индуктивных катушках с сердечниками из ферромагнитных материалов — сплавов железа и его оксидов (фер­риты). Нелинейность в подобных индуктивных катушках связана с нелинейной

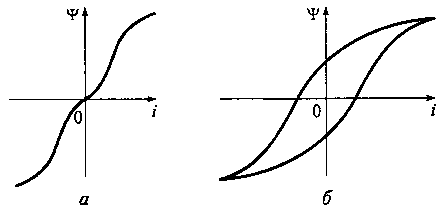
Рис. 13.7. Ампер-веберная характеристика нелинейной индуктивности (а)

и ее гистерезис (б)

зависимостью намагничивания материала сердечни­ка. На рис. 13.7 приведена типичная ампер-веберная характерис­тика нелинейной индуктивности и ее гистерезисный характер, возникающий при быстром перемагничивании сердечника индук­тивной катушки. Это приводит к потерям энергии в сердечнике.

                Нелинейная индуктивность характеризуется статической ин­дуктивностью

 L_ст = ψ/i и дифференциальной индуктивностью L_д = dψ/di, где ψ — потокосцепление в индуктивности.

13.2. Выбор рабочей точки нелинейного резистивного элемента

               Под рабочей точкой понимают значения постоянных напряже­ний на внешних выводах элемента и постоянных токов, протека­ющих через внешние выводы элемента, в статическом режиме.