Цепи с обратной связью. Нелинейные цепи. Усилительные устройства. Автоколебательные системы (12-15 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 14

13.3. Воздействие гармонического колебания на нелинейное сопротивление

               Нелинейная зависимость между током и напряжением в нели­нейном резисторе оказывает влияние на изменение формы сигна­лов, приложенных к этому элементу. Рассмотрим это на примере нелинейного резистора, ВАХ которого аппроксимируется поли­номом n-й степени:

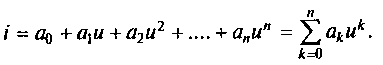                                                                    (13.1)

              Пусть к элементу приложено напряжение и = U_mcos(ωt), изме­няющееся по гармоническому закону. Подставляя это напряжение в (13,1), получим выражение, описывающее ток нелинейного резистора:

               Применив в полученном выражении к слагаемым со степеня­ми больше первой тригонометрические преобразования, получим их следующие представления:

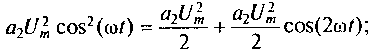
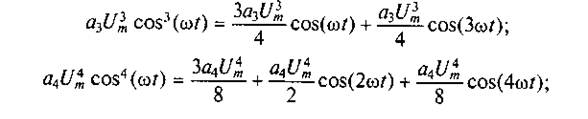
a₅U⁵_m cos⁵ (ωt)= (5a₅U⁵_m/8) cos (ωt)+(5 a₅U⁵_m/16) cos(3 ωt) +( a₅U⁵_m/16) cos(5 ωt).

              Тогда ток нелинейного резистора представится суммой спектраль­ных составляющих с частотами, кратными исходной частоте ω:

i= Iо + I₁ cos(ωt) + I₂cos(2 ωt) + I₃cos(3 ωt) + ...+ I_ncos(n ωt),

где Iо, I₁ I₂, ..., I_п— амплитуды гармонических составляющих, причем

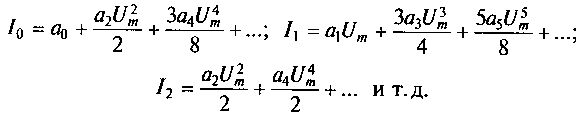
              Проведя анализ отклика (тока) нелинейного резистора при приложении к нему гармонического напряжения (входное воз­действие), отметим следующее:

              отклик представляет собой сумму спектральных составляющих с частотами, кратными частоте входного воздействия;

              в отклике присутствует постоянная составляющая I₀, которой нет во входном воздействии, при этом вклад в постоянную со­ставляющую отклика вносят только четные гармоники;

              номер максимальной гармонической составляющей равен сте­пени полинома, аппроксимирующего ВАХ нелинейного резистора;

              составляющие полинома с четными степенями соответствуют четным, а с нечетными степенями — нечетным гармоническим составляющим.

              Анализ отклика нелинейного резистора на входное воздействие, представляющее собой гармоническую функцию, показал, что в отклике присутствует множество гармонических составляющих с частотами, кратными частоте входного воздействия. Эта особен­ность нелинейных резисторов широко используется в радиотех­нических устройствах, например в умножителях частоты.

              Рассмотрим отклик нелинейного резистора при приложении к нему входного воздействия в виде суммы двух слагаемых, изменя­ющихся по гармоническому закону и имеющих разные частоты, u= U_ml cos ω₁ t +  U_m2 cos ω₂ t.

              Пусть нелинейный резистор аппроксимируется полиномом вто­рой степени i= a₀+ а₁ и + а₂ и². Подставив в полином входное воз­действие, получим ток нелинейного резистора

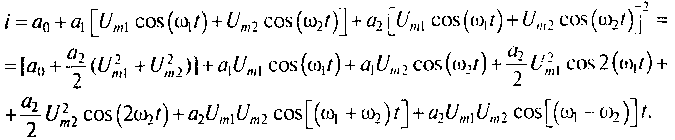
Анализируя приведенные вычисления, отметим следующее:

             в отклике присутствует постоянная составляющая [a₀ + (a₂ / 2) х (U_ml² + U_m2²)], которой нет во входном воздействии;

             в отклике присутствуют как гармонические составляющие с частотами ω₁ и ω₂ составляющих входного воздействия, так и с удвоенными частотами 2 ω₁ и 2 ω₂;

             в отклике присутствуют гармонические составляющие, соот­ветствующие сумме ω₁+ ω₂ и разности ω₁ - ω₂ частот составляю­щих входного воздействия;

             введение в полином, аппроксимирующий нелинейный резис­тор, слагаемого третьей степени а₃ u³приведет к появлению в спек­тре отклика как гармонических составляющих с утроенными час­тотами 3 ω₁ и З ω₂, так и гармонических составляющих с суммар­ными и разностными частотами (2 ω₁ + ω₂), (2 ω₁ - ω₂), (ω₁ + 2 ω₂) и (ω₁ - 2 ω₂). Присутствие в полиноме слагаемых более высоких по­рядков вызовет появление в отклике гармонических составляю­щих с более сложными суммарно-разностными частотами.

             Таким образом, при приложении к нелинейному резистору входного воздействия в виде суммы двух слагаемых, изменяющихся по гармоническому закону, но с разными частотами, можно по­лучить в отклике гармонические составляющие от суммы и разно­сти этих частот. Это свойство широко используется в радиотехни­ке, например при построении преобразователей частоты.

13.4. Воздействие гармонических колебаний на реактивный нелинейный элемент

              К реактивным нелинейным элементам относят нелинейную емкость и нелинейную индуктивность. На примере нелинейной емкости рассмотрим влияние нелинейности на процессы, проис­ходящие в цепи.

              Вольт-кулонная характеристика нелинейной емкости может быть описана, например, полиномом второй степени

q(u)= a₀+ а₁ и + а₂ и²,(13.2)

где a₀ = q₀ — заряд емкости в рабочей точке и =U₀; а₁ =dq(u)/du=C_д — дифференциальная емкость в рабочей точке; а₂ =(1/2)·(d²q(u)/du²)=(1/2)·(dC_д/du)- скорость изменения емкости в окрестности рабочей точки.

              Известно, что ток емкости характеризует скорость изменения заряда, т.е.

                                         i_c(t)=dq(u)/dt=( dq(u)/du)·(du/ dt ).                                     (13.3)

               Поэтому, подставляя (13.2) в (13.3), найдем ток нелинейной емкости

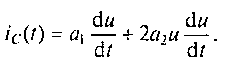                                                                           (13.4)

               Приложим к нелинейной емкости напряжение u(t) = U_mcos(ωt+φ), изменяющееся по гармоническому закону. В этом случае ток емкости согласно (13.4) будет иметь вид

i_c(t) = -a₁U _mωsin (ωt+φ)-а₂U_m²ωsin[2(ωt+φ)].

               Таким образом, в спектре тока нелинейной емкости, аппрок­симированной полиномом второй степени, присутствуют две гар­монические составляющие. Первая из них имеет амплитуду a₁U_mω и изменяется с частотой ω, а вторая имеет амплитуду а₂U_m²ω и изменяется с частотой 2ω. Если в полином (13.2) ввести слагае­мое третьей степени, то спектральная составляющая тока емко­сти, изменяющаяся с частотой ω, будет иметь амплитуду a₁U_mω + +0,75 a₃U_m³ ω. При этом появится спектральная составляющая, ам­плитудой 0,75 a₃U_m³ ω, изменяющаяся с частотой 3 ω.

               Из сказанного очевидно следующее: