Kу(Ů1,jω)=Ů2/ Ů1. (15.2)
На резонансной частоте контура коэффициент усиления нелинейного резонансного усилителя будет зависеть только от входного напряжения Kу(Ů1).
Четырехполюсник обратной связи имеет свой коэффициент передачи, зависящий от частоты:
(15.3)
Сравнивая выражения (15.2) и (15.3), можно определить, что в стационарном состоянии коэффициент усиления нелинейного резонансного усилителя Kу (Ů1,j ω A) и коэффициент передачи четырехполюсника обратной связи Kос(j ωА) являются комплексными величинами и имеют взаимообратные значения. Отсюда следует важное соотношение, характеризующее автогенератор:
(15.4)
где ω а — частота колебаний в автогенераторе.
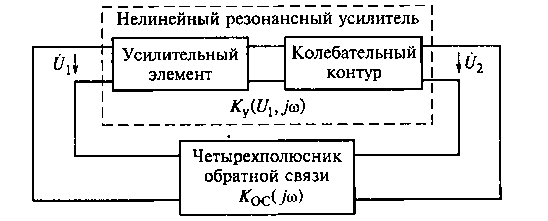
Рис. 15.1. Обобщенная структурная схема автогенератора
Комплексные коэффициенты
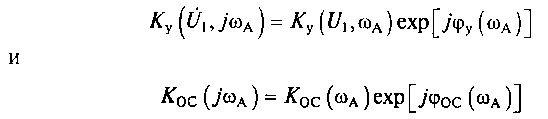
определяются модулем коэффициента усиления резонансного усилителя Kу (U1, ω А), модулем коэффициента передачи четырехполюсника обратной связи Kос(ω а), а также фазовыми сдвигами (аргументами), вносимыми резонансным усилителем φу(ωа) и четырехполюсником обратной связи φос(ω а).
С учетом вводимых параметров формула (15.4) преобразуется к виду
Выражение можно разбить на две части. Первая часть характеризует условие баланса амплитуд:
= 1, (15.5)
а вторая часть — условие баланса фаз в автогенераторе (15.6):
φу(ωа)+
где n = 1, 2, ... — любое целое число.
Только при выполнении условий баланса амплитуд (15.5) и фаз (15.6) в автогенераторе могут возникнуть незатухающие колебания.
Известно, что четырехполюсник обратной связи, как правило, состоит из пассивных элементов. В связи с этим его комплексный коэффициент передачи не зависит от приложенного напряжения, а определяется только параметрами элементов и частотой сигнала в цепи, поэтому на частоте ωа работы автогенератора модуль коэффициента передачи Koc(ωА) четырехполюсника обратной связи можно считать величиной постоянной. Учитывая это, в соответствии с выражением (15.5) модуль коэффициента усиления нелинейного резонансного усилителя можно представить в виде Kу(U1, ωA)= 1/Kос(ωА).
0UCTU1
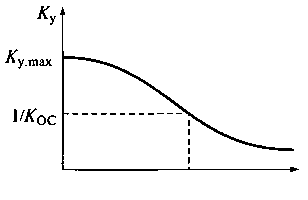
Рис. 15.2. Определение стационарного режима работы автогенератора
На рис. 15.2 показано графическое определение стационарного режима работы автогенератора. Модуль коэффициента усиления резонансного усилителя в зависимости от амплитуды входного напряжения U1 носит нелинейный характер. В результате этого в точке, в которой выполняется условие (15.5), достигается стационарная амплитуда выходного напряжения Uст автогенератора. Левее от этой точки произведение Kу(U1, ωA)Kос(ωА)превышает единицу, а правее становится меньше единицы. При выполнении равенства Kу(U1, ωA)= 1/Kос(ωА) достигается устойчивое равновесие в автогенераторе и в нем наблюдается незатухающий колебательный процесс.
Условие баланса фаз (15.6) говорит о том, что в стационарном режиме сдвиг фазы сигнала в кольце обратной связи автогенератора должен быть кратен 2π. В этом случае рост амплитуды выходного сигнала приводит к росту амплитуды входного сигнала резонансного усилителя (положительная обратная связь). При малом всплеске сигнала на входе усилительного элемента, например вследствие подключения напряжения питания к автогенератору, происходит выделение колебательным контуром спектральной составляющей на частоте ωа и ее усиление до достижения амплитуды Uст.
15.2. Физические процессы в автогенераторе
На рис. 15.3 приведена схема автогенератора с трансформаторной ОС. Используя эту схему, рассмотрим физические процессы, приводящие к возникновению колебаний в автогенераторе.
Для узла, в котором соединены между собой индуктивная катушка LK, конденсатор Ск, сопротивление потерь Rконтура и коллектор транзистора VT, в соответствии с первым законом Кирхгофа можно записать уравнение баланса токов iL+ iс+ iR= iк, где iL, iс,iR, iк — токи индуктивной катушки LK, конденсатора Ск, сопротивления потерь Rи коллектора транзистора VT.
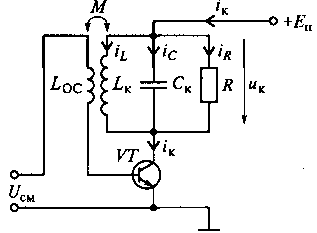
Рис. 15.3. Схема автогенератора с трансформаторной ОС
При напряжении на контуре uк(t) через элементы контура протекают токи
iL(t)=(1/Lk)∫t0uk(t)dt, ic(t)=Ck(duk(t)/dt) и iR(t)=uk(t)/R.
Ток коллектора iк транзистора зависит от напряжения uбэ- Uсм, приложенного между базой и эмиттером этого транзистора. За счет тока, протекающего через индуктивную катушку контура LK, и наличия взаимной индуктивности М между индуктивными катушками контура LK и цепи ОС Locв индуктивной катушке Locвозникает ЭДС обратной связи uoc(t).
Эта ЭДС является сигнальной составляющей напряжения, управляющего работой транзистора, так как uос=uбэ- Uсм. В результате этого ток коллектора iк транзистора становится зависимым от напряжения обратной связи иос.
Колебательный контур, включенный в коллектор транзистора VT, и индуктивная катушка обратной связи Loc образуют систему связанных контуров, в которой коэффициент связи определяется взаимной индуктивностью M. В связи с этим напряжение обратной связи можно представить в виде uос(t) = -(M/Lк)uк(t).
Переходной колебательный процесс в контуре описывается выражением (15.1), где ω св = ω 0 = 1/√(LkCk) — частота собственных колебаний в контуре. В этом случае коэффициент затухания имеет вид
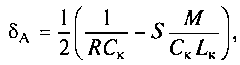(15.7)
где S=diK/duoc— дифференциальная крутизна транзистора, которая нелинейно зависит от напряжения обратной связи uос.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.