Сигналы и их детерминированные модели. Спектральное представление детерминированных сигналов (1, 2 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 9

Пример 2.2. Имеются две гармонические функции sin(ωt) и cos(ωt). Необходимо проверить ортогональность этих функций за период их из­менения Т = 2π/ω.

Решение. Используя выражение (2.7), вычислим взаимную энергию функций sin(ωt) и cos(ωt):

∫sin (ωt)cos(ωt)dt = ∫½sin(2ωt)dt =-¼ ω cos(2ωt)| =

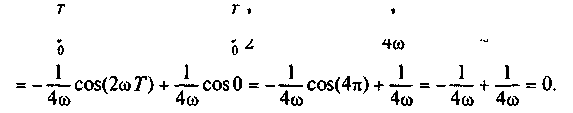
Видим, что взаимная энергия от двух гармонических функций равна нулю. Это доказывает их ортогональность.

Возможность использования той или иной системы ортонормированных функций при аппроксимации сложного периодичес­кого сигнала вытекает из тех целей, которые преследуются при аппроксимации. К числу этих целей относят:

наиболее точное представление периодического сигнала;

получение минимального числа членов обобщенного ряда Фу­рье при оговоренной точности аппроксимации.

При стремлении достичь точного представления сигнала наи­более часто используют ортонормированную систему гармоничес­ких функций sin(mωt) и cos(mωt). Это определяется следующими соображениями:

гармоническое колебание является простейшей функцией;

гармоническое колебание не поддается дальнейшему разложе­нию на спектральные составляющие;

гармонические колебания представляют собой функции вре­мени, которые единственные не изменяют своей формы при про­хождении через линейные радиотехнические цепи (элементы этой цепи имеют постоянные параметры), изменяются лишь амплиту­да и фаза колебания;

использование гармонических колебаний в качестве аппрокси­мирующих сигналов позволяет применять символические методы (например, метод комплексных амплитуд) для анализа линейных цепей в установившемся режиме.

При стремлении достичь приближенного разложения перио­дического сигнала широко используются системы ортонормированных функций типа полиномов (многочленов) Чебышева, Эрмита, Лагера или Лежандра.

Для примера следует отметить, что среднеквадратическая ошиб­ка аппроксимации прямоугольной разнополярной функции

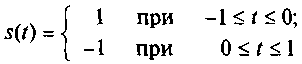
полиномом Лежандра с четырьмя членами ряда равна 28%, а три­гонометрическими функциями с четырьмя членами ряда 6,75 %.

Таким образом, представление сигнала тригонометрическимз рядом Фурье в сравнении с его представлением многочленом Лежандра обеспечивает в 4 раза более точный результат аппроксимации при одинаковом числе членов ряда. Учитывая это, основное внимание в учебнике будет уделено представлению сигналов гармоническими функциями.

2.3. Спектральное представление периодических сигналов

Допустим, имеется периодический сигнал сложной формы, пример одного из которых, отвечающий условию периодичности (2.1), показан на рис. 2.2. Опишем этот сигнал обобщенным рядом Фурье (2.6), используя в качестве ортогональной системы функций в интервале [-Т/2, Т/2] гармонические функции: η₀(t) = 1; η_1s(t) =

Все функции отвечают условию периодичности, а круговая частота ω₁ = 2π/Т определяется периодом T изменения сигнала.

Для аппроксимации сложного периодического сигнала обобщен­ным рядом Фурье (2.6) необходимо вычислить коэффициенты c_k по формуле (2.5). При этом учтем, что каждый коэффициент c_kопределяется суммой двух гармонических функций

 с одинаковыми круговыми частотами kω₁.

Заметим, что

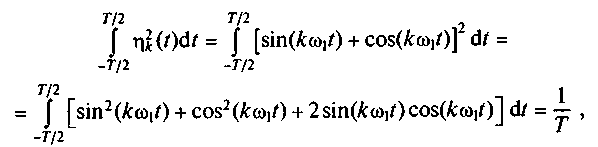
поскольку sin²(kω₁t) + cos²(kω₁t) = 1, а интеграл от произведет функций синус и косинус равен нулю.

Тогда выражение для расчета коэффициентов c_k принимает вид

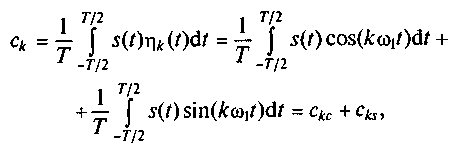(2.9)

где c_kc

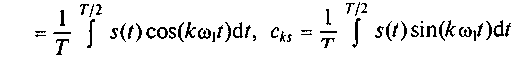
- косинусоидальная и синусоидальная составляющие коэффициентов Фурье.

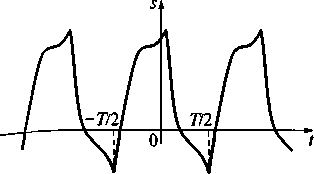
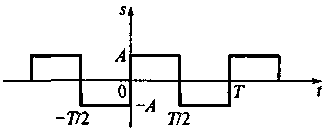
Рис. 2.2. Пример периодического сигнала сложной формы

Рис. 2.3. Пример периодического сигнала s(t), аппроксимируемогообобщенным рядом Фурье

Учитывая значения коэффициентов c_kcиc_ks, периодический сигнал описывается обобщенным рядом Фурье (2.6):

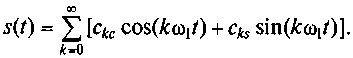
Проводя преобразования тригонометрических функций, это выражение можно представить в более наглядной форме:

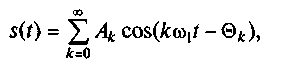(2.10)

где A_k =— амплитуда, а 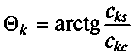 начальная фаза гармонической функции с круговой частотой kω₁

Пример 2.3. Необходимо аппроксимировать обобщенным рядом Фу­рье периодический сигнал s(t), показанный на рис. 2.3 и описываемый на временном интервале [—Т/2, Т/2] функцией

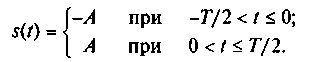
Решение. Для аппроксимации сигнала s(t) вычислим, используя выражение (2.9), коэффициенты c_k:

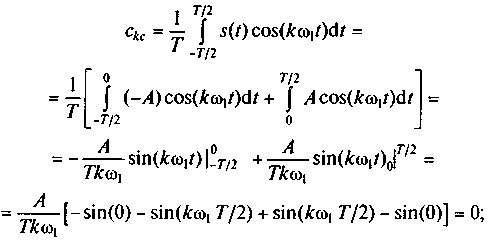
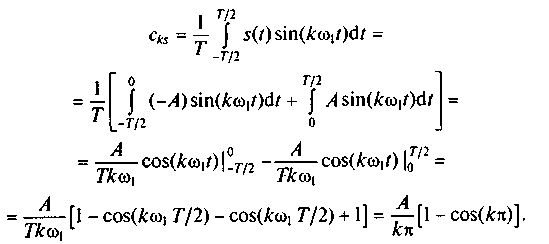
Используя значения коэффициентов c_kc и с_ks, найдем значения амплитуд A_k и начальной фазы  θ_k гармонических составляющих ряда Фурье (2.10):

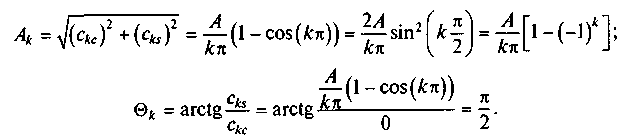
Таким образом, искомый сигнал (см. рис. 2.3) описывается следую­щим обобщенным рядом Фурье (2.10) в базисе гармонических функций:

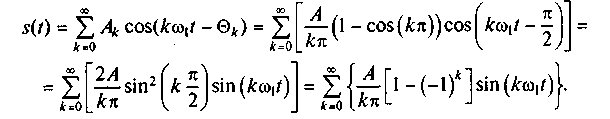
Вычислим первые шесть слагаемых ряда Фурье: при k = 0 с₀η₀(t) = 0; при k = 1 с₁η₁(t) = (2A/π)sin(ω₁t); при k = 2 с₂η₂(t) = 0; при k = 3 с₃η₃(t) = (2A/3π) )sin(3ω₁t); при k = 4 с₄η₄(t) = 0; при k = 5 с₅η₅(t) = (2A/5π) )sin(5ω₁t).

Расчеты показывают, что сигнал, представленный на рис. 2.3, аппроксимируется бесконечной суммой спектральных составляющих, каждая из которых изменяется с частотой, кратной частоте исходного колебания ω₁ = 2π/ Т. Эта кратность определяется рядом нечетных чисел k= 1, 3, 5, ... . Таким образом,

s(t) = 2A/π [sin(ω₁t) + 1/3sin(3ω₁t) + 1/5 sin(5ω₁t) + ... ]  .

Для записи обобщенного ряда Фурье (2.6) в тригонометрической форме можно использовать и другую систему ортогональных функций, например:

...ехр(-jkω₁t), ..., ехр(-j2ω₁t), ехр(-jω₁t), 1, ехр(jω₁t), ехр(j2ω₁t), ..., ехр(jkω₁t),… .(2.11)

Ортогональность функций (2.11) выполняется на временном интервале, равном периоду изменения Т = 2π/ω₁  исходного сиг­нала s(t).

В соответствии с системой ортогональных функций (2.11) обоб­щенный ряд Фурье (2.6) принимает вид

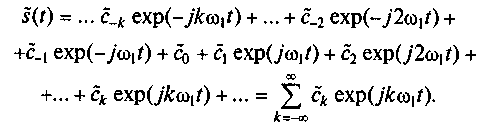(2. 12)

Коэффициенты обобщенного ряда Фурье рассчитываются по формуле

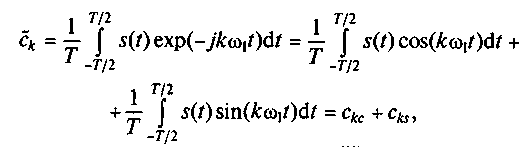
Комплексное число, описывающее коэффициент c_k в алгебраической форме (2.13), можно представить в показательной форме  c_k = |c_k| exp(jθ_k), где |c_k| = √(c_kc)² + (c_ks)² – модуль,

а θ_k =  -arctg (c_ks/ c_kc) - аргумент коэффициента c_k .

Тогда комплексная форма ряда Фурье (2.12) принимает вид