Сигналы и их детерминированные модели. Спектральное представление детерминированных сигналов (1, 2 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 6

Аналоговый сигнал s(t) можно представить в виде последова­тельности прямоугольных видеоимпульсов, следующих друг за дру­гом через равные временные интервалы Δt. На рис. 1.4. показана дискретизация аналогового сигнала при переменных амплитуде и длительности отсчетных импульсов.

В первом случае видеоимпульсы имеют одинаковую длитель­ность (см. рис. 1.4, а), а их амплитуды пропорциональны значени­ям исходного сигнала s(t) в отсчетных точках времени.

Во втором — все видеоимпульсы имеют одинаковые амплиту­ды (см. рис. 1.4, 6), а их длительность пропорциональна текущим временным отсчетам значений аналогового сигнала.

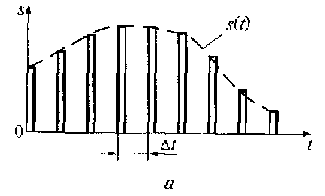
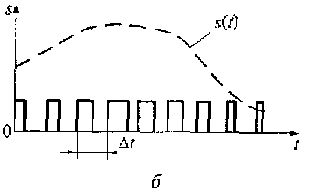
Рис. 1.4. Дискретизация аналогового сигнала при переменных амплитуде (а) к длительности (б) отсчётных импульсов.

1.3. Динамическое описание сигнала функцией включения и дельта-функцией

В радиотехнике и средствах связи отклик устройства ни произ­вольное входное воздействие в достаточно широком временном ди­апазоне представляется суммой элементарных сигналов, возника­ющих в последовательные моменты времени. Устремляя к нулю дли­тельность этих элементарных сигналов, в пределе получают точное представление о сигнале. Этот метод описания сигналов называется динамическим, что подчеркивает зависимость процесса от времени.

На рис. 1.5 показаны методы динамического описания сигна­лов на базе ступенчатых и импульсных функций. Оба метода на­шли широкое применение.

В первом методе в качестве элементарных сигналов использу­ются ступенчатые функции, возникающие через равные проме­жутки времени Δt (см. рис. 1.5, а). Высота каждой ступеньки равна приращению сигнала на интервале времени Δt, т.е. Δ Sj = Sj – S_{j - 1} , где j = 1, 2, ... . Во втором методе в качестве элементарных сигна­лов используются прямоугольные импульсы одинаковой длитель­ности Δt, но с высотой Sj, соответствующей аналоговому сигналу в момент времени t_j =jΔt, где j = 0, 1, 2 ... (см. рис. 1.5, б).

Для обоснования методов динамического представления сиг­налов рассмотрим функции, лежащие в их основе. К этим функ­циям относятся функция включения и дельта-функция (δ-функция). На рис. 1.6 показаны линейный закон передачи сигнала и график функции Хевисайда.

Функция включения (функция Хевисайда). Пусть задан сигнал (см. рис. 1.6, а), математическая модель которого описывается сле­дующим выражением:

U(t) = {0 при t < -ξ /2;  (1 + 2t/ ξ) /2 при - ξ /2 ≤ t ≤ ξ /2;  1  при  t > ξ /2.}

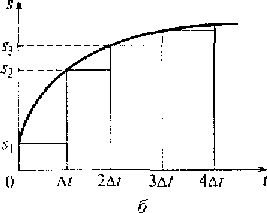
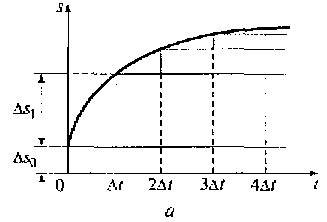
Рис.  1.5. Динамическое описание сигналов на базе ступенчатых (а) и импульсных (б) функций

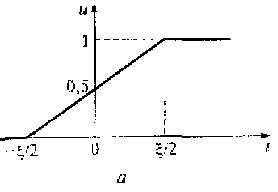
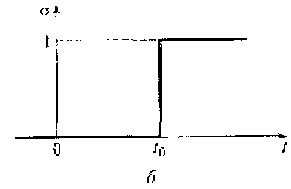
Рис. 1.6. Линейный закон передачи (а) и функция Хевисайда (б)

Эта функция отражает линейный закон перехода некоторого физического процесса из нулевого состояния в единичное состо­яние за время ξ. Математическая модель подобного перехода при стремящемся к нулю значении ξ получила название функции вклю­чения или функции Хевисайда:

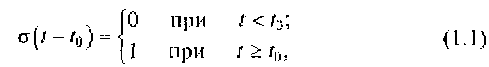
где t₀ — время, на которое функция включения смещена относи­тельно начала координат (см. рис. 1.6. б).

К числу основных свойств функции включения можно отнести следующие.

1.Функция включения позволяет получить аналитическое представление о поведении аналоговых сигналов s(t) до и после ком­мутации:

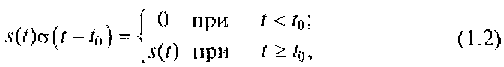
т.е. до и после того, как функция включения (1.1) приобретет единичное значение.

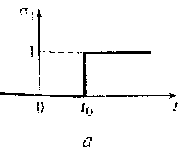
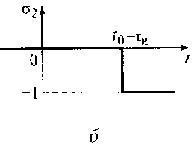
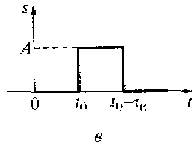
2. Разность σ(t) = σ₁(t) – σ₂(t) двух функций включения σ₁(t) = σ(t – t₀)   и  σ₂(t)= σ(t – t₀ – τ_и)     позволяет описать импульсный сигнал s(t)  с амплитудой А, длительностью τ_и и моментом появ­ления t₀. Формирование импульсного сигнала с использованием двух функций включения σ₁(t)  и  σ₂(t) показано на рис. 1.7:

s(t) = s₁(t) – s₂(t) =  A[σ₁(t) – σ₂(t)] =  A[σ(t - t₀) - σ(t - t₀ – τ_и)].(1.3)

Представление импульсных сигналов через функции включе­ния широко используется в радиотехнике.

Дельта-функция (функция Дирака). Рассмотрим импульсный сигнал

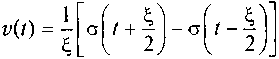
прямоугольной формы с амплитудой 1/ξ и длительностью ξ. В этом случае для описания импульса используется разность двух функций включения. На рис. 1.8 показаны прямоугольный импульс и символьное изображение дельта-функции.

∞ Пv =   ∫ vdt = 1         -∞

Заметим, что при любом параметре ξ площадь импульса с длительностью ξ, и амплитудой

1/ξ, равна единице, т.е.

И это несмотря на то, что при значении ξ, стремящемся к нулю, длительность импульса сокращается.

Функция v(t) при ξ стремящемся к нулю, называется дельта-функцией, или функцией Дирака (см. рис. 1.8, б): σ(t - t₀) = {0  при t ≠ t₀;  ∞  при t = t₀}

∞    ∫ σ(t)dt = 1   -∞

Дельта-функция, будучи равной нулю, кроме точки t = t₀, обладает единичным

интегралом 

Поэтому она является математической моделью бесконечно короткого внешнего воздействия с единичной площадью.

Функция включения и дельта-функция связаны между собой соотношениями:

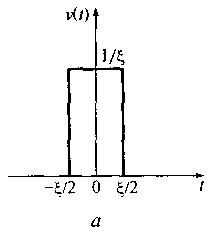
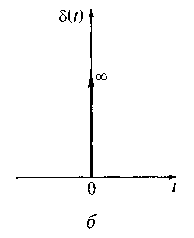
Рис. 1.8. Прямоугольный импульс (а) и символьное изображение дельта-функции (б)

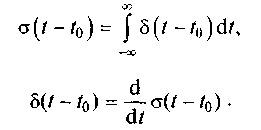(1.4)(1.5)

Следовательно, функция включения представляет собой ин­теграл от дельта-функции, а дельта-функция — производную от функции включения.

Фильтрующее свойство дельта-функции

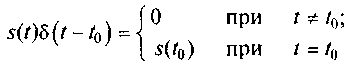(1.6)

позволяет отследить значение произвольного сигнала s(t) в фик­сированный момент времени t = t₀. Во всех остальных точках вре­менной оси значение произведения дельта-функции на произволь­ную функцию s(t) равно нулю. Учитывая это, с помощью дельта-функции можно выделять значение сигнала в произвольный мо­мент времени t₀.