Сигналы и их детерминированные модели. Спектральное представление детерминированных сигналов (1, 2 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 7

Динамическое представление сигнала функцией включения. До­пустим, что имеется непрерывный произвольный сигнал s(t). На рис. 1.9 показано динамическое представление сигнала функцией включения. Выделим на положительной оси времени дискретные моменты t_k= kΔt при k ≥ 1 , кратные постоянному шагу дискретиза­ции Δt. В момент времени t_k сигнал s(t) принимает значение s_k = s(t_k). Пусть s₀ = s(t) при t = 0. Тогда текущее значение сигнала при t_k-1 < t ≤ t_k приближенно равно сумме функций включения, амп­литуды которых равны разности значений s_k и s_k-1 функции s(t) в моменты времени t_k и t_k-1

Следовательно,

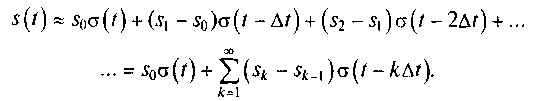
Если временной интервал  Δt устремить к нулю, то дискретную переменную kΔt можно заменить непрерывной переменной τ. Ма­лые приращения Δs_k = s_k - s_k-1 функцией включения превра­щаются в дифференциалы ds = (ds/dτ)dτ.

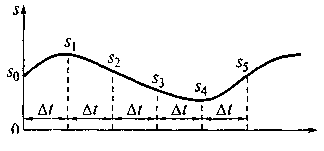
Рис. 1.9. Динамическое представление сигнала функцией

В результате подобных преобразований получим формулу динамического представления произвольного сигнала посредством функций включения:

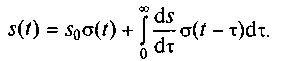 (1.7)

Динамическое представление сигнала дельта-функцией. Исход­ный сигнал s(t) в моменты времени t_k-1 ≤ t≤ t_k может быть пред­ставлен в виде суммы элементарных импульсов η_k(t) = s_k[σ(t - t_k) - σ(t - t_k- Δt)] с амплитудой s_k = s(t_k):

	∞ s(t) = Σ ηk(t)         k= -∞

 

                                                                                        (1.8)

В сумме (1.8), описывающей сигнал s(t) в момент времени t_k-1 ≤ t≤ t_k , отличным от нуля будет только один член, соответ­ствующий k-му отсчету.

Подставляя в (1.8) значение элементарного импульса, произ­водя деление и умножение выражения для s(t) на величину шага взятия отсчетов Δt, получим

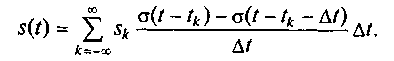(1.9)

В выражении (1.9), переходя к пределу при шаге Δt, стремя­щемся к нулю, можно заменить суммирование интегрированием по переменной τ. Дифференциал этой переменной dτ будет отве­чать величине Δt при условии, что

В результате подобных преобразований получим формулу ди­намического представления сигнала с использованием дельта-функции:

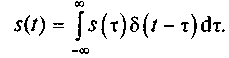(1.10)

1.4. Ортогональные сигналы и обобщенные ряды Фурье

Энергия сигнала s(t), выделяемая на сопротивлении, равному 1 Ом, определяется интегралом от квадрата сигнала s²(t) по всей оси времени:

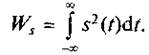(1.11)

Таким образом, используя выражение (1.11), можно провести сравнение сигналов относительно энергии, развиваемой ими в сопротивлении, равном 1 Ом.

Пусть на вход устройства воздействуют два сигнала s₁(t) и s₂(t) с энергиями соответственно  W_s1 и W_s2

Энергия суммы двух сигналов будет иметь вид

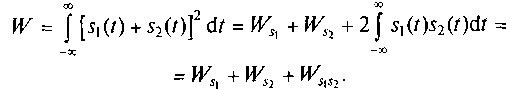(1.12)

Из выражения (1.12) видно, что энергия суммы двух сигналов в общем виде не равна сумме энергий этих сигналов. Энергия сум­марного сигнала заключает в себе так называемую взаимную энергию сигналов.

Сигналы s₁(t) и s₂(t) называются ортогональными, если их вза­имная энергия равна нулю, т.е.

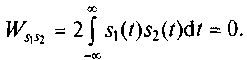(1.13)

Пусть на временном интервале [t₁, t₂] задано множество сигна­лов {s₀, s₁, s₂, ...}, попарно ортогональных друг другу и обладаю­щих нулевой взаимной энергией. Тогда

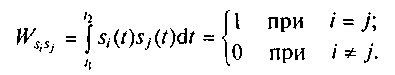(1.14)

Условие (1.14) говорит о том, что в пространстве сигналов определен ортонормированный базис, образованный функциями s_i. Используя этот базис, произвольный сигнал s(t) может быть пред­ставлен рядом

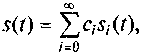(1.15)

который называется обобщенным рядом Фурье сигнала s(t) в выб­ранном базисе ортонормированных функций s_i.

Постоянный коэффициент обобщенного ряда Фурье

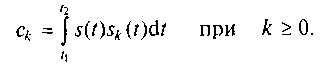(1.16)

Используя (1.15) с определенными по формуле (1.16) коэф­фициентами c_k и множество ортонормированных функций из выб­ранного базиса, можно провести аппроксимацию любого сложного сигнала. Под аппроксимацией в данном случае понимают разложение сложного сигнала на более простые функции (сигна­лы) из базиса ортонормированных функций, каждая из которых имеет амплитуду, определенную формулой (1.16).

Представление сигналов в виде обобщенных рядов Фурье име­ет важное практическое значение, так как вместо того, чтобы изучать функциональную зависимость сложного сигнала в беско­нечном множестве точек, исследователь может характеризовать сигнал системой коэффициентов обобщенного ряда Фурье (1.16).

1.5. Ортонормированные базисы в радиотехнике

Из множества возможных ортонормированных базисов рассмот­рим базисы, наиболее применимые в радиотехнике.

Ортонормированная система гармонических функций. Пусть пе­риод изменения сложного сигнала равен Т. Для описания сигнала u(t) используется временной интервал [0,Т], постоянное число u₀ = 1 /√T и множество тригонометрических функций с частотами 2πт/ Т, кратными частоте изменения исходного сигнала ω₁ = 2π /Т. Эти функции и образуют ортонормированный базис. На рис. 1.10 показан вид первой, второй, третьей и четвертой базисных функ­ций тригонометрического ряда Фурье.

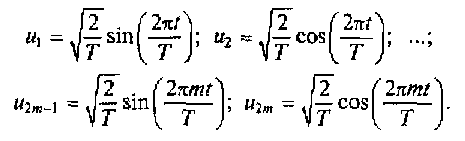(1.17)

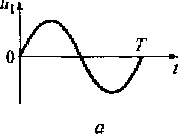
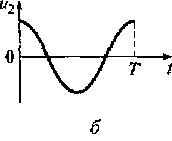
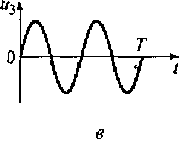
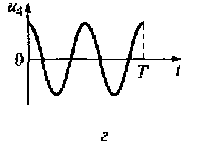
Рис. 1.10. Вид первой (а), второй (б), третьей (в) и четвертой (г) базис­ных функций тригонометрического ряда Фурье

Для проверки ортогональности функций (1.17) вычислим взаимную энергию для нескольких пар этих функций, например:

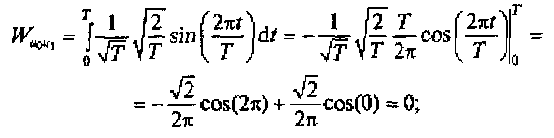
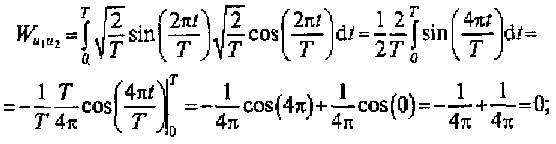
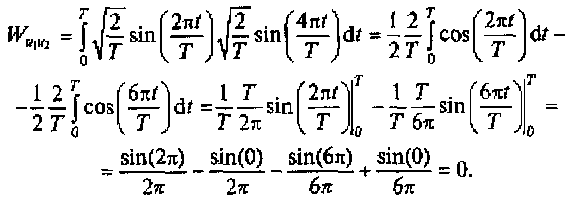
Дальнейшие вычисления также будут приводить к равенству нулю взаимных энергий пар функций (1.17), что говорит об орто­гональности гармонических функций.

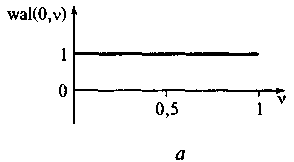
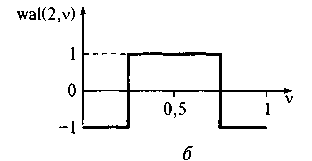
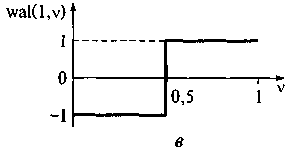
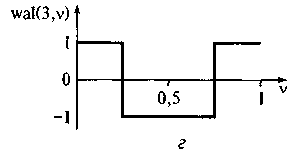
Ортонормированная система функций Уолша. Обработка диск­ретных сигналов ориентирована на использование ортонормированной системы функций Уолша, которые на отрезке своего су­ществования [0,Т] принимают лишь значения ±1. Для рассмотре­ния этих функций введем безразмерное время v = t/T. Обозначим k-ю функцию Уолша символом wal(k,v). Описание функций Уол­ша аналитическими выражениями сложно, однако построение си­стемы функций Уолша можно проследить. На рис. 1.11 приведены графики нулевой, первой, второй и третьей функций Уолша.