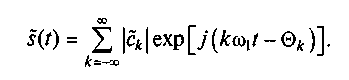(2.14)
В выражении модули коэффициентов |ck| , соответствующие отрицательным |c-k| и положительным |ck| индексам, равны между собой. Аргументы θ-k и θk симметричны относительно начала координат (kw1t = 0 при k = 0). Это позволяет представить комплексный ряд Фурье (2.14) в более удобной форме:
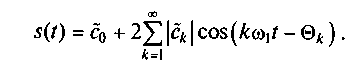
Учитывая (2.13), тригонометрический ряд Фурье окончательно принимает следующий вид:
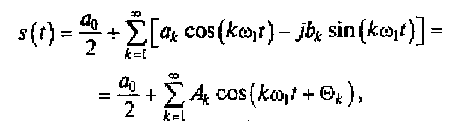(2.15)
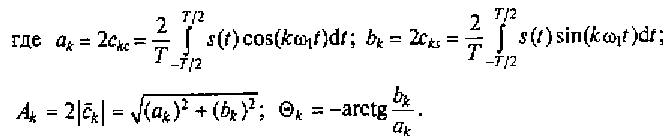
Рассматривая тригонометрический ряд Фурье (2.15) и коэффициенты, входящие в него, можно обнаружить следующие свойства:
если сигнал описывается четной функцией (сигнал симметричен относительно начала координат s(-t) = s(t) и достигает максимума при t = 0), то в ряде Фурье коэффициенты bk будут равны нулю;
если сигнал описывается нечетной функцией (при t = 0 сигнал достигает минимального значения), то в ряде Фурье коэффициенты ak будут равны нулю;
структура частотного спектра исходного сигнала полностью определяется спектром амплитуд (модули коэффициентов At) и спектром фаз (аргументы θk комплексных коэффициентов);
спектр амплитуд периодического сигнала является дискретным.
Он состоит из отдельных спектральных составляющих, каждая из которых имеет свою частоту 0, ω1, ω2 = 2ω1, ω3 = 3ω1 ... и свою амплитуду. На рис. 2.4 представлен спектр амплитуд для коэффициентов |ck| , а на рис. 2.5 — для коэффициентов Ak = 2|ck|, соответствующих одному и тому же сигналу;
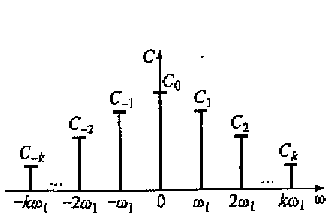
Рис. 2.4. Спектр амплитуд для коэффициентов |ck| комплексного ряда Фурье
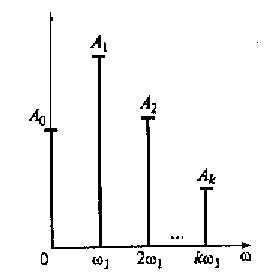
Рис. 2.5. Спектр амплитуд для коэффициентов Ak тригонометрического ряда Фурье
ширина спектра периодического сигнала определяется частотой спектральной составляющей (ωq = qω1), имеющей амплитуду на оговоренном (заданном) уровне, например, амплитуда составляет 0,707 максимальной амплитуды какой-либо спектральной составляющей.
Возможность разложения сложных периодических сигналов на спектральные составляющие является мощным инструментом при проведении анализа прохождения сигналов через линейные цепи. Для этого можно, например, использовать метод спектрального анализа. Особенность его состоит в следующем.
Пусть имеется линейная электрическая цепь, на вход которой воздействует сложный периодический сигнал. Необходимо найти напряжение на выходе цепи.
1 . Периодический сигнал описываем рядом Фурье:
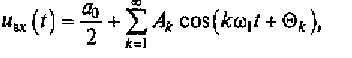
для которого вычисляем амплитуды Ak и фазы θk спектральных составляющих.
2. Определяем комплексный коэффициент передачи линейной цепи K(jω) = K(ω)ехр(jφ), где K(ω)— модуль, а φ(ω) — аргумент коэффициента передачи цепи.
3. Учитывая связь функции cos(x) с экспоненциальной функцией cos(x) = [ехр(jx) + ехр(-jх)]/2, поскольку ехр(±jх) = cos(x) ± jsin(x), запишем мгновенный комплекс для k-й спектральной составляющей входного сигнала, описываемого рядом Фурье:
uвхk (t) = Ak (kω1) exp {j [kω1t + θk (kω1)]} ,
где Ak (kω1) и θk (kω1) - модуль (амплитуда) и аргумент (фаза) k-й спектральной составляющей на частоте kω1.
4. Определяем мгновенный комплекс отклика сигнала на выходе линейной цепи относительно каждой спектральной составляющей входного сигнала, описанного рядом Фурье:
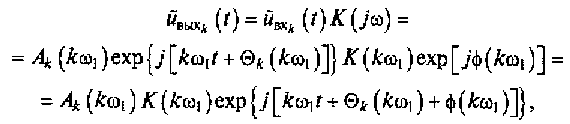
где K(kω1) и φ (kω1) — модуль и аргумент комплексного коэффициента передачи линейной цепи на частоте ω = kω1.
5. Записываем мгновенный комплекс полного отклика линей ной цепи:
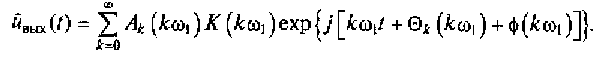
6. Переходя от экспоненциальной функции ехр(х) к функции cos(x), определяем мгновенное значение сигнала на выходе линейной цепи:
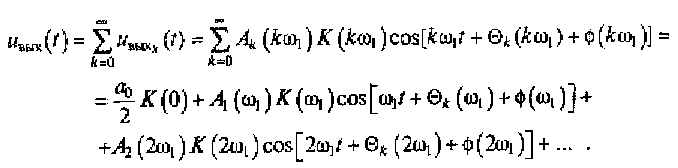
Метод спектрального анализа достаточно нагляден при изучении прохождения периодических сигналов через линейную цепь, однако он имеет существенный недостаток. Действительно, исходные сигналы могут иметь сложную форму. При этом число членов ряда Фурье будет большим при стремлении получить приемлемую точность анализа, что приводит к объемным математическим вычислениям.
Пример 2.4. Используя описание периодического сигнала из примера 2.3, необходимо аппроксимировать его тригонометрическим рядом Фурье.
Решение. Исходный сигнал является нечетной функцией, поэтому для его аппроксимации вычисляем коэффициенты а0/2, bk и аргументы θk ряда (2.15):
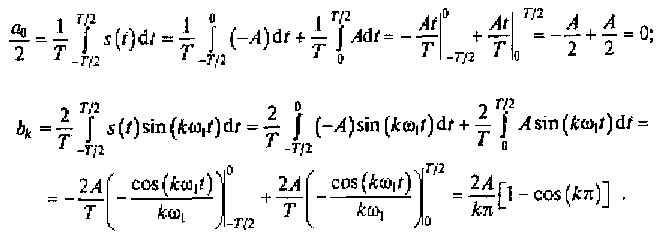
Окончательно коэффициенты bk можно представить в виде
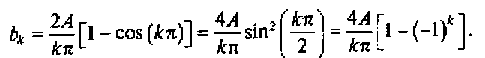
Сигнал в примере является нечетной функцией, поэтому все коэффициенты ak будут равны нулю. Тогда
Θk = -arctg (bk/ak) = -arctg (bk/0) = -arctg (∞) = -π/2.
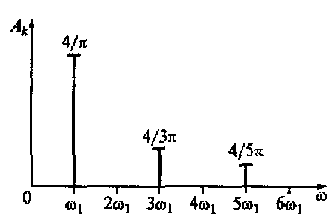
Рис. 2.6. Амплитудный спектр периодического сигнала
Учитывая значения коэффициентов a0/2, bk и аргументов Θk, ряд Фурье, описывающий периодический сигнал, будет иметь вид
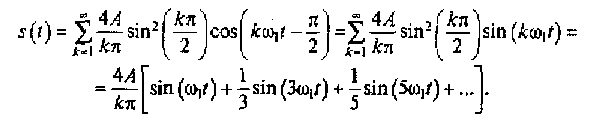
Эта формула по виду совпадает с выражением, полученным в примере 2.3, что говорит о вычислении спектров периодических сигналов с использованием тригонометрических рядов Фурье, представленных в форме (2.10) или (2.15).
На рис. 2.6 показан амплитудный спектр Ak периодического сигнала (см. рис. 2.3), полученный в соответствии с выражением (2.15), а на
рис. 2.7 — спектр |ck| = Ak /2 комплексного ряда Фурье (2.14) для периодического сигнала.
В соответствии с рядом, полученным в примере 2.4, на рис. 2.8 показано суммирование различных спектральных составляющих ряда Фурье. На рисунке видно, что аппроксимация сложных сигналов рядом Фурье позволяет разложить эти сигналы на множество более простых сигналов. При этом сумма множества простых аппроксимирующих сигналов дает описание исходного периодического сигнала.
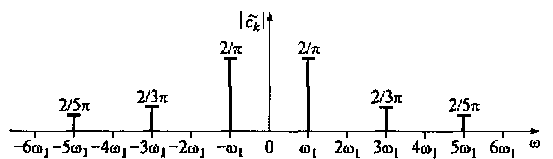
Рис. 2.7. Спектр комплексного ряда Фурье для периодического сигнала
Пример 2.5. На рис. 2.9 показана электрическая линейная цепь. Используя последовательность прямоугольных импульсов из примера 2.4 в качестве входного сигнала линейной цепи (зажимы 1 — 1), необходимо найти сигнал на выходе (зажимы 2—2) этой цепи.
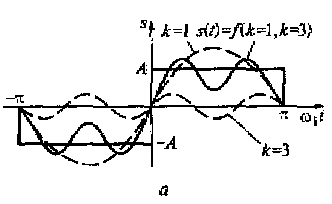
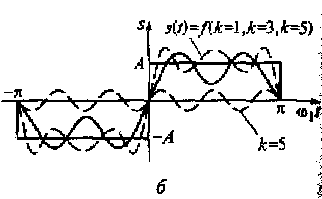
Рис. 2.8. Суммирование 1-й и 3-й гармоник (а), 1-й, 3-й и 5-й гармоник (б) ряда Фурье
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.