Сигналы и их детерминированные модели. Спектральное представление детерминированных сигналов (1, 2 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 8

Рис. 1.11. Графики нулевой (а), первой (б), второй (в) и третьей (г) функций Уолша

Разложение сложного сигнала, заданного на отрезке времени [0,Т] или [-Т/2, Т/2], в обобщенный ряд Фурье по функциям Уолша представляется в виде

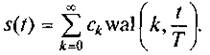(1.18)

ГЛАВА  2

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ДЕТЕРМИНИРОВАННЫХ

СИГНАЛОВ

2.1. Аппроксимация произвольных сигналов

Сигналы делят на периодические и непериодические. Периоди­ческий сигнал представляет собой детерминированный сигнал, мгновенные значения которого повторяются через равные проме­жутки времени. Параметр Т, равный наименьшему интервалу вре­мени, через который повторяются мгновенные значения перио­дического сигнала, называется периодом. Таким образом, перио­дические сигналы удовлетворяют условию

(2.1)

где n — любое целое число.

Непериодические сигналы условию (2.1) не удовлетворяют.

К основным энергетическим характеристикам сигналов относят их энергию и мощность. Под электрической энергией W понимают работу за определенный интервал [t₁, t₂], затрачиваемую на перемещение положительного заряда   q между двумя точками электри­ческой цепи, разность потенциалов между которыми равна и. Согласно определению

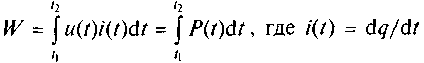
- ток протекающий в цепи; P(t) – мгновенная мощность сигнала.

Мгновенная мощность P(t) произвольного сигнала s(t), описы­ваемого мгновенными значениями напряжения u(t) и тока i(t), рассчитывается по формуле P(t) = u(t)i(t).

Если сопротивление участка цепи равно 1 Ом, то средняя мощ­ность принимает вид P(t) = u²(t) = i²(t). В этом случае энергия в пределах рассматриваемого интервала времени [t₁, t₂] описывает­ся выражением

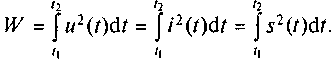(2.2)

Тогда средняя мощность на интервале [t₁, t₂]

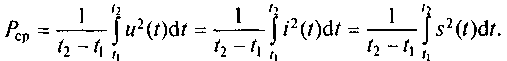(2.3)

При анализе прохождения сигналов через радиотехнические цепи важным является представление (аппроксимация) реальных детер­минированных сигналов. В качестве критерия качества аппроксима­ции используют разность мощностей или энергий реального сигнала и предлагаемой модели сигнала, которая должна быть минималь­ной.

Допустим, что произвольный сигнал s(t) аппроксимируется функцией η(t) в интервале времени [t₁, t₂]. Тогда можно записать

где с — постоянный коэффициент, характеризующий степень не­совпадения сигнала s(t) и аппроксимирующей функции η(t).

Отличие сигналов s(t) и cη(t) можно описать функцией ошиб­ки ξ(t) = s(t) - cη(t). В этом случае в качестве критерия оценки точности аппроксимации исходного сигнала можно использовать среднее значение квадрата функции ошибки (средняя мощность сигнала ошибки):

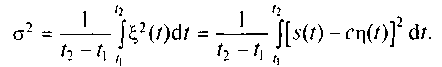
Сигналы совпадают, если значение коэффициента с определя­ется выражением

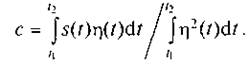(2.4)

Таким образом, аппроксимирующий коэффициент с опреде­ляется отношением взаимной энергии произвольного сигнала s(t) и аппроксимирующего сигнала η(t) к энергии аппроксимирую­щего сигнала η(t).

В общем случае коэффициент с не равен нулю. Однако когда сигналы полностью не

 подобны, то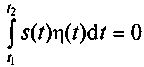а значит, и коэффициент с также будет равен нулю. Равенство нулю коэффи­циента с говорит об ортогональности сигналов s(t) и η(t) в ин­тервале [t₁, t₂].

Пример 2.1. Имеется периодическая последовательность разнополярных прямоугольных импульсов амплитудой ±А (рис. 2.1). Период повторе­ния сигнала равен Т. Необходимо аппроксимировать этот сигнал функ­цией η(t) = sin(ωt).

Решение. Исходный сигнал повторяется с периодом Т, поэтому для его аппроксимации можно использовать интервал времени [0, Т].

С целью аппроксимировать исходный сигнал функцией η(t) опреде­лим значение коэффициента с по формуле (2.4):

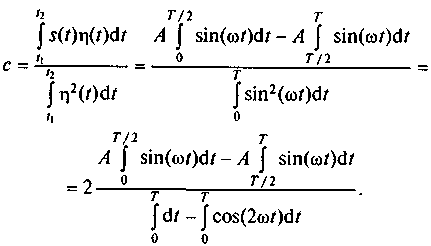
С учетом того, что для периодических сигналов выполняется условие ωТ= 2π, полученное выражение можно свести к виду

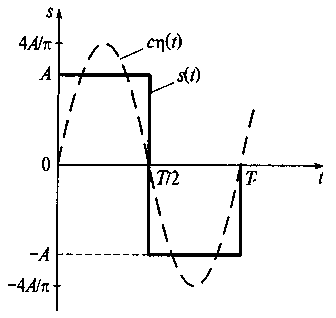
Рис. 2.1. Вид разнополярного прямо­угольного импульса

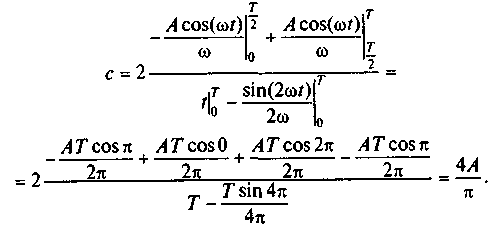
Степень совпадения исходного сигнала s(t) и аппроксимирующей фун­кции η(t) определяется коэффициентом с = 4А/π, который является амплитудой функции sin(ωt). С учетом выражения (2.3) сигнал s(t) можно описать формулой

В большинстве случаев аппроксимировать сложный сигнал од­ной функцией с достаточной степенью точности невозможно, что видно из рис. 2.1. Однако при аппроксимации сигналов можно использовать множество аппроксимирующих функций η₀(t), η₁(t) , η₂(t), ..., η_k(t), где k — номер аппроксимирующей функции. В этом случае каждая из этих функций будет вносить свой вклад в точ­ность аппроксимации исходного сигнала, т. е.

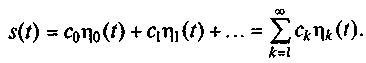
Таким образом, выбрав аппроксимирующие функции η_k(t) и определив коэффициенты аппроксимации c_k, исходный сигнал s(t) можно представить суммой произведений функций η_k(t) и коэффициентов c_k. Рассмотрим на примерах возможности аппрок­симации сложных сигналов.

2.2. Описание сложных периодических сигналов рядом Фурье

Точность аппроксимации исходного сигнала s(t) множеством аппроксимирующих функций η₀(t), η₁(t) , η₂(t), ... характеризует­ся равенством нулю разности энергий исходного сигнала и аппроксимирующих функций

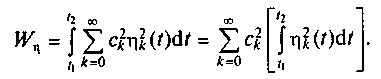
Значения коэффициентов c_k, k ≥  0 могут быть рассчитаны по формуле

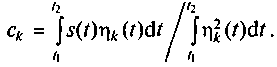(2.5)

Доказано, что если коэффициенты аппроксимирующей функ­ции определяются в соответствии с выражением (2.5), то сложный периодический сигнал может быть описан обобщенным ря­дом Фурье:

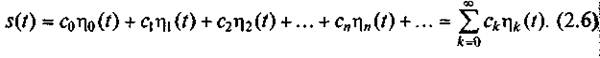
Для упрощения вычислений в качестве множества аппроксимирующих функций { η_k, k≥0} используют ортонормированные функции, которые попарно отвечают условию ортогональности:

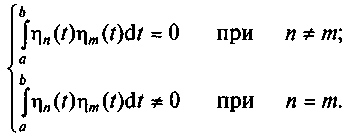(2.7)

Из (2.7) следует, что для базиса ортогональных функций взаимная энергия двух функций не равна нулю только при равенстве между собой индексов этих функций. Таким образом, нулю не равна энергия от функции, которая умножена сама на себя, если при этом она сама не равна нулю.

Если для функции η_n(t) выполняется условие

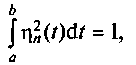(2.8)

то подобная функция называется нормированной. Функции, отве­чающие условиям (2.7) и (2.8), называются ортонормированными. Базис (множество) подобных функций и используется в качестве системы действительных функций при описании сложного пери­одического сигнала обобщенным рядом Фурье (2.6).