Как правило, шаг дискретизации Δt = tj + 1 - tj выбирают постоянным (см. рис. 1.2). Преимущество дискретных сигналов перед аналоговыми заключается в отсутствии необходимости отслеживать форму сигнала во все моменты времени, а необходим лишь факт наличия или отсутствия импульса.
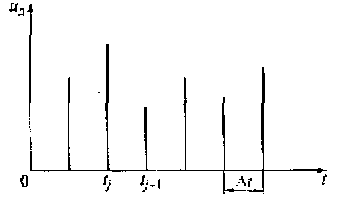
Рис. 1.2. Модель дискретного сигнала
Разновидностью импульсных сигналов являются цифровые сигналы, под которыми понимают сигнал, в котором амплитуды от импульса к импульсу остаются постоянными, а момент появления импульса и его длительность являются случайными величинами.
Случайные сигналы представляют собой различные флуктуационные процессы, значения которых в конкретные моменты времени можно предсказать с вероятностью, отличной от единицы. Как правило, эти сигналы проявляют себя как помехи и препятствуют извлечению информации из принятого колебания.
В качестве второго классификационного признака сигналов можно использовать размерность пространства, в котором существует сигнал. Например, ток или напряжение в большинстве радиотехнических устройств можно рассматривать как одномерный сигнал, зависящим от времени. Распределение токов и напряжений в длинной линии представляет собой сигнал, зависящий от двух переменных: времени и пространства. Звуковое давление в зависимости от пелен, которые преследуются, можно рассматривать как одно-, двух-, трех- и четырехмерный сигнал, зависящий от времени и одной, двух или и трех пространственных координат.
Отмеченные ранее классификационные признаки сигналов, как физических процессов можно изучать с помощью различных приборов и устройств (осциллограф, вольтметр, приемник), Однако наблюдаемые с помощью приборов явления всегда выступают как частные проявления, что не позволяет говорить об их свойствах, предсказать поведение сигналов в пространстве и времени. Для устранения этого недостатка необходимо описать сигнал, т.е. создать его математическую модель. Математическое описание сигналов позволяет абстрагироваться от конкретной природы носителя сигнала. используя одну и ту же математическую модель сигнала для описания различных явлений (тока, напряжения, напряженности электромагнитного поля и т.д.).
Существуют различные способы описания сигналов, например в виде аналитических выражений или таблиц для аналоговых сигналов, в виде вероятностных функций для случайных процессов. В соответствии с этим сигналы можно классифицировать относительно математической формы их представления. В этом случае сигналы могут быть разделены на детерминированные и стохастические.
Детерминированными сигналами называются сигналы, значения которых в любые моменты времени являются известными величинами или могут быть заранее вычислены. Слово «детерминизм» происходит от латинского determitiarlo, означающего определение либо учение об объективной закономерной взаимосвязи и причинной обусловленности всех явлений. Анализ детерминированных сигналов опирается на классическую теорию дифференциальных уравнений. Математическая модель детерминированных сигналов позволяет предсказывать их мгновенные значения в любые моменты времени с вероятностью равной единице. Детерминированные сигналы могут быть описаны математическими формулами, вычислительными алгоритмами, таблицами и т, д.
Случайные (стохастические) сигналы представляют сигналы, мгновенные значения которых являются случайными величинами. Анализ этих сигналов основан на теории вероятностей и теории случайных процессов. Значения случайных сигналов можно предсказать только с вероятностью меньше единицы для любой базовой переменной.
Строго говоря, в природу детерминированных сигналов не существует. Это объясняется тем, что радиотехнические системы
взаимодействуют с окружающими их физическими объектами, которые оказывают влияние па эти системы, В радиокомпонентах присутствуют хаотические тепловые флуктуации. Как правило, имеет место неполная информация о начальном состоянии системы. Bee это заставляет рассматривать реальные сигналы как случайные функции времени.
При выборе модели сигнала исследователь получает возможность описания тех свойств сигналов, которые наиболее важны для него. Это позволяет не рассматривать большое число второстепенных признаков. В то же время, опираясь на математические модели сигналов, можно сравнивать процессы, проводить классификацию, предсказывать их поведение в тех или иных условиях.
1.2. Описание детерминированных сигналов разрывными
функциями
При анализировании прохождения сигналов через радиотехнические цепи возникает задача представления сигнала в виде математического выражения. Предположим, что аналоговый сигнал s(t) может быть описан с использованием тригонометрических s(t) = Asin(t) или s(t)= Аcos(t), экспоненциальных s(t) = Aexp(t) и логарифмических s(t) = Aln(t) функций, где А — коэффициент пропорциональности, t — аргумент функции.
На рис. 1.3 показаны прямоугольный и трапецеидальный импульсы. Импульсные сигналы могут быть описаны с использованием разрывных функций. Например, прямоугольный импульс (см. рис.1.3, а) описывается функцией
U(t) = {0 при t < 0 ; Uп при 0 ≤ t ≤ τи ; 0 при t > τи}
где Uп — амплитуда импульса; τи — длительность импульса.
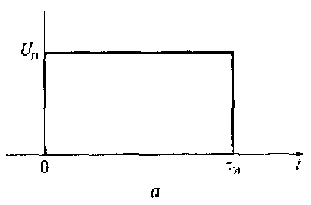
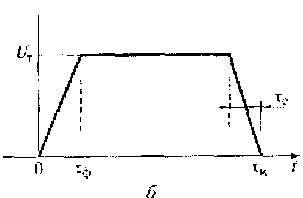
Рис. 1.3. Прямоугольный (а) и трапецеидальный (б) импульсы
Для трапецеидального импульса (см. рис. 1.3, б) справедливо аналитическое определение:
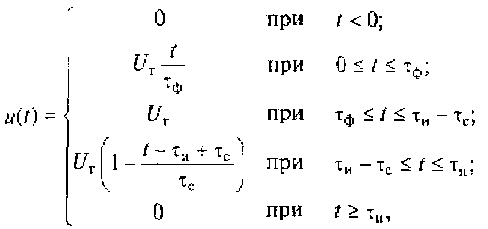
где Uт — амплитуда импульса; τφ — длительность переднего фронта импульса; τс — длительность среза (заднего фронта) импульса; τи — длительность импульса.
Таким образом, разбивая сигнал на отдельные части, описываемые простейшими функциями (уравнением прямой, тригонометрическими или экспоненциальными функциями и т.д.) в разные моменты времени, можно получить формулу для описания сложного сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.