Сигналы и их детерминированные модели. Спектральное представление детерминированных сигналов (1, 2 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 12

При использовании в качестве ортонормированного базиса гар­монических функций средняя мощность сложного сигнала может быть представлена в виде

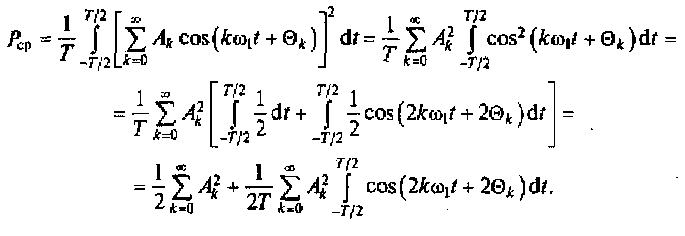
Интеграл во втором слагаемом равен нулю, так как интеграл от гармонической функции за период ее изменения равен нулю. Тогда формулу можно преобразовать к виду

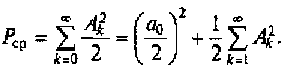
Таким образом, средняя мощность периодического сигнала мо­жет быть описана суммой квадратов амплитуд спектральных со­ставляющих, на которые разлагается сложный сигнал.

2.6. Спектральный анализ непериодических сигналов

Известно, что сигналы могут быть как периодическими, так и непериодическими. Выражения (2.15) и (2.16) позволяют аппрок­симировать сложный периодический сигнал рядом Фурье, Учиты­вая, что множество сигналов в радиотехнических устройствах яв­ляются непериодическими функциями, распространим выраже­ния, относящиеся к ряду Фурье, на непериодические сигналы.

Допустим, что имеется непериодический сигнал s(t) в виде одиночного импульса, показанного на рис. 2.12, отличный от нуля на временном интервале [t₁, t₂] Определим для этого импульса интервал времени [0, Т], на котором он существует.

Представим сигнал в виде последовательности импульсов с периодом повторения Т, как это показано на рис. 2.13. Для периодической функции разложе­ние сигнала в ряд Фурье приво­дит к получению дискретного спектра. При этом согласно (2.15) каждому коэффициенту a_k соот­ветствует круговая частота kω₁ = k2π/T, где  ω₁ = 2π/Т — круговая частота повторения периоди­ческого сигнала. Например, при k= 1  ω₁ = 1 · 10⁶ рад/с, при k = 2  kω₁ = 2 · 10⁶ рад/с, при k = 3 kω₁ = 3 · 10⁶ рад/с и т.д. Таким обра­зом, составляющие спектра сигнала отстоят друг от друга на ве­личину ω₁.

Рис. 2.12. Одиночный импульс

Если для периодического сигнала период T устремить к беско­нечности, то возвращаемся к одиночному импульсу, т.е. непери­одическому сигналу (см. рис. 2.12), и поэтому ω₁ = 2π/Т будет стре­миться к бесконечно малой величине dω, а частоты спектральных составляющих  kω₁  будут представлять собой текущие частоты ω.

В этом случае интеграл 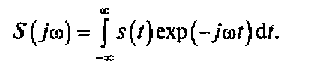 является функ­цией круговой частоты ω и называется спектральной плотностью сигнала s(t). Когда интервал интегрирования неопределен, спект­ральная плотность сигнала рассматривается в диапазоне частот от - ∞ до + ∞, т.е.

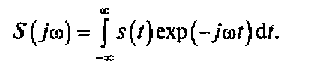(2.17)

При этом

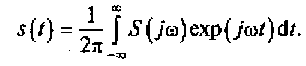(2.18)

Выражение (2.17) называется прямым, а (2.18) — обратным преобразованиями Фурье. Первое из этих выражений позволяет про­вести анализ непериодических сигналов в частотной области, а второе — во временной области, т.е. восстановить сигнал по его спектральной плотности.

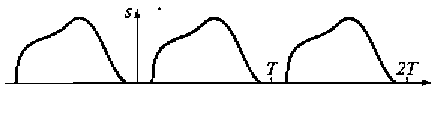
Рис. 2.13. Приведение одиночного импульса к периодическому сигналу

Из выражения (2.17) видно, что спектральная плотность сиг­нала является комплексной величиной. Однако характеристики реальных физических процессов представляют собой действитель­ные величины. Рассмотрим это относительно спектральной плот­ности, для чего экспоненциальную функцию в выражении (2.17) представим в виде суммы функций cosx и sinx:

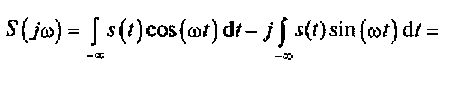
= A(ω) – jB(ω) = S(ω)exp[jψ(ω)]                          (2.19)

где A(ω) = ∫ s(t)cos(ωt)dt и B(ω) = ∫ s(t)sin(ωt)dt - действительная и мнимая части спектральной плотности; S (ω) = √A²(ω) + B²(ω) и

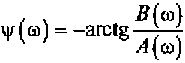  - модуль и аргумент спектральной плотности непериодического сигнала.

Пример 2.6. Имеется одиночный прямоугольный импульс (рис. 2.14) длительностью τ_и и амплитудой А. Необходимо вычислить спектральную плотность импульса.

Решение. Воспользовавшись формулой (2.17), получим

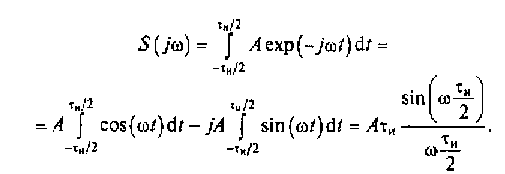(2.20)

Из полученного выражения видно, что модуль спектральной плотно­сти сигнала определяется действительной частью спектральной плотности:

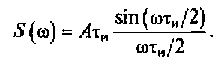(2.21)

При ω = 0 модуль спектральной плотности S(ω) достигает макси­мального значения. В выражении (2.21) при ωτ_и /2 = kπ  функция синус равна нулю, что выполняется на частотах ω = 2kπ /τ_и. В этом случае модуль спектральной плотности S(ω) прямоугольного импульса также будет ра­вен нулю (рис. 2.15).

Аргумент (2.19) спектральной плотности прямоугольного импульса можно рассчитать по формуле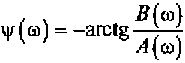. Так как мнимая часть спектральной плотности  B(ω) = 0, то аргумент в различных диапазо­нах частот принимает следующие значения.      В диапазоне -2π/ τ_и ≤ ω ≤ 2π/ τ_и

Рис. 2.14.  Одиночный прямоугольный импульс

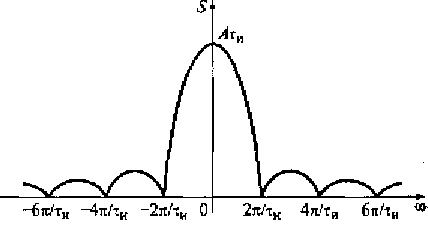
Рис. 2.15. Модуль спектральной плотности прямоугольного импульса

аргумент равен нулю. В диапазонах -4π/τ_и ≤ ω ≤ -2π/τ_и и 2π/τ_и ≤ ω ≤ 4π/τ_иаргумент составляет соответственно π и -π. В диапазонах -6π/τ_и ≤ ω ≤ -4π/τ_и и 4π/τ_и ≤ ω ≤ -6π/τ_иаргумент равен соответственно 2π и -2π и т.д. Это наглядно видно из рис. 2.16, на котором показана фазочастотная характеристика спектральной плотности прямоугольного импульса.

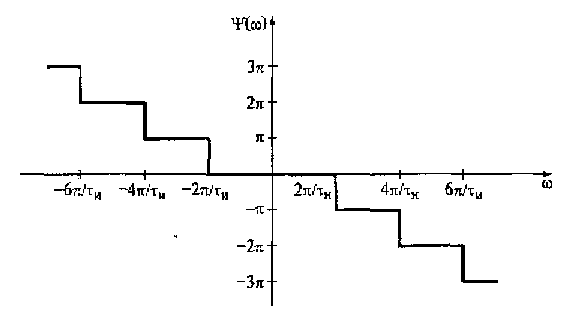
Рис. 2.16. Фазочастотная характеристика спектральной плотности прямоугольного импульса

Рассматривая выражение (2.20) относительно спектральной плотности прямоугольного импульса, можно отметить следующее. При увеличении длительности импульса модуль спектральной плотности при ω = 0 увеличивается, однако значение частоты, которой модуль спектральной плотности обращается в нуль, с ростом длительности импульса уменьшается. Это говорит о том, что ширина спектра прямоугольного импульса сужается при увеличении длительности импульса.

Пример 2.7. Имеется треугольный импульс (рис. 2.17),

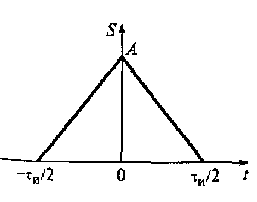
Рис. 2.17. Треугольный им­пульс

форма которого описывается выражением

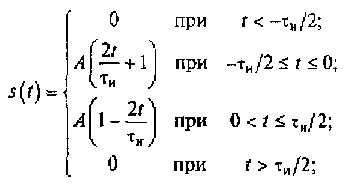
Необходимо определить спектральную плотность этого сигнала.

Решение. Подставив в (2.17) аналитическое описание треугольного импульса, получим

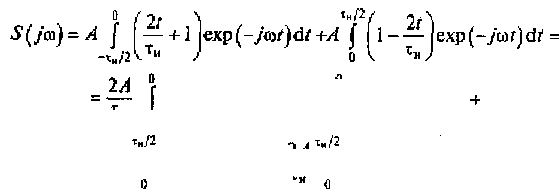
Осуществив интегрирование, находим

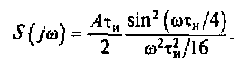(2.22)

В выражении (2.2) множитель Аτ_и/2 определяет площадь треугольно­го импульса (см. рис. 2.17). Второй множитель в этом выражении равен нулю тогда, когда функция sin(ωτ_и/2) = 0, что происходит при выполне­нии условий ωτ_и/4 = ±π, ±2π, ..., ±kπ, ± ... . Отсюда можно найти частоты, на которых модуль спектральной плотности равен нулю: ω = ±4π/τ_и, ±8π/τ_и, ...,±4kπ/τ_и, где k = 1,2, ... . Это наглядно видно из рис. 2.18, на котором изображена спектральная плотность сигнала, представляющего собой тре­угольный импульс.