Решение. Используем метод спектрального анализа. Сигнал на входе линейной цепи может быть представлен рядом Фурье (см. разложение сигнала в примере 2.4):
uвх (t) = Σ 4A/kπ sin2(kπ/2) cos(kω1t – π/2).
Комплексный коэффициент передачи линейной цепи от зажимов 1-1 к зажимам 2 - 2 описывается функцией с постоянной времени τ = RC:
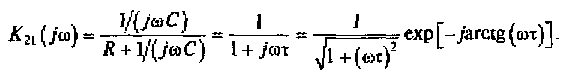
Мгновенный комплекс входного сигнала относительно k-й спектральной составляющей
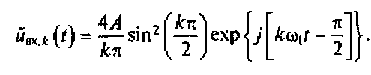
Используя значение мгновенного комплекса для k-й спектральной составляющей сигнала входного воздействия и комплексный коэффициент передачи линейной цепи, записываем выражение, описывающее мгновенный комплекс для k-й спектральной составляющей выходного сигнала:
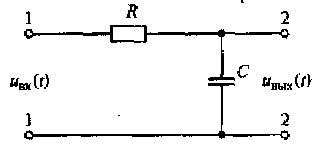
Рис. 2.9. Линейная электрически цепь
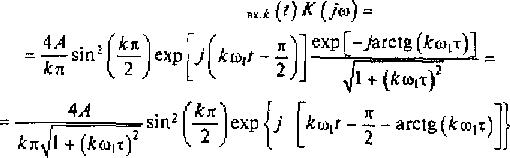
Суммируя мгновенные комплексы спектральных составляющих выходного сигнала, определим мгновенный комплекс отклика линейной цепи
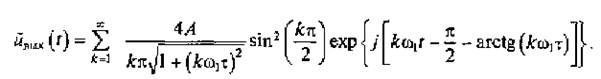
Перейдем от мгновенного комплекса выходного сигнала к мгновенному значению этого сигнала:
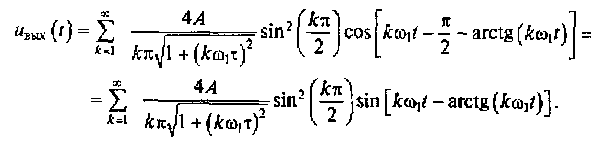
Рассчитаем амплитуды нескольких спектральных составляющих выходного сигнала. Для этого примем, что А = 1 В, R = 1 кОм, С = 1000 пФ, f1 = 16 кГц. Тогда ω1 = 2πf1 = 105 рад/с и ω1τ = ω1RC = 0,1.
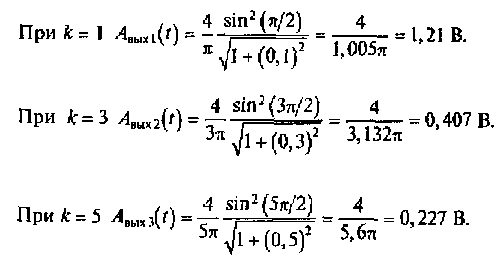
Из примера 2.5 видно, что при прохождении сигнала сложной формы через линейную цепь амплитуды его спектральных составляющих уменьшаются, т.е. происходит искажение выходного сигнала. Так, амплитуда первой гармоники уменьшилась на 0,5%, третьей гармоники — на 4%, а пятой гармоники — на 12 %. Амплитуда каждой последующей гармоники выходного сигнала будет снижаться пропорционально √1+(kω1RС)2 . Кроме того, фаза каждой гармоники выходного сигнала изменяется
на величину -arctg(kω1RC). Все это приводит к появлению линейных искажений сигнала. Таким образом, при прохождении сложного сигнала через линейные цепи искажаются его амплитуда и фаза, но при этом новые спектральные составляющие не возникают.
2.4. Спектр периодической последовательности большой cкважности
На рис. 2.10 приведена периодическая последовательность прямоугольных импульсов s(t). Длительность каждого импульса равна τи, а период их следования — Т. Скважность этой последовательности составляет q = T/ τи.
Найдем спектр последовательности импульсов. Для этого используем выражение (2.18). Рассматриваемая последовательность импульсов является четной функцией, поэтому в выражении (2.15) коэффициенты bk и аргументы θk равны нулю. Соответственно для осуществления аппроксимации последовательности импульсов необходимо вычислить коэффициенты а0/2 и ak.
Амплитуда импульсов равна А, поэтому коэффициент а0/2 будет иметь вид
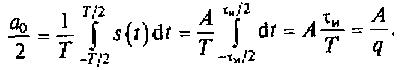
Коэффициент ak для k-й гармоники спектра сигнала можно представить следующим образом:
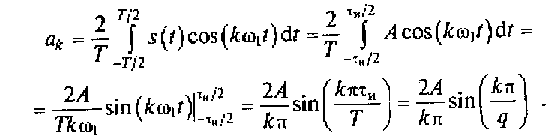
Таким образом, последовательность прямоугольных импульсов, представленная на рис. 2.10, описывается рядом Фурье (2.15), т.е.
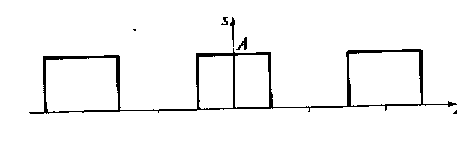
Рис. 2.10. Периодическая последовательность прямоугольных импульсов
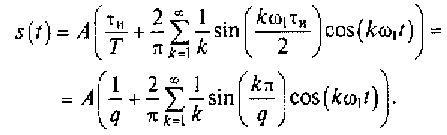
Из полученного выражения видно, что модуль k-го коэффициента
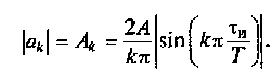
В этом выражении аргумент функции sin(kπτи /T) умножим и разделим на τи. В результате получим выражение, которое позволяет провести анализ спектра импульсной последовательности большой скважности, приведенного на рис. 2.11:
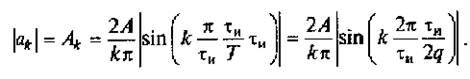(2.16)
Рассматривая выражение (2.16), можно сделать следующие выводы относительно спектра периодической последовательности импульсов.
1. Функция sin(kπτи /T) равна нулю на частотах ω = k2π/τи. Минимальная частота спектра периодической последовательности ω1 = 2π/T. Это говорит о том, что число спектральных составляющих (ω/ω1) = (kТ/ τи) = kq в диапазонах частот 0 < ω ≤ 2π/τи, 2π/τи < ω ≤ 4π/τи и т.д. Таким образом, с уменьшением длительности τи и увеличением скважности q = T/τи следования импульсов число спектральных составляющих растет, интервал между ними уменьшается, а амплитуды спектральных составляющих медленно убывают.
2. Известно, что при малых k функция sin(kπτи/Т) ≈ kπτи/T. В этом случае амплитуды гармоник спектра периодической последовательности импульсов представляются в виде
Ak ≈ (2A/ kπ) kπ (τи/ Т) = 2A/q. Таким образом, при малых k амплитуды гармоник спектра обратно пропорциональны скважности импульсной последовательности, т.е. с увеличением скважности следования импульсов амплитуды гармоник уменьшаются.
3. Из рис, 2.11 видно, что спектр периодической последовательности импульсов состоит из бесконечного множества «лепестков». расположенных в диапазонах частот 0 < ω ≤ ≤2π/τи, 2π/τи < ω ≤ 4π/τи , ..., (n – 2)π/ τи < ω ≤ nπ/τи ... . Здесь п = 1, 2, 3 ... — номер спектральной составляющей в «лепестке» спектра.
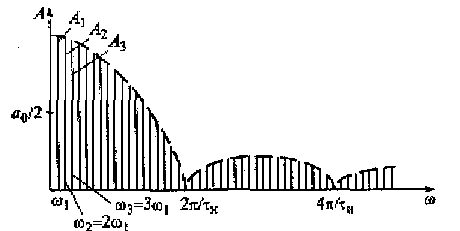
Рис. 2.11. Спектр импульсной последовательности большой скважности
Выражение (2.16) можно свести к виду
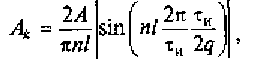
где l = 1, 2, 3 ... — номер «лепестка» спектра.
На границах частотного диапазона «лепестков»
спектра амплитуды спектральных составляющих равны нулю, а при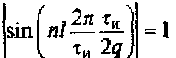 
амплитуды имеют максимальное значение Al max = 2A/(πnl). Это возможно при nl(2π/τ)(τ/2q) = lπ/2, т.е. при п = q/2. При этом максимальная амплитуда Al max = 4A/(πnl) спектральных
составляющих в «лепестке» спектра уменьшается пропорционально как номеру
«лепестка» l, так и скважности q.
4. Частотный диапазон каждого «лепестка» спектра имеет ширину
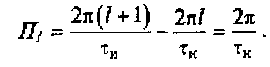
Поскольку τи = Т/q, то ширина «лепестка» спектра П1 = ω1q. Отсюда видно, что ширина спектра периодической последовательности импульсов возрастает пропорционально скважности следования импульсов.
2.5. Мощность спектра периодического сигнала
Допустим, что сигнал s(t) являющийся током или напряжением, описывается сложной периодической функцией. Энергия этого сигнала по выражению (2.2) представляет собой бесконечную величину, так как t1 = -∞, а t2 = ∞ . Для подобных сигналов большой интерес представляет оценка средней мощности
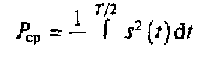за период изменения этой функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.