Сигналы и их детерминированные модели. Спектральное представление детерминированных сигналов (1, 2 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 13

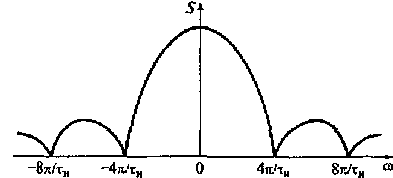
Рис. 2.18. Спектральная плотность си гна­ла, представляющего собой треугольный импульс

Из решений примеров 2.6 и 2.7 можно сделать следующие сравнительные выводы:

максимальное значение модуля спектральной плотности треу­гольного импульса (2.22) в 2 раза меньше максимального значения модуля спектральной плотности прямоугольного импульса (2.21);

ширина спектра треугольного импульса в 2 раза больше ширины спектра прямоугольного импульса при одинаковой длительности импульсов;

модуль спектральной плотности боковых «лепестков» спектра треугольного импульса убывает пропорционально 1/ω², т.е. модуль спектральной плотности боковых «лепестков» треугольного импульса снижается существенно быстрее, чем модуль спектральной плотности прямоугольного импульса.

2.7. Свойства преобразования Фурье

Для решения практических задач установим связь между спектральной плотностью сигналов (2.17) и временным описанием сигналов (2.18). Для этого рассмотрим ряд положений, характеризующих преобразования сигналов и их спектров.

Сдвиг сигналов во времени. Допустим, имеется сигнал s₁(t), который существует в пределах временного интервала [t₁, t₂]. Этому сигналу соответствует спектральная плотность (2.17).

Сдвинем сигнал  s₁(t), во времени на величину t₀, не изменив его спектральной плотности. В результате этого получим сигнал s₂(t) = s₁(t - t₀), спектральная плотность которого принимает вид:

В отношении спектральной плотности s₂(jω) сигнала s₂(t), полученного путем сдвига по оси времени сигнала s₁(t), можно отметить следующее:

спектр амплитуд S(ω) спектральной плотности остается неизменным;

фазовая характеристика спектральной плотности изменяется на ±ωt₀ ;

при добавлении к фазе каждой спектральной составляющей S₁(jω) исходного сигнала s₁(t),  фазового сдвига ±ωt₀ можно говорить, что сигнал сдвигается во времени на t₀.

Пример 2.10. Имеется последовательность (пачка) N равноотстоящих друг от друга одинаковых прямоугольных импульсов длительностью τ_и и амплитудой А (рис. 2.19). Необходимо найти спектральную плотность последовательности (пачки) импульсов.

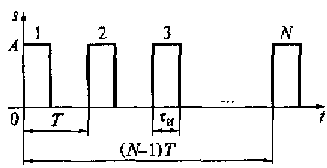
Рис. 2.19. Последовательность (пач­ки) равноотстоящих одинаковых прямоугольных импульсов

Решение. Спектральная плотность первого импульса последовательности описывается выражением (2.20), полученным в примере 2.6, а именно:

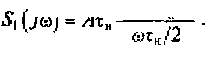
Спектральные плотности второго и последующих импульсов в пачке можно рассматривать, как спектральные плотности первого импульса с фазовыми характеристиками, измененными на величину ±ωпТ, где п =  1,2, 3, ..., N:

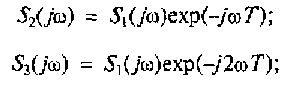
В этом случае суммарная спектральная плотность последовательности из N импульсов будет иметь вид:

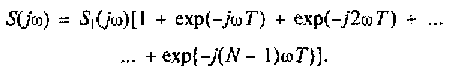
Рассматривая слагаемые данного выражения, помешенные в круглых скобках, можно сделать следующие выводы;

на частотах ω = п2π/Т где п = 1, 2, 3, ... , N- 1 каждое из слага­емых в квадратных скобках равно 1. Соответственно в окрестности этой частоты располагается спектральная плотность первого им­пульса S₁(п2π/Т);

учитывая, что в последовательности (пачке) содержится N импульсов, модуль спектральной плотности этой последователь­ности можно определить из выражения S(ω) = NS₁ (п2π/Т), в ко­тором спектральные составляющие с частотами ω = п2π/Т  скла­дываются с фазовыми сдвигами, кратными 2π. Это приводит к тому, что модуль спектральной плотности пачки импульсов в N раз больше модуля спектральной плотности одиночного импуль­са;

на частотах ω = 2π/(NТ), а также на частотах, когда сумма сла­гаемых ехр(-jkωT) в квадратных скобках обращается в нуль, сум­марная спектральная плотность пачки импульсов равна нулю;

на частотах ω = 2πN/T, отличных от ω = n2π/Т модуль спект­ральной плотности определяется геометрической суммой различ­ных спектральных плотностей отдельных импульсов при одинако­вой частоте.

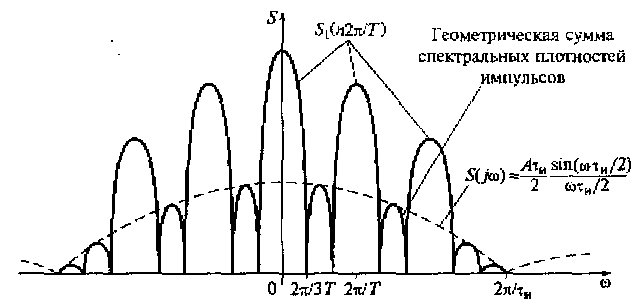
Рис. 2.20. Модуль спектральной плотности последовательности из трех равноотстоящих одинаковых прямоугольных импульсов

На рис. 2.20 приведен модуль спектральной плотности после­довательности, включающей три равноотстоящих одинаковых прямоугольных импульса длительностью τ_и и периодом следова­ния импульсов Т = 3τ_и. Пунктирной линией отмечен модуль спек­тральной плотности одиночного импульса.

Изменение масштаба времени. Допустим, имеется произвольный импульсный сигнал s₁(t), длительность которого равна τ_и (сплош­ная линия 1 на рис. 2.21). Изменив масштаб времени этого сигнала на n, получим новый сигнал s₂(t) = s₁(nt). Этому сигналу при п > 1 на рис. 2.21 соответствует пунктирная линия 2, а при п < 1 — штрихпунктирная линия 3.

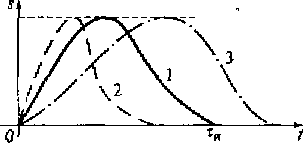
Рис. 2.21. Импульсный сигнал (1), его сжатая (2) и растянутая (3) во времени копии

Исходному сигналу s₁(t) соответствует спектральная плотность S₁(jω). Спектральная плотность сигнала, полученного при масш­табировании времени, приобретает вид

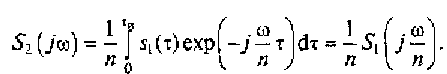
Проведенные вычисления показывают, что при сжатии на вре­менной оси сигнала в п раз его спектр на оси частот расширяется также в п раз, а амплитуды спектральных составляющих модуля спектральной плотности уменьшаются в п раз.

Напротив, при растяжении на временной оси сигнала в п раз его спектр на оси частот уменьшается, а амплитуды спектральных со­ставляющих модуля спектральной плотности увеличиваются в п раз.

Смещение спектра сигнала по оси частот. Допустим, сигнал s(t) умножен на гармоническую функцию постоянной частоты cos(ωt + Θ₀) или sin(ωt + Θ₀). Доказано, что в этом случае спектр сигна­ла расщепляется на две части, которые смешены по оси частот на –ω₀  и + ω₀. Справедливо и обратное утверждение: смещение спектра сигнала по оси частот эквивалентно умножению исход­ного сигнала на гармоническую функцию постоянной величины.