Частотные характеристики и операторные функции электрических цепей

ГЛАВА 5

Частотные характеристики и операторные функции

электрических цепей

Большинство электрических цепей служат средством связи для передачи сигналов от источника сигнала в нагрузку (рис.5.1), где x(t)- сигнал на входе цепи, он называется входным сигналом или воздействием; y(t)- выходной сигнал или отклик.

y(t)=F(x(t),a,b,c) - в общем случае, связь между откликом и воздействием имеет вид дифференциального уравнения, если цепь линейная, то уравнение линейное, где a,b,c- параметры элементов, входящих в цепь.

Если входной сигнал гармонический, то его представляют комплексной амплитудой.

→  

Если цепь линейная, то откликом такой цепи является гармонический сигнал с комплексной амплитудой .

   →  

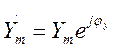Причем связь между комплексной амплитуды отклика и воздействия имеет вид линейного алгебраического уравнения:

 , 

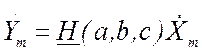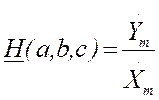
где H (a, b, c) – параметр электрической цепи (это комплексное число).

Параметр цепи есть отношение комплексной амплитуды отклика к комплексной амплитуде воздействия.

5.1. Параметры двухполюсника

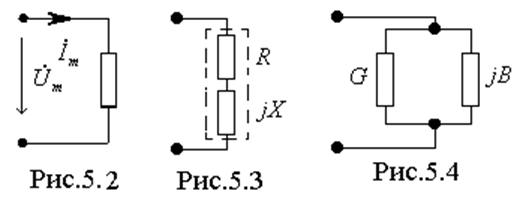
Двухполюсником является цепь с двумя выводами рис.5.2. Его режим работы характеризуется двумя величинами

1. Если воздействием считать амплитуду тока, то откликом будет являться напряжение на нем.

По закону Ома: , где Z – сопротивление двухполюсника. (Z=R+jX – комплексное число, где R и X резистивная и реактивная составляющие сопротивления двухполюсника).

Обобщенная схема замещения двухполюсника приведена на рис. 5.3.

2.Если воздействием считаем амплитуду напряжения, тогда откликом будет амплитуда тока, которая связан с напряжением:

     .

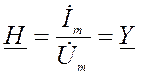, где Y- второй параметр двухполюсника, он называется комплексной проводимостью двухполюсника. Y=G+jB, где G и B резистивная и реактивная составляющие проводимости двухполюсника.   

Вторая схема замещения двухполюсника приведена на рис. 5.4. Эти схемы замещения, при определенном выборе параметров, эквивалентны.

5.2. Параметры четырехполюсника

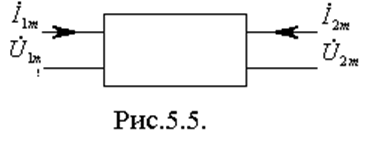Четырехполюсник – это цепь с четырьмя выводами (рис.5.5).

Параметры четырехполюсника можно разбить на четыре группы:

1.  Входные параметры связывают  и :

По отношению к источнику сигнала четырехполюсник является двухполюсником, а поэтому его входные параметры аналогичны параметрам двухполюсника:

  ,     ,

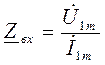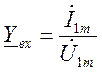где - входное сопротивление четырехполюсника; - входная проводимость четырехполюсника.

2. Передаточные параметры характеризуют передачу сигнала, со входа на выход или, как говорят, передачу в прямом направлении. Передаточных параметров четыре

;      ;       ;       ,

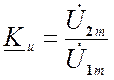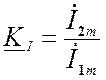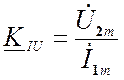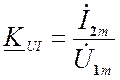где - коэффициент передачи по напряжению;

- коэффициент передачи по току;

- сопротивление прямой передачи или коэффициент преобразования ток – напряжение;

- проводимость прямой передачи или коэффициент преобразования напряжение - ток.

3. Выходные параметры:

а) 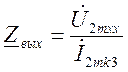, где - комплексное выходное сопротивление.

- комплексная амплитуда выходного напряжения в режиме холостого хода. (ХХ – холостой ход), это режим когда выполняются условия (, =∞)

- комплексная амплитуда выходного тока в режиме короткого замыкания. (КЗ – короткое замыкание), это режим когда ().

б) 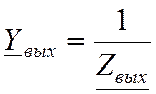 комплексная выходная проводимость.

4. Параметры обратной передачи сигнала. Они характеризуют передачу сигнала с выхода на вход. Таких параметра четыре и они аналогичны параметрам второй группы: (,,,).

5.3. Частотные характеристики

Поскольку сопротивления элементов цепей зависят от частоты, то параметры цепей оказываются частотно-зависимыми. Зависимости параметров цепей от частоты называют частотными характеристиками (ЧХ) или частотными функциями цепи.

Каждый параметр цепи имеет свою частотную характеристику ЧХ. Название ЧХ дают в соответствии с названием  параметра. Например: ЧХ входного сопротивления, ЧХ коэффициента передачи напряжения.

ЧХ есть зависимость от частоты отношения комплексной амплитуды отклика к комплексной амплитуде воздействия. Как всякую комплексную функцию ее можно записать в одной из трех форм записи: показательной, алгебраической и тригонометрической (последняя, применяется редко).

.

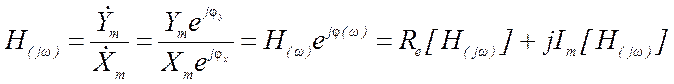H(ω)=Y_m/X_m - амплитудно-частотная характеристика (АЧХ) или ее называют модуль комплексной функции – mod[H(jω)] =.

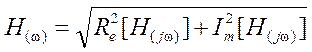АЧХ – есть зависимость от частоты отношения амплитуды гармонического сигнала на выходе к амплитуде гармонического сигнала на входе (без учета начальных фаз).

- фазо-частотная характеристика (ФЧХ) или ее называют аргументом комплексной функции – arg[H(jω)] = .

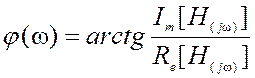ФЧХ – есть зависимость от частоты сдвига по фазе между выходным и входным сигналами.

,,- реальная и мнимая составляющие ЧХ электрической цепи.

Для наглядности ЧХ цепей представляют в виде графиков. Графики строят двумя способами.

1.  ЧХ можно представлять в виде двух графиков –АЧХ и ФЧХ.

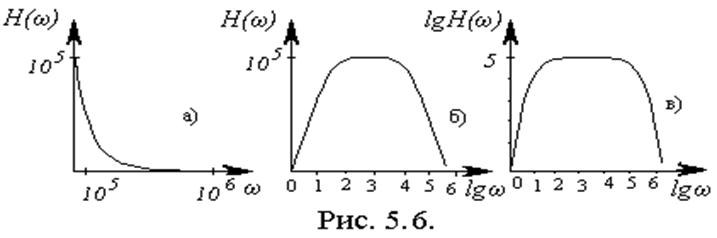
При построении графиков АЧХ и ФЧХ пользуются следующими масштабами по осям: абсолютным или линейным и логарифмическим. На рис.5.6а приведен график в абсолютном линейном масштабе, на рис.5.6б в полулогарифмическом масштабе, а на рис.5.6в в логарифмическом масштабе.

2.  ЧХ можно представить на одном графике. График комплексной функции, построенный в одной системе координат, называют годографом. Годограф – это геометрическое место точек, которые описывает конец вектора комплексной функции на комплексной плоскости при изменении частоты от 0 до бесконечности.

Для построения годографа обычно используют алгебраическую форму записи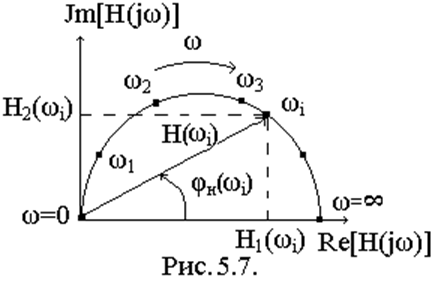 частотной характеристики Н(jω) = Re[Н(jω)] + jJm[Н(jω)]. Далее для определенных частот ω_i рассчитывают значения Re[Н(jω)] = Н₁(ω_i) и Jm[Н(jω)] = Н₂(ω_i), и составляют таблицу данных, а затем, как обычно, наносят эти точки на плоскость и соединив их получают график годографа (рис.5.7).

Таблица данных для построения АФХ                             Таблица 1.1.

5.4. Примеры расчёта частотных характеристик цепей

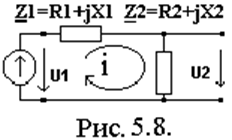
Пример 1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис.5.8) рассчитать ее частотные характеристики.

1. Z_вх(jw), Z_вх(w), j_z(w). 2. K(jw), K(w), j_k(w).

Решение. 1) По определению Z_вх(jw)=Ů_1m/.Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:

Z_вх(jw)=Ů_1m/Ĭ_1m= Ĭ_1m(Z₁+Z₂)/ Ĭ_1m =(R₁+R₂)+j(X₁+X₂)=R+jX;

Z_вх(w)=[(R₁+R₂)²+(X₁+X₂)²]^1/2;   j_z(w)=arctg[(X₁+X₂)/(R₁+R₂)].

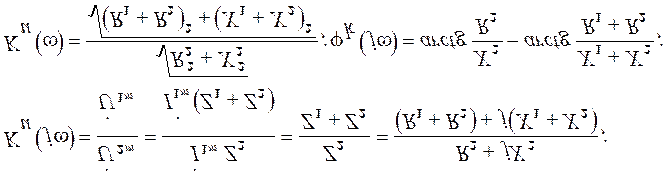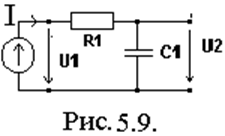
Пример 2. Для цепи изображенной на рис.5.9 рассчитать:

zвх(jw), z(w), j_z(w).

K_U(jw), K(w), j_K(w).

От исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.5.8.

Используя, определение z_вх(jw) и законы Ома и Кирхгофа получим его выражение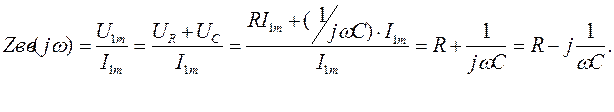

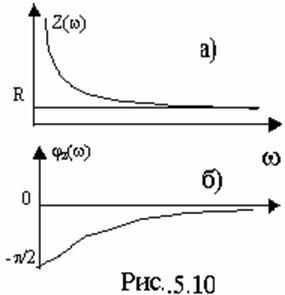
Определим АЧХ и ФЧХ для z_вх(jw) и построим их графики (рис.5.10.), подсчитав значения при w=0, w=¥.

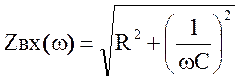;   Zвх(0) = ¥. Zвх(¥) = R.

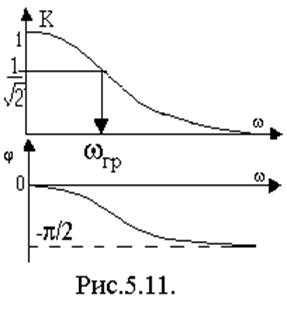j_z(w)= -arctg 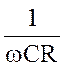,   j_z(0)=-p/2, j_z(¥)=0.